
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Газовые смеси
|
|
В практической деятельности чаще всего имеют дело не с однородными газами, а с их смесями (воздух, продукты сгорания топлива, горючие газовые смеси и т.п.). Поэтому в теплотехнике газовые смеси имеют важное значение.
В объеме, занимаемом газовой смесью, каждый газ, входящий в эту смесь, ведет себя так же, как вел бы себя при отсутствии других составляющих смеси: распространяется по всему объему; создает давление (парциальное), определяемое температурой и объемом на единицу его массы; имеет температуру смеси.
Смесь идеальных газов представляет собой идеальный газ, для которого справедливы законы и полученные для идеальных газов зависимости.
Для идеального газа давление определяется выражением (3.1):
 .
.
Количество молекул, входящих в данную смесь газов, равно сумме молекул газов, составляющих смесь:
nсм = n1 + n2 + ··· + nn. (3.63)
Произведение mw2=2aT пропорционально абсолютной температуре газа, а поскольку все газы, входящие в смесь, имеют одинаковую температуру, то справедливо равенство
2aT = m1w12 = m2 w22 = ··· = mn wn2. (3.64)
В соответствии с выражениями (3.63) и (3.64) давление для смеси газов можно представить в виде суммы


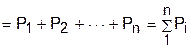 , (3.65)
, (3.65)
где Pi – парциальные давления газов, составляющих смесь.
Уравнение (3.65) представляет математическое выражение закона Дальтона (1807 г.) в соответствии с которым давление газовой смеси равно сумме парциальных давлений газов, входящих в смесь.
Парциальное давление – это давление, которое создает один из газов, составляющих смесь, при температуре смеси в случае заполнения им всего объема смеси. Парциальное давление – это реально-существующая величина, поскольку каждый отдельный газ в смеси имеет температуру смеси и занимает весь объем смеси. Парциальное давление можно определить из уравнения Менделеева –Клапейрона:
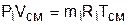 , (3.66)
, (3.66)
где Vсм – объем, занимаемый всей смесью газов;
mi – масса отдельного газа, входящего в смесь;
Ri– газовая постоянная отдельного газа;
Tсм – температура смеси газов.
Основные характеристики смеси газов
Для того чтобы воспользоваться уравнением Менделеева-Клапейрона для смеси газов
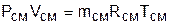 ,
, 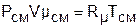 ,
, 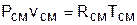 ,
,
необходимо знать газовую постоянную Rсм и молярную массу (условную) смеси µсм. Для смеси, как для любого идеального газа, эти две величины связаны соотношением Rсм=8314/µсм (Дж/(кг·К)). Чтобы рассчитать эти величины, необходимо знать состав смеси газов, т.е. какие газы и в какой пропорции входят в смесь.
Состав смеси может быть задан массовыми, объемными или мольными долями.
Массовой долей gi данного газа называется отношение его массы к массе всей смеси:
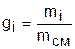 , (3.67)
, (3.67)
где mi – масса отдельного газа, входящего в смесь;
mсм – общая масса смеси.
Очевидно, что сумма массовых долей всех газов смеси равна единице:
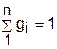 . (3.68)
. (3.68)
Объeмной долей ri данного газа называется отношение объема, который занимал бы данный газ при температуре и давлении смеси, к общему объему смеси:
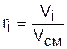 , (3.69)
, (3.69)
где Vi – объем данного газа при Тсм и Рсм, м3.
Объем Vi называют парциальным объемом, это искусственно введенная величина, поскольку каждый газ, входящий в смесь, занимает весь объем смеси. Парциальный объем можно рассчитать по уравнению Менделеева – Клапейрона:
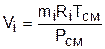 . (3.70)
. (3.70)
Записав уравнение Менделеева – Клапейрона через парциальное давление и через парциальный объем,
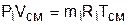 ,
,
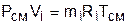 ,
,
можно получить еще одно расчетное выражение для объемной доли, поделив правые и левые части этих уравнений одно на другое:
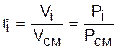 . (3.71)
. (3.71)
Поскольку сумма парциальных давлений равна давлению смеси, то сумма объемных долей всех газов смеси равна единице, а сумма парциальных объемов равна полному объему всей смеси газов:
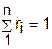 , (3.72)
, (3.72)
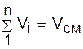 . (3.73)
. (3.73)
Для смеси газов используется понятие мольных долей. Мольной долей называется отношение количества молей данного газа Мi к общему количеству молей всех газов смеси Мсм.
Количество молей определяется делением массы газа на его молярную массу:
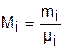 . (3.74)
. (3.74)
Воспользовавшись уравнением Менделеева – Клапейрона для парциального и полного объемов смеси газов и введя в него количество молей
 ,
,
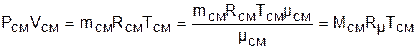 ,
,
получим еще одно расчетное выражение для мольной доли:
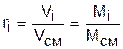 . (3.75)
. (3.75)
Равенство объемных и мольных долей для смеси газов можно получить и из закона Авогадро, в соответствии с которым объемы молей всех идеальных газов при одинаковых параметрах одинаковы, т.е. число молей при одинаковых параметрах идеальных газов прямо пропорционально полным объемам этих газов: Vmi=Vi/Мi=Vсм/Мсм=Vmсм.
Существует взаимосвязь массовых и объемных долей смеси. Ее несложно получить, выразив массы газов через произведение их объемов на плотности, а отношение плотностей при одинаковых параметрах, в соответствии с законом Авогадро, заменив отношением молекулярных масс:
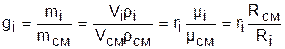 . (3.76)
. (3.76)
Уравнение (3.76) позволяет получить расчетные выражения для молярной массы и газовой постоянной смеси газов на основании равенства единице суммы массовых и объемных долей всех газов данной смеси:
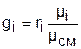 , ®
, ® 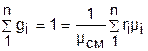 , ®
, ® 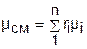 , (3.77)
, (3.77)
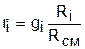 , ®
, ® 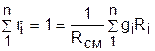 , ®
, ® 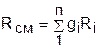 . (3.78)
. (3.78)
При известной молярной массе смеси газовую постоянную смеси проще определить из соотношения
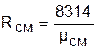 .
.
Для определения парциального давления данного газа в смеси можно воспользоваться выражением (3.71). В соответствии с ним
Pi = riPсм.
Теплоемкости газовых смесей
Полная теплоемкость смеси газов представляет собой сумму теплоемкостей газов, составляющих смесь. Это справедливо, поскольку теплота подчиняется закону суммирования (адитивности).
 . (3.79)
. (3.79)
Удельную массовую теплоемкость смеси газов можно получить, разделив выражение (3.79) на массу смеси газов и выразив полные теплоемкости каждого газа через произведение их масс на соответствующие им удельные массовые теплоемкости:
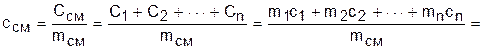

 .
.
Получили, что удельная массовая теплоемкость смеси газов равна сумме произведений массовых долей на удельные массовые теплоемкости газов, составляющих смесь:
 . (3.80)
. (3.80)
Удельную объемную теплоемкость смеси газов можно получить, разделив выражение (3.79) на объем смеси и выразив полные теплоемкости каждого газа в виде произведения их парциальных объемов на соответствующие им удельные объемные теплоемкости:

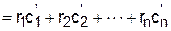 .
.
 |
Использование парциальных объемов правомерно (рис.3.4), поскольку они соответствуют массовому количеству каждого газа, входящему в смесь, т.е. количество теплоты можно представить выражением
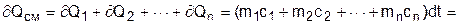
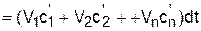 .
.
Получили, что удельная объемная теплоемкость смеси газов равна сумме произведений объемных долей на удельные объемные теплоемкости газов, составляющих смесь:
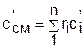 . (3.81)
. (3.81)
Удельную мольную теплоемкость смеси газов можно получить, умножив выражение (3.81) на объем одного киломоля, поскольку по закону Авогадро объем одного киломоля всех идеальных газов при одинаковых параметрах одинаков (Vmcм=Vm1=Vm2=×××=Vmn):

 .
.
Получили, что удельная мольная теплоемкость смеси газов равна сумме произведений объемных долей на удельные мольные теплоемкости газов, составляющих смесь:
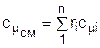 . (3.82)
. (3.82)
Для простоты запоминания расчетных выражений характеристик смеси идеальных газов можно воспользоваться следующей закономерностью: все характеристики смеси газов, которые рассчитываются в виде суммы произведений характеристик отдельных газов на их доли, имеют в расчетных выражениях массовые доли, если характеристика в знаменателе имеет единицу измерения массы килограмм (кг), во всех остальных случаях их характеристики умножаются на объемные доли.
Например, единица измерения газовой постоянной смеси Rсм (Дж/(кг×К)) – она рассчитывается в виде алгебраической суммы произведений газовых постоянных Ri на массовые доли ее компонентов gi, т.к. в знаменателе ее единицы измерения находится килограмм (кг).
Date: 2015-05-09; view: 1452; Нарушение авторских прав