
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Понятие об энтропии
|
|
Помимо внутренней энергии в термодинамике большую роль играет еще одна функция состояния, которая получила название энтропия.
Величина ΔQ/T называется приведенной теплотой. Приведенная теплота, полученная телом, равна количеству полученной теплоты, деленной на температуру тела. Уже говорилось, что подведенная к системе теплота при переходе от одного состояния в другое зависит от пути процесса, а при совершении цикла не равна нулю. С точки зрения математики это означает, что теплота не является полным дифференциалом.
В случае цикла Карно тело получает теплоту Q1 при изотермическом расширении с температурой T1 и отдает тепловую энергию Q2 при температуре T. Полная теплота, полученная телом за цикл Q1-Q2, не равна нулю. В то же время приведенное количество теплоты, полученное телом при расширении, равно Q1/T1, а при сжатии –Q2/T1 (теплообмен газа с внешними телами осуществляется только на изотермах). Оказывается, количество приведенной теплоты, полученной газом за цикл, равно нулю[4]:
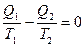 , (2.29)
, (2.29)
что означает также независимость приведенного количества теплоты от пути процесса, а только от начального и конечного состояний, т.е. является функцией состояния. Математическим языком о том же самом можно сказать, что приведенное количество теплоты является полным дифференциалом
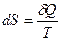 (2.30)
(2.30)
некоторой функции состояния S. Функция состояния S называется энтропией.
Из определения (2.30) следует, что если у системы в начальном состоянии {р1,V1,Т1} была энтропия S1, то при переходе в другое состояние при равновесном процессе ее энтропия будет равна:
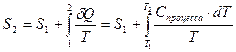 . (2.31)
. (2.31)
Пример
Определить изменение энтропии 200г воды, охлаждаемой от t1=18˚C до t2=0˚C.
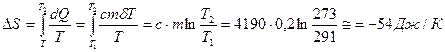 .
.
Рассмотрим некоторые свойства энтропии, следующие из определения.
· Энтропия нескольких тел равна сумме энтропий этих тел:
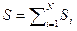 .
.
· При равновесных процессах без передачи тепла (адиабатических процессах) энтропия системы не меняется.
S=const, если ΔQ=0.
· Энтропия, как и все функции состояния, определяется с точностью до константы, поэтому измеримой величиной является только разность энтропий в начальном и конечном состояниях.
· При постоянном объеме энтропия является функцией внутренней энергии тела. Действительно, согласно первому началу термодинамики: если dV=0, то δQ=dU, следовательно
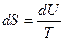 .
.
Выразим значения энтропии идеального газа через термодинамические параметры, воспользовавшись уравнениями состояния, выражением для внутренней энергии и первым началом термодинамики:
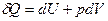 ;
; 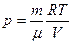 ;
; 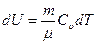 ;
;
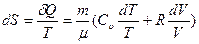 .
.
После интегрирования получим:
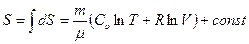 . (2.32)
. (2.32)
Это выражение позволяет найти изменение энтропии ΔS при каком-либо процессев идеальном газе. Используя уравнение состояния идеального газа и уравнение Майера (Cр-Cυ=R), можно выразить энтропию газа через давление p, что в некоторых случаях более удобно:
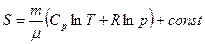 .
.
Энтропия изолированной системы. Энтропия изолированной системы при обратимых процессах остается постоянной.
Действительно, тепловая машина с нагревателем и холодильником (в частности, машина Карно) составляет изолированную систему. Энтропия системы равна сумме энтропий нагревателя Sн, газа Sг и холодильника Sx. Если передача тепла от нагревателя газу происходит при одинаковой температуре газа и нагревателя T1, то процесс теплопередачи является обратимым. То же самое справедливо для передачи тепла от газа холодильнику, имеющему температуру T2. В процессе передачи тепла Q1 газу имеем:
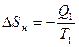 ,
, 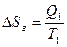 ,
, 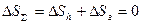 ,
,
и температура системы не меняется. Аналогичные рассуждения приводят к выводу об отсутствии изменения энтропии системы при передаче теплоты Q2 от газа холодильнику при температуре T2.
Рассмотрим теперь необратимый процесс теплопередачи в изолированной системе. Пусть два равных количества идеального газа с температурами T1 и T2 (T1<T2), содержатся в изолированных одинаковых сосудах с жесткими стенками. Если создать тепловой контакт между этими сосудами, то через некоторое время газы в сосудах придут в термодинамическое равновесие, их температуры сравняются и будут равны T=(T1+T2)/2 (из равенства количества теплоты, получаемого первым газом и отдаваемого вторым газом: Cгаза (T-T1)=Cгаза(T2-T)). Согласно (2.32), энтропия первого газа (объем газа не меняется) возрастет на:
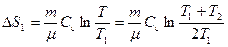 ,
,
а второго газа изменится на:
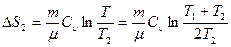 .
.
Изменение энтропии этой изолированной системы двух газов при таком процессе равно:
 ,
,
а, поскольку (Т1+Т2)>4T1T2, логарифм имеет положительное значение, следовательно, ΔSΣ>0.
Date: 2015-05-09; view: 747; Нарушение авторских прав