Теоремы подобия

В основу теории подобия физических явлений положены три теоремы. Две из них формулируют основные свойства подобных между собой явлений. Третья – обратная, устанавливает признаки подобия явлений.

Первая теорема подобия для течения двух жидкостей была сформулирована И. Ньютоном в 1686 г. Строгое ее доказательство было дано Ж. Бертраном в 1848 г.

В своем доказательстве Ж. Бертран исходил из самого общего уравнения механики, даламберова начала. Но можно за исходное уравнение взять второй закон Ньютона для 2-х механических систем:

,

.

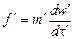Введем условия подобия 2-х систем и выразим параметры второй системы через параметры первой системы.

.

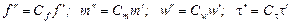Подставим полученные параметры в уравнения второй механической системы: .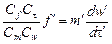

То есть, имеем два уравнения, связывающие между собой одни и те же величины, следовательно, эти уравнения тождественны и индикатор подобия будет: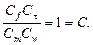

Если в индикатор подобия подставить значения констант подобия, то будем иметь

.

Полученное равенство указывает, что число подобия одинаково для всех подобных между собой явлений. Это число обозначается Ne (Ньютон).

Следовательно

.

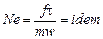Отсюда 1-я теорема формулируется следующим образом: у подобных явлений числа подобия численно одинаковы.

Вторая теорема была доказана в 1911 г. русским ученым А. Федерманом и в 1914 г. американским ученым Е. Букингемом.

Из сказанного выше видно, что для вывода чисел подобия необходимо знать функциональную связь между величинами. Если эта связь дана дифференциальным уравнением, то интегрирование его не является обязательным. Об этом говорит вторая теорема подобия, формулировка которой следующая:

Уравнением подобия называется такое уравнение, которое любую зависимость между величинами, характеризующими данное явление, представляет зависимостями между числами подобия К₁, К₂,..., К_n, или

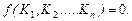
Третья теорема устанавливает условия, при которых физические явления будут подобны. Ее формулировка была дана М.В. Кирпичевым и А.А Гухманом, а доказательство теоремы – М.В. Кирпичевым в 1933 г.: подобны те явления, условия однозначности которых подобны, и числа подобия, составленные из условий однозначности, численно одинаковы.

16. ПРИМЕНЕНИЕ ТЕОРИИ ПОДОБИЯ К

КОНВЕКТИВНОМУ ТЕПЛООБМЕНУ

16.1. Приведение уравнений конвективного теплообмена

к безразмерному виду

Для практического применения теории подобия в случае конвективного теплообмена, описываемого системой дифференциальных уравнений и условиями однозначности с большим количеством переменных, необходимо, прежде всего, знать числа подобия, которые войдут в уравнения подобия.

Система дифференциальных уравнений, в которую входят дифференциальные уравнения теплообмена между твердым телом и внешней средой, энергии, или теплопроводности, в движущейся жидкости, движения вязкой несжимаемой жидкости (уравнения Навье-Стокса) и сплошности, позволяют выявить структуру чисел подобия.

Напишем указанные дифференциальные уравнения конвективного теплообмена для двух подобных систем.

Для первой системы уравнение Навье-Стокса (ось х):

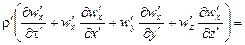
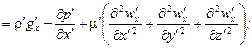(16.1)

уравнение сплошности для несжимаемой

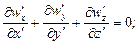(16.2)

уравнение энергии потока жидкости

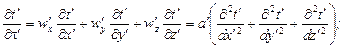(16.3)

дифференциальное уравнение теплообмена на границе твердого тела и жидкости

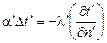. (16.4)

Аналогичные уравнения запишем для второй подобной системы:

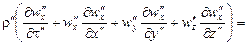
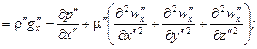(16.5)

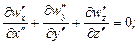(16.6)

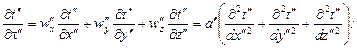(16.7)

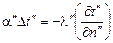. (16.8)

На основании подобия процессов сходственные величины (параметры) для обеих систем связаны попарно множителями подобного преобразования:

.

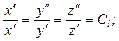
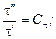
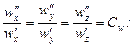
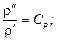
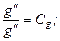
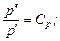
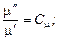
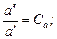
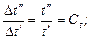
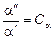Выразим все переменные в уравнениях для второй системы (с двумя штрихами) через переменные первой системы (с одним штрихом) и множители подобного преобразования и подставим их в уравнения, записанные для второй системы. После преобразований получим следующую систему:

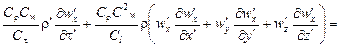
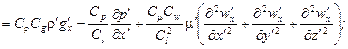(16.9)

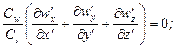(16.10)

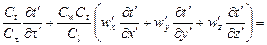
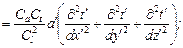(16.11)

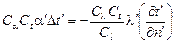. (16.12)

В результате преобразований обе подобные системы выражены через переменные первой системы. В каждую систему входят одни и те же переменные, которые определяются одинаковым образом. Это возможно только в случае тождественности уравнений первой системы (16.1)-(16.4) и уравнений полученной системы (16.9)-(16.12). Из условий тождественности уравнений следует, что комплексы, составленные из множителей подобного преобразования, должны быть равны между собой:

.

Группируя члены этого соотношения по два, получим:

; ;

;

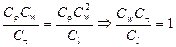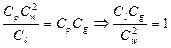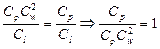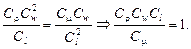
Если в последних соотношениях вместо множителей подобного преобразования подставить их значения и сгруппировать по индексам, то получим следующие числа подобия:

; ; ;

,

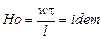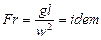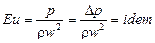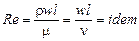где 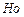– число подобия гидродинамической гомохронности, характеризующее скорость изменения поля скоростей движущейся жидкости во времени; 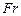- число Фруда, определяющее отношение сил инерции к силам тяжести; 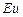- число Эйлера, характризующее соотношение между силами давления и силами инерции; Re – число Рейнольдса, представляющее собой отношение сил инерции к силам вязкости и определяющее характер движения жидкости.

Числа подобия 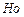, , 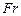, 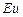Re применяют при изучении гидродинамического подобия двух или нескольких систем. Для любых сходственных точек они имеют одинаковые значения.

Из уравнений энергии потока (16.3) и (16.11) получаем следующие соотношения:

; .

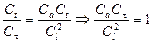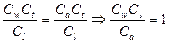Если в последних соотношениях вместо множителей подобного преобразования подставить их значения и сгруппировать по индексам, то получим следующие числа подобия:

; ,

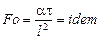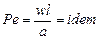где 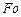- число Фурье – число тепловой гомохронности, характеризующее соотношение между скоростью изменения температурного поля, физическими параметрами и размерами тела; 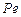- число Пекле, число подобия конвективного теплообмена.

Если в число 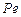вместо коэффициента температуропроводности подставить его значение 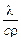, и умножить числитель и знаменатель на избыточную температуру 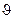, то получим 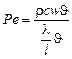, т.е. числитель дроби характеризует теплоту, переносимую конвекцией, а знаменатель – теплоту, переносимую теплопроводностью.

Далее из уравнений теплообмена (16.4) и (16.12) получим следующее соотношение множителей подобного преобразования:

.

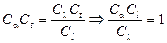После подстановки значений множителей подобного преобразования и разделения переменных найдем: ,

где 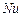- число Нуссельта, характеризующее конвективный теплообмен между жидкостью и поверхностью твердого тела.

Числа 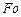, 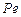и 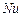применяют при изучении теплового подобия двух или нескольких систем.

Из соотношений полученных чисел можно получить другие характерные числа подобия. Так, например, разделив число 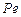на число 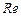, получим другое число подобия :

,

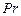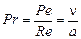где 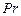- число Прандтля, определяющее физические свойства жидкости.

При изучении теплообмена в свободном потоке жидкости (естественная конвекция) учитывается число Фруда 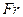, при этом используется число :

,

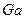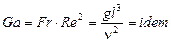где 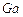- число Галилея, характеризующее соотношение сил тяжести и сил молекулярного трения (вязкости).

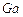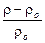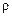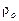Умножая число на симплекс (здесь и - плотности жидкости в двух точках потока), получим новое число :

,

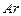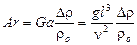где 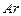- число Архимеда, определяющее условия свободного движения среды.

Для случая, когда движение жидкости определяется различием плотности среды в различных ее точках вследствие, например, разности температур в этих точках, когда 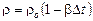, где 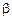- температурный коэффициент объемного расширения текущей среды (для газа 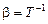), от числа Архимеда переходим к числу :

,

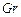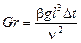где 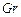- число Грасгофа, характеризующее соотношение подъемной силы, возникающей вследствие разности плотностей и сил молекулярного трения (вязкости).

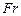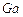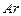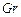Числа , , и тождественны – это четыре вида одного и того же числа.

Date: 2015-05-09; view: 1045; Нарушение авторских прав