Дифференциальное уравнение теплообмена

В процессе конвективного теплообмена характер течения жидкости имеет большое значение, так как им определяется механизм теплоотдачи. Процесс переноса теплоты на границе с твердой поверхностью может быть выражен законом Фурье

.

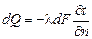Это же количество теплоты можно выразить уравнением Ньютона-Рихмана

.

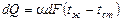Приравнивая эти уравнения, получим для коэффициента теплоотдачи

.

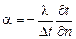Полученное уравнение описывает процесс теплообмена на поверхности канала ().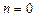

По своему физическому характеру конвективный теплообмен является весьма сложным процессом и зависит от большого числа факторов, определяющих процесс теплоотдачи. В общем случае коэффициент теплоотдачи является функцией параметров жидкости, формы и размеров твердой поверхности и др. В общем случае для коэффициента теплопроводности можно записать следующую функцию

,

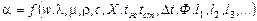где 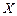- характер движения жидкости (свободное или вынужденное), Ф –форма стенки, 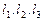- размеры поверхности.

Приведенная функция показывает, что коэффициент теплоотдачи – величина сложная, и для ее определения невозможно дать общую расчетную формулу. Обычно для определения 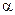используют экспериментальные данные.

Применяя законы физики, можно составить соответствующие дифференциальные уравнения для конвективного теплообмена, учитывающие как тепловые, так и динамические явления в любом процессе. Эта система дифференциальных уравнений должна включать уравнения энергии (теплопроводности), теплообмена, движения и неразрывности потока (уравнения сплошности).

1. Дифференциальное уравнение энергии устанавливает связь между пространственным и временным изменением температуры в любой точке движущейся жидкости:

.

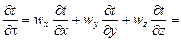
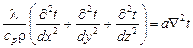Если w_x = w_y = w_z = 0, то уравнение энергии переходит в уравнение теплопроводности для твердых тел (при условии отсутствия внутренних источников теплоты).

2. Дифференциальное уравнение теплообмена выражает условия теплообмена на границе твердого тела и жидкости:

.

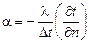Полученная формула для коэффициента теплоотдачи выражает условия теплообмена на границе твердой стенки и жидкости.

3. Дифференциальные уравнения движения вязкой несжимаемой жидкости (Навье-Стокса):

для оси х –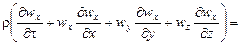

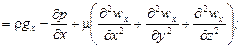
для оси y –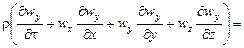

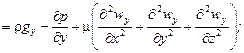
для оси z –

.

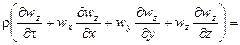
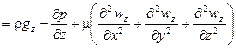4. Дифференциальное уравнение сплошности, или неразрывности потока:

для сжимаемых жидкостей –

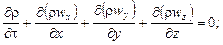
для несжимаемых жидкостей (при r = const) –

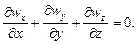
Date: 2015-05-09; view: 1321; Нарушение авторских прав