Основы теории подобия

При изучении физических явлений применяют два метода исследований, позволяющие получить количественные закономерности для явлений.

1 – экспериментальный метод,

2 – теоретический метод.

При экспериментальном методе получают достоверные результаты и, крое того, численные значения наиболее необходимых для практических целей величин. Основной недостаток экспериментального метода – ограниченность условий возможного использования полученных закономерностей.

Теоретический метод позволяет обосновать закономерности практически на всю возможную область их применения. Для этого составляются дифференциальные уравнения, которые описывают самые общие законы природы, которые, в свою очередь являются обобщением опытных данных.

То есть любое дифференциальное уравнение является математической моделью целого класса явлений. Под классом понимается совокупность явлений, характеризующихся одинаковым механизмом процессов и одинаковой природой.

Явления, которые входят в класс подчиняются одинаковым уравнениям, как по форме, так и по физическому содержанию.

Например, дифференциальное уравнение теплопроводности 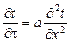- описывает целый класс явлений нестационарной теплопроводности, которые имеют одинаковый механизм процессов.

Можно записать дифференциальное уравнение нестационарного процесса переноса вещества (закон Фурье) в виде 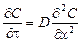, где D – коэффициент диффузии; С – концентрация вещества.

Эти уравнения одинаковые по форме, но описывают различные классы явлений, так как величины, входящие в них, имеют различное физическое содержание. При интегрировании дифференциальных уравнений можно получить бесчисленное множество решений, удовлетворяющих этому уравнению. Чтобы получить из –множества решений одно частное, надо знать все характерные особенности явления, выделяющие его из всего класса однородных явлений. Эти дополнительные условия, которые вместе с дифференциальным уравнением однозначно определяют единичное явление, называются условиями однозначности.

Условия однозначности характеризуются следующими признаками:

1.Геометрические условия, характеризующие форму и размеры тела или системы;

2. Физические условия;

3. Граничные условия, характеризующие взаимодействие системы с окружающей средой (условия протекания процессов);

4. Временные условия, характеризующие протекание процесса в начальный момент времени по всему объему системы (для стационарных процессов временные условия отпадают).

Дифференциальное уравнение и четыре условия однозначности определяют конкретное единичное условие.

Однако, в большинстве случаев и, в частности, в случае описания конвективного теплообмена из-за сложности изучаемых явлений найти решение, удовлетворяющее условиям однозначности и дифференциальному уравнению невозможно. Следовательно – недостатком теоретического метода (математической модели), является невозможность перейти от класса явлений к единичному конкретному явлению.

Если положительные стороны математического и экспериментального метода объединить в одно целое, то получим универсальный аппарат для изучения различных явлений природы. Такое объединение обоих методов осуществляется теорией подобия.

Числа подобия. При изучении явлений, одинаковой физической природы, но протекающих в различных условиях используются методы физического и геометрического подобия, характеристикой которого являются числа подобия (константы подобия).

Пусть длины двух отрезков 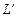и 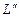связаны между собой константой геометрического подобия С _L. Если взять части этих отрезков 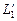и 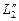, отвечающие константе С_L, то

.

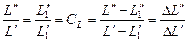Перейдя к пределу, получим ,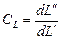

то есть, константа подобия определяет связь как конечных, так и бесконечно малых приращений системы.

Правило выбора констант подобия. Рассмотрим на примере дифференциального уравнения теплообмена, которое запишем для сходственных точек двух подобных систем.

Для первой системы: ;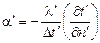

для второй системы: . (*)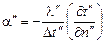

Введем константы подобия

,

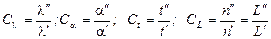где L – характерный размер системы.

Из определения констант подобия следует, что

.

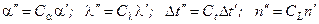Подставим эти выражения в (*) и, после сокращения на С_t, получим

(**)

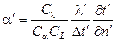Уравнения (*) и (**) тождественны, так как выражают связь между параметрами процесса, обусловленную одним дифференциальным уравнением для 1-ой и 2-ой системы. Из условия тождественности следует, что 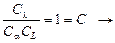связь между константами подобия.

Таким образом, выбор комплекса констант подобия ограничен условием: любая их комбинация должна быть равна 1. Величину С называют индикатором подобия.

.

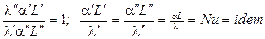Следовательно, существуют такие безразмерные соотношения параметров, характеризующих процесс, которые у подобных явлений в сходственных точках имеют численно одинаковые значения. Эти безразмерные соотношения называют числами подобия. Полученное выше соотношение (Nu) называют числом Нуссельта.

Date: 2015-05-09; view: 782; Нарушение авторских прав