Теплопроводность через многослойную цилиндрическую

Стенку

Для вывода расчетных формул рассмотрим трехслойную цилиндрическую стенку с температурами внутренней и внешней поверхностей, соответственно, 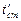и 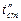. Коэффициенты теплопроводности слоев - 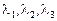, а диаметры - . Температуры каждого слоя изменяются по логарифмическому закону, а общая температурная кривая имеет вид ломаной логарифмической кривой. При стационарном режиме теплопроводности через слои цилиндрической стенки проходит один и тот же тепловой поток и для каждого из слоев будем иметь

, , .

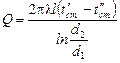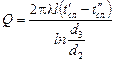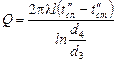Решая полученные уравнения относительно разности температур и почленно складывая, получим

+

^{___________________________________________}

,

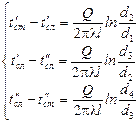
откуда получим

.

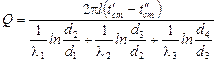Для n слоев цилиндрической стенки формула теплового потока будет иметь вид

.

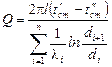Вводя в уравнение теплового потока коэффициент эквивалентной теплопроводности, получим

,

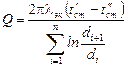где коэффициент эквивалентной теплопроводности определяется также как и для плоской многослойной стенки

.

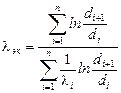Температура между слоями цилиндрической стенки:

, ,

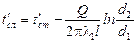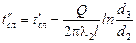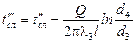
и т.д.

13.7. Теплопроводность через шаровую стенку

Постоянный тепловой поток направлен через шаровую стенку, причем источник теплоты находится внутри шара. Температура изменяется только по направлению радиуса. Изотермические поверхности представляют собой концентрические шаровые поверхности. Температура внутренней поверхности 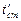, наружной 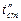, теплопроводность стенки l постоянна; внутренний радиус шара 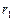, наружной - .

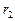Тепловой поток, проходящий через шаровой слой радиусом r и толщиной dr, находим из уравнения Фурье:

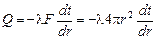или .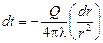

Интегрируем последнее уравнение по t и r. Постоянную интегрирования находим из граничных условий 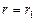при , при 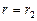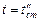. В итоге получим:

.

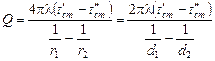Date: 2015-05-09; view: 797; Нарушение авторских прав