Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






Дифракция света

⇐ ПредыдущаяСтр 10 из 18Следующая ⇒

 

Дифракция – это явление отклонения световых волн от прямолинейного распространения при встрече с препятствием или экраном, имеющим отверстие.

Дифракция в сходящихся лучах (дифракция Френеля) – это дифракция сферических волн, осуществляемая в том случае, когда дифракционная картина наблюдается на конечном расстоянии от препятствия, вызвавшего дифракцию.

Дифракция в параллельных лучах (дифракция Фраунгофера) наблюдается в том случае, когда источник и точка наблюдения бесконечно удалены от препятствия, вызывающего дифракцию.

В задачах, связанных с дифракцией света, используется теория Френеля – Гюйгенса. Согласно этой теории, любая точка пространства, до которой дошел фронт волны, представляет собой вторичный источник. Все вторичные источники когерентны.Наблюдаемое распределение интенсивности есть результат интерференции вторичных волн.

Аналитическое выражение принципа Гюйгенса – Френеля, для амплитуды результирующего колебания в точке Р, удаленной на расстоянии r от волнового фронта:

 

a
f
 
S
p
 
E = ò K () rcos (w t − kr +a 0) dS, (5.1)где w t +a 0 – фаза колебания в месте расположения элемента волновой поверхности dS;

k =l – волновое число; l – длина световой волны; a0 – множитель, определяемый амплитудой светового колебания в том месте, где находится элемент поверхности dS;

 

 


                           
   
f
 
ï
 
 
   
k
 
   
=
   
S
   
.
 
   
1234

ì K () ® maxпри f = 0

í
p
f
î
ï K ()= 0при f = 2 –коэффициент,зависящийотугла j междунормалью


 

n
r к


 

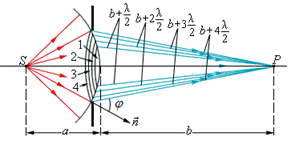площадке dS и радиус – вектора r. В теории Френеля предполагается, что фиктивные источники излучают только в направлении

внешней нормали n.

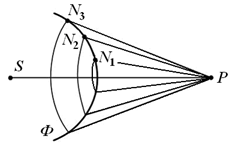
Для качественного анализа дифракционной картины используется метод зон Френеля. Фронт волны огибающей препятствие, разбивается на кольцевые зоны, так чтобы расстояния от краев зоны до Р отличалисьнаl 2 (рис. 21). Возбуждаемые

 

Рис.21
этими зонами колебания находятся в противофазе(d = p), поэтому волны от любых двух соседних зон почти гасят друг друга.

 

Радиусы зон Френеля для сферической поверхности световой волны, испускаемой точечным изотропным источником S, вычисляются по формуле

 


 

k
r =

Ab

 

a + b


 

, (5.2)


 

k
где r – радиус внешней границы k – й зоны, k – номер зоны Френеля, a – расстояние

 

диафрагмы с круглым отверстием от точечного источника света S, b – расстояние от диафрагмы до экрана, на котором ведется наблюдение интерференционной картины, l – длина волны.

 

Для плоской волны k – й зоны:

 

k
r = bk. (5.3)

 


Все зоны имеют примерно одинаковую площадь, не зависящую Френеля:

pl ab

 

a + b

Суммарная амплитуда в точке наблюдения Р: A = A–A + A–A +...

 

Выражение (5.5) при k1 можно записать в следующем виде:


от k номера зоны

 

 

(5.4)

 

 

(5.5)


 

AAAA
AAAA
ç ÷ ç ÷
24
22222222
è ø è ø
A = 1 +æ 1 − A + 3 ö+æ 3 − A + 5 ö+... = 1 ± k = 1. (5.6)

 

1442443 1442443 = 0 = 0

 

Выражения в скобках равны нулю, т.к. волны от любых двух соседних зон почти гасят друг друга.

Амплитуда открытого волнового фронта:

 

 
 
A = A. (5.7)

 

Амплитуда k – й зоны, записанная через амплитуды соседних зон:

 

AA
k
 
A = k − 1 + k + 1. (5.8)

 

−
Дифракция на круглом отверстии. Интенсивность в точке Р дифракционной картины зависит от числа зон Френеля, укладывающихся в отверстии. Если в отверстии укладывается четное число k зон Френеля, то в точке Р наблюдается минимум дифракции:

A
1k
 
A» A2A < 2. (5.9)

 


 
 
+

Если в отверстии укладывается наблюдается максимум дифракции:


A
1k
 
A» A2A < 2.

 

Дифракция на диске. Если диск

колебаний в точке Р:


нечетное число k зон Френеля, то в точке Р

 

 

(5.10)

 

закрываетпервые k зон Френеля, то амплитуда


 

A
 
A = k + 1. (5.11)

 

В точке Р всегда наблюдается дифракционный максимум, соответствующий половине действия 1 – й открытой зоны Френеля.

Дифракция на одной щели. Распределение освещенности на экране определяется углом f, отсчитанным от нормали к плоскости щели. Если щель по ширине разбить на зоны Френеля в виде полосок, разность хода, от краев которых равна /2, то число зон Френеля, укладывающихся в щели, равно:

 

∆
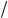
k =l 2 = l, k = 1,2,3 … (5.12)где b – ширина щели, f – угол дифракции, l – длина световой волны.

Результат интерференции света в точке Р будет зависеть от числа зон укладывающихся

в щели. Если число зон Френеля четное, то наблюдается дифракционный минимум

 
bsin f= ± 2k l, k = 1,2,3 … (5.13)

 

Если число зон Френеля нечетное, то в точке Р наблюдается дифракционный максимум

 

bsin f = ± (2k + 1)2, k = 1,2,3 … (5.14) Распределение интенсивности света на экране в зависимости от угла дифракции

называется дифракционным спектром.

 

Положение дифракционных максимумов зависит от. При освещении щели белым светом, центральный максимум наблюдается в виде белой полоски – он общий для всех. Боковые максимумы радужно окрашены фиолетовым краем к центру дифракционной

картины. Полное гашение света не происходит ни в одной точке экрана, т.к. максимумы и минимумы света с разными l перекрываются.

 

При уменьшении ширины щели ширина центрального максимума возрастает. При b £ l освещенность экрана монотонно убывает от середины к его краям. При b на

 

экране наблюдается четкое изображение источника света, образуемое по законам геометрической оптики.

Дифракция на одномерной дифракционной решетке.

Одномерная дифракционная решетка – это система параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками.

Постоянная (период) дифракционной решетки:

 

l
d = a + b = N, (5.15) где N – число щелей приходящихся на единицу длины l дифракционной решетки; a – ширина непрозрачных участков между щелями, b – ширина щелей.

Дифракционная картина от решетки является результатом дифракции волн на каждой щели и интерференции волн от различных щелей. Разности хода лучей, идущих от двух соседних щелей, будут для данного направления f одинаковы в пределах всей дифракционной решетки:

 

∆ = dsin f. (5.16)

 


 

Разность фаз двух соседних щелей определяется формулой (4.5).

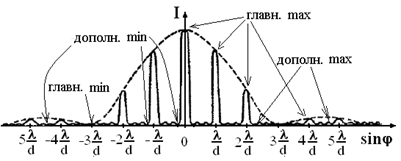
Распределение интенсивности в зависимости от угла f в спектре дифракционной решетки имеет сложный немонотонный характер (рис. 22). Различают:

главные максимумы, главные Рис.22

минимумы, дополнительные

максимумы, дополнительные минимумы интенсивности.

При нормальном падении света на дифракционную решетку положение главных максимумов определяетсяугламиотклонениялучейf, отсчитанными от нормали к плоскости решетки и выражаемые формулой


 

d × sin = ± k l, k = 0,1,2,3 … (5.17)

 

где k – порядок главного максимума.

Положение главных минимумов интенсивности в дифракционном спектре находится из условия:

 

dsin f = ± (2k + 1)2, k = 1,2,3 … (5.18) где k – порядок главного минимума.

æ ö
Между двумя главными максимумами располагается N – 1 дополнительных минимумов, разделенных дополнительными максимумами, создающими слабый фон. Условие дополнительных минимумов интенсивности:

ç ÷
N
dsin = è k ± 1 øl, k = 0,1,2,3 … (5.19) где k – порядок главного максимума.

l
Угловая ширина центрального максимума определяется через положение дополнительных минимумов (5.19) при k0:

 

f
f
2 = ± 2arcsindN» ± 2dN. (5.20) При увеличении N уменьшается угловая ширина центрального максимума 2, острота

 

главного максимума возрастает, также возрастает число темных полос. Светлые полосы будут более узкие и яркие, в тоже время промежутки между ними будут темнее. Увеличивается контрастность дифракционного спектра.

Дифракция на трехмерной дифракционной решетке.

При дифракции рентгеновских лучей на кристаллической решетке направления, в которых имеет место зеркальное отражение (дифракционный максимум), определяется из уравнения Вульфа – Брэггов:

2d × sin q = ± k l, k = 0,1,2,3 … (5.21)где d– расстояние между атомными плоскостями кристалла, q – угол скольжения (угол

 

между направлением пучка параллельных лучей, падающих на кристалл, и гранью кристалла).

Характеристики спектрального прибора. Разрешающая способность спектрального прибора

l
∆
R = l, (5.22)

 

где ∆l – минимальная разность длин волн (l 1= l, l 2= l + ∆l) двух спектральных линий, при которой эти линии могут восприниматься раздельно.

 

 


 
 
∆


Разрешающая способность дифракционной решетки

R=k × N. (5.23) Угловая дисперсия:

D
∆
f=∆l, (5.24)где ∆f – угловое расстояние между спектральными линиями, отличающимися по длине

 

волнына ∆l.

 

Угловая дисперсия дифракционной решетки

 

k
f
D = d × cos, (5.25)

 


где k – порядок спектра, d– период дифракционной решетки. Линейная дисперсия дифракционной решетки

 

l
D
l = ∆l,

где∆ l – линейное расстояние на экране между спектральными линиями, длиневолнына ∆l.


 

(5.26)

 

отличающимися по


 

Решение тестовых задач раздела «Дифракция света»

Тест 1

В отверстии укладывается 3 зоны Френеля. Амплитуды колебаний, создаваемые зонами равнысоответственно А1, А2, А3. Результирующая амплитуда колебаний в центре экрана равна …


 

AA
AA
33
11
AA
AA
А) 1 − 3 Б) 1 + 3 В) 2 − 2 Г) 2 + 2 Решение:

AAA
111
ç ÷
 
222222
è ø
Результирующую амплитуду колебаний в центре экрана определим по формуле (5.6): A = A +æ A − A + 3 ö+ 3 = A + 3.

1442443 = 0

 

Ответ: Г.

 

Тест 2

На рисунке 23 представлена схема разбиения волновой поверхности Ф на зоны Френеля. Разность хода между лучами N3P и N1P равна …

 
 
А) 1 l Б) 3 l В) Г) 2 l Рис.23

 

Решение:

 
Фронтволны Ф, разбивается на кольцевые зоны, так чтобы расстояния от краев зоны доточки Р отличалисьна∆= k l,где k = 1,2,3 …Оптическаяразностьходамеждулучами

 

 

l
N3P и N1P при k = 2 равна: ∆ = 22 = l. Ответ: В.

 

Тест 3

Рис.24а
На диафрагму с круглым отверстием радиусом 1 мм падает нормально параллельный пучок света длиной волны 0,5 мкм(рис.

24а). На пути лучей, прошедших через отверстие, на расстоянии 1 м помещают экран. В центре экрана в точке M будет наблюдаться …

 


 

А) темное пятно, так как в отверстии укладывается 4 зоны Френеля Б) светлое пятно, так как в отверстии укладывается 3 зоны Френеля В) темное пятно, так как в отверстии укладывается 2 зоны Френеля Г) светлое пятно, так как в отверстии укладывается 5 зон Френеля

 

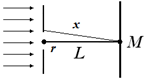Решение:

Рис.24б
Интенсивность в точке М дифракционной картины зависит от числа зон Френеля, укладывающихся в отверстии. Если в отверстии укладывается четное число k зон Френеля, то в точке М наблюдается минимум дифракции; если нечетное число k, то в точке М – максимум дифракции.

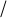Определим число открытых зон Френеля k укладывающихся в отверстие диафрагмы радиуса r. Расстояния от соседних зон Френеля до точки наблюдения должны отличаться на 2. Следовательно, расстояние от точки М до крайней точки отверстия (рис. 24б) будет

 

 
ç ÷
24
è ø
l
равно x = L + k2. Воспользуемся теоремой Пифагора: r2 =æ L + k l ö 2 − L = Lk l+ k2 l 2. Учтем, что 2 – величина второго порядка малости по сравнению с l, и пренебрежем

r
22

()
слагаемым k24. Тогда k = L.

 

1 × 10
− 32

 

Выполнимрасчет: k = 1 × 0,5 × 10 − 6 = 2. Вотверстииукладывается четное число k зон

 

Френеля, в точке М наблюдается минимум дифракции. Ответ: В.

 

Тест 4

Наибольший порядок спектра, полученный с помощью дифракционной решетки с постоянной d=5 мкмиосвещенноймонохроматическимсветомсдлинойволныl = 520 нм,

 

равен...

А) 10 Б) 9 В) 9,6 Г) 19

 

Решение:

При падении света на дифракционную решетку положение главных максимумов определяетсяугламиотклоненияf, отсчитанными от нормали к плоскости решетки, и выражается формулой (5.17): d × sin f = ± k l. Наибольший порядок спектра наблюдается,

 

когда света падает по нормали на дифракционную решетку, т.е. при sin = 1, Þ k = d.

 

5 × 10
− 6

Выполнимрасчет: k = 520 × 10 − 9 = 9,61. Порядокдифракцииможетиметь толькоцелое значение, поэтому дробную часть отбросим.

Ответ: Б.

 

Тест 5

Дифракционная решетка освещается зеленым светом. При освещении решетки красным светом картина дифракционного спектра на экране …

А) исчезнет Б) не изменится В) сузится Г) расширится

 

Решение:

 
При падении света на дифракционную решетку положение главных максимумов дифракционного спектра определяется углами отклонения f, отсчитанными от нормали к плоскостирешетки,ивыражается формулой (5.17): d × sin f = ± k l, т.е. sin f l.

 

кр > l зел, поэтому углы отклонения лучей кр >f зел. При замене освещения: зеленого цвета

 


 

на красный, картина дифракционного спектра на экране расширится. Ответ: Г.

 

Тест 6

Имеются 4 решетки с различными постоянными d, освещаемые одним и тем же монохроматическим излучением различной интенсивности. Какой рисунок иллюстрирует положение главных максимумов, создаваемых дифракционной решеткой с наименьшей постояннойрешетки? (J – интенсивность света, j – угол дифракции).

 

 

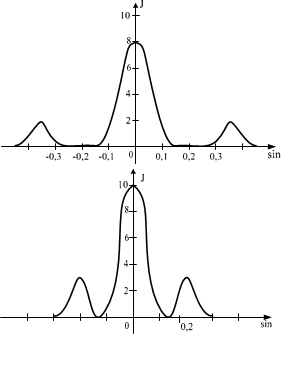
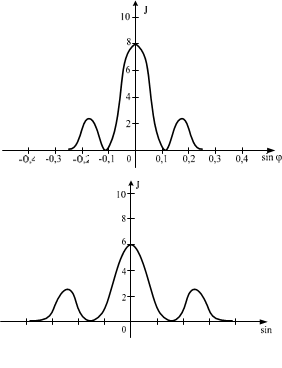А) Б)

 

 

В) Г)Д) нет правильного

 

Решение:

При наименьшей постоянной дифракционной решетки (периода) d острота главного максимума возрастает. Светлые полосы будут более узкие и яркие, в тоже время промежутки между ними будут темнее. Увеличивается контрастность дифракционного спектра. Наиболее отчетливая дифракционная картина с контрастными минимумами интенсивности первого порядка представлена на рисунке А.

Ответ: А.

 

Тест 7

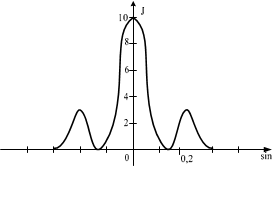
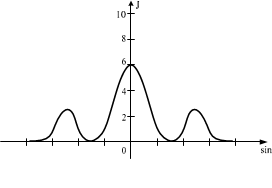
Одна и та же дифракционная решетка освещается различными монохроматическими излучениями с разными интенсивностями. Какой рисунок соответствует случаю освещения светомс наибольшей длиной волны? (J – интенсивность света, j – угол дифракции).

 

 

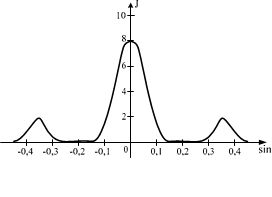
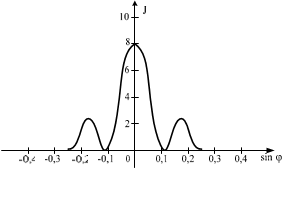А) Б)

 

 


 

 

В) Г) Д) нет правильного

 

Решение:

 
При падении света на дифракционную решетку положение главных максимумов дифракционногоспектраопределяетсяугламиотклоненияf, отсчитанными от нормали к плоскости решетки, и выражается формулой (5.17): d × sin f = ± k l, т.е. sin f l.

 

При освещении светом дифракционной решетки с наибольшей длиной волны, главные максимумыпервого порядка будут отклонены на максимальный угол f.

 

Ответ: А.

 

Тест 8

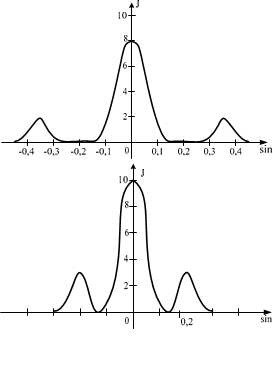
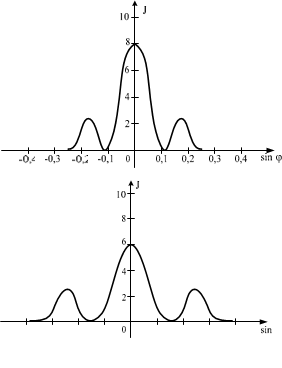
Имеются 4 решетки с различными постоянными d, освещаемые одним и тем же монохроматическим излучением различной интенсивности. Какой рисунок иллюстрирует положение главных максимумов, создаваемых дифракционной решеткой с наименьшим числом штрихов на единицу длины? (J – интенсивность света, j – угол дифракции).

 

 

А) Б)

 

 

В) Г)Д) нет правильного

 

Решение:

Приуменьшениичислаштрихов N на единицу длины дифракционной решетки увеличиваетсяеепериод d. Увеличивается угловая ширина центрального максимума 2 и

 

уменьшается его острота. Светлые полосы будут более широкие, промежутки между ними (минимумы) будут плохо различимы (почти сливаться с максимумами). Контрастность дифракционного спектра уменьшится.

Ответ: Б.

 


                       
 
 
 
 
   
−
 
 
   
+
 
 
 


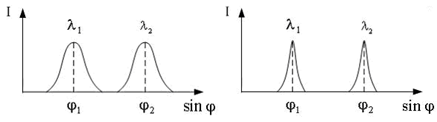Тест 9

Свет от некоторого источника представляет собой две плоские монохроматические волнысдлинамиl 1 и l 2.

 

а б
Рис.25
Имеется две дифракционные решетки с числом щелей N1 и N2, и

постояннымирешетки d1 и d2 соответственно. При нормальном падении света на дифракционную решетку 1 получено изображение максимумов, показанное на рисунке 25а. После того, как дифракционную решетку 1 поменяли на решетку 2, изображение максимумов стало таким, как показано на рисунке 25б. Постоянные решетки и число щелей этих решеток соотносятся следующим образом …

А) N1 > N2;d2 = d1 Б) N2N1;d2 > d1 В) N2 > N1;d2 = d1 Г) N2 = N1;d2 < d1

 

Решение:

21
В дифракционном спектре (рис. 25б) максимумы более острые, следовательно, разрешающая способность второй решетки R выше, чем у первой R. Разрешающая

 

21
способностьдифракционнойрешеткиопределяетсясогласноформуле(5.23): R=k × N,т.е. RN. Т.к. R > R, то N2 > N1.

При нормальном падении света на решетки длины волн 1 и l 2 видны под одинаковыми углами f 1 и 2 в обоих спектрах, следовательно, угловая дисперсия (5.25)

 

f
d
решетокодинакова D = k,Þпостоянныерешетокбудут тоже равны d2 = d1. Ответ: В.

Тесты для самостоятельного решения по разделу «Дифракция света»

 

⇐ Предыдущая567891011121314Следующая ⇒





Date: 2015-05-09; view: 2824; Нарушение авторских прав


mydocx.ru - 2015-2024 year. (0.136 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию