Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Интерференция света
|
|
Интерференцией света называется явление наложения двух (или нескольких) когерентных световых волн, в результате которого в одних местах возникают максимумы, а в других – минимумы интенсивности света; при этом происходит перераспределение световой энергии в пространстве.
Когерентные волны – это волны с одинаковой частотой v, с постоянной в течение
длительноговремениразностьюфаз =(f 2 −f 1) ираспространяющиесяводнойплоскости.
Амплитуда результирующего колебания в какой-либо точке пространства:
|
|
|
|
I = I1 + I2 + 2I1I2cos d: (4.2) - если колебания синфазные f 1 =f 2 (отличаются на четное число p), то Imax = 4I;
-если колебания протекают в противофазе f 1 −f 2 (отличаются на p), то Imin = 0. Оптической разностью хода двух волн называется разность оптических длин путей,
проходимых волнами:
|
Оптической длиной пути световой волны называется произведение геометрической длины пути, пройденного светом в среде, на показатель преломления этой среды:
L = n·S. (4.4) Оптической разности хода ∆ соответствует изменение разности фаз волн
|
|
где 0=n ×l – длина волны света в вакууме, l – длина волны в среде с показателем преломления n.
Условие максимумов интенсивности света при интерференции:
∆ = ± 2m2, d = 2 p m,
где m=0, 1, 2, ¼ порядок интерференции – число l, укладывающихся разностьхода ∆.
Условие минимумов интенсивности света при интерференции: ∆ = ± (2m + 1) l,
d=(2m + 1)p.
(4.6)
(4.7) на оптическую
(4.8)
(4.9)
В опыте Юнга оптическая разность хода для произвольной точки интерференционной картины на экране:
|
где L – расстояние от экрана до источников, d – расстояние между когерентными источниками (d << L).
Положениекоордината m – го максимума на экране определяется выражением:
|
положение координата m – го минимума на экране:
|
|
xmin = d, (4.12)Расстояние между двумя соседними максимумами или минимумами m и (m+1) порядка,
|
|
|
пластинах (полосы равного наклона) и на пластинах переменной толщины (полосы равной толщины).
Интерференционные полосы, возникающие в результате наложения лучей, падающих на плоскопараллельную пластину под одинаковыми углами, называются полосами равного наклона.
Интерференционные полосы возникающие при отражении от мест пластинки, имеющих одинаковую толщину, называются полосами равной толщины.
Оптическая разность хода световых волн, отраженных от верхней и нижней поверхностей тонкой плоскопараллельной пластинки или пленки (полосы равного наклона), находящейся в воздухе:
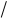∆ = 2dn2 − sin2i +l 2, (4.14)
где d – толщина пластинки (пленки), n – показатель преломления вещества пластинки, i – угол падения лучей.
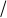Формула (4.14) выведена для случая, когда по обе стороны от пластинки находится одинаковая среда. Второе слагаемое в (4.14) учитывает изменение оптической длины пути световойволнынаl 2 приотраженииееотоптическиболееплотнойсреды(диэлектрика),вследствие того, что фазы колебаний волны меняется на величину p.
В проходящем свете отражение световой волны происходит от среды, оптически менее плотной, и дополнительной разности хода световых лучей не возникает.
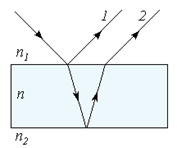Если тонкая пластинка окружена различными средами, то в зависимости от соотношения между показателями преломления сред n1, n2 и пластинки n возможны следующие случаи (рис. 15):
а)если n>n1, n>n2, то только луч 1, отраженный от границыс оптически более плотной средой, «теряет» l 2;
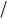
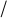б) если n<n1, n<n2 – «теряет» l 2 только луч 2; в)если n1 < n<n2 – оба луча «теряют» l 2;
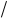г)если n1 > n>n2 –ни один луч не «теряет» l 2. Рис.15
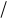Для случаев а и б соотношение (4.14) остается в силе. Для случаев в и г в формуле (4.14) величину l 2 надо отбросить, т.к. «потеря» 2 обоими лучами не скажется на их
разности хода.
|
Оптическая разность хода световых волн, поверхностей клина переменной толщины или находящегося в воздухе:
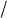∆ = 2d × n × cos g +l 2,
отраженных от верхней пленки (полосы равной
и нижней толщины),
(4.15)
где d – толщина клина (пленки) в данной точке, n – показатель преломления клина, – угол
преломления лучей в клине.
Полосы равной толщины, имеющие форму концентрических колец и называемые кольцами Ньютона, наблюдаются при интерференции света в тонком зазоре с n между плоской стеклянной пластинкой и плотно прижатой к ней плосковыпуклой линзой.
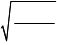
Радиусы светлых колец Ньютона в отраженном свете (или темных в проходящем):
|
|
|
|
mR
n
m = 0,1,2 …, (4.17)
где m – порядковый номер кольца, R – радиус кривизны поверхности линзы, соприкасающейся с плоскопараллельной стеклянной пластинкой, l – длина световой волны в среде между линзой и пластинкой.
Формулы (4.16), (4.17) выведены в предположении, что пластинка и линза имеют одинаковые показатели преломления.
Решение тестовых задач раздела «Интерференция света»
Тест 1
Складываются два гармонических колебания одного направления с одинаковыми периодами. Результирующее колебание имеет минимальную амплитуду при разности фаз, равной …
А) Б) 0 В) 4 Г) 2 Решение:
|
d=(f 2 −f 1)=p.
Ответ: А.
Тест 2
При каком соотношении между периодами колебаний и разностью фаз колебаний двух волн возможно явление интерференции …
|
|
|
|
Решение:
Явление интерференции наблюдается, если происходит наложение двух когерентных
|
Ответ: Г.
|
Тест 3
Две интерферирующих волны оптическойразностихода, равной ∆
А) 4 Б) 2
максимально усилены, если число 2 l, составляет …
В) 1
полуволн на их
Г) 1/2
Решение:
равно 4. Ответ: А.
Тест 4
Оптическая разность хода двух интерферирующих лучей монохроматического света равнаl /2 (l – длина волны). При этом разность фаз колебаний равна…
А) 2
Решение:
Для определения
Б) 4
разности фаз колебаний
В) 2
воспользуемся
Г)
формулой (4.5): d = 2 ∆,
|
Ответ: Г.
Тест 5
Складываются два гармонических колебания c одинаковыми направлениями и периодами с амплитудами 3 см и 4 см. При разности фаз /2 результирующее колебание имеет амплитуду (в см), равную …
А) 1 Б) 5 В) 7 Г) 25
Решение:
|
выражением(4.1): А =
Выполним расчет: А =
А2 + А2 + 2ААcos.
32 + 42 + 2 × 3 × 4 × cos p = 5 см.
Тест 6
Складываются два гармонических частотами и равными амплитудами
результирующего колебания равна …
|
одного направления с одинаковыми разности фаз d =p /2 амплитуда
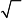
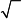
Решение:
Амплитуда результирующего колебания в какой-либо точке пространства определяется
|
|
|
|
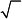
Ответ: А.
| |||||
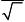
Тест 7
результирующего колебания равна …
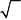
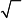
Решение:
Амплитуда результирующего колебания в какой-либо точке пространства определяется
|
|
|
|
Тест 8
|
|
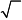
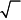
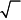
Решение:
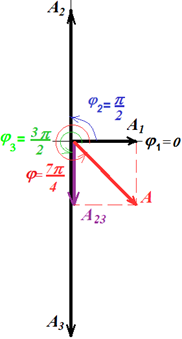
Определим амплитуду и фазу результирующего колебания графическим способом. Построим векторную диаграмму (рис. 16), на которой отложим в масштабе амплитуды колебаний: А1, А2, А3 и начальные фазы колебаний: j1=0, j2=p/2, j3=3p/2.
|
Рис. 16
Сложим вектора с
|
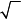Выполнимрасчет амплитуды: A =(3 − 2) 2 + 12 = 2 см.
|
|
|
|
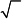
2 = 4. Тогда f = 3 + 4 = 4.
Ответ: А.
Тест 9
В опыте Юнга (рис. 17) расстояние между щелями d=0,5 мм. Расстояние от щелей до экрана L = 2 м. Расстояние от центра экрана до точки М равно х = 2 мм. Оптическая разность хода волн от источников S1 и S2 до точки М (в м) равна …
А) 8 Б) 0, 5 В) 7, 5 × 10 − 7 Г) 2, 5 × 10 − 7 Д) 5 × 10 − 7
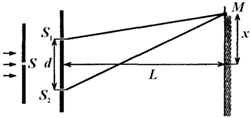Рис. 17
Решение:
|
Ответ: Д.
Date: 2015-05-09; view: 3037; Нарушение авторских прав