Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Система связей между термодинамическими функциями. Уравнения Гиббса - Гельмгольца. Соотношения Максвелла
|
|
 |  | ||
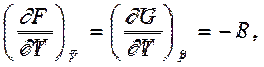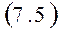Термодинамическое тождество (5.4) TdS = dU + PdV и определения термодинамических потенциалов H = U + PV (6.3), F = U – TS (6.5) и (6.7) G = U – TS+ PV позволяют записать полные дифференциалы энтальпии, свободной энергии и потенциала Гиббса в виде: dH = TdS + VdP, dF = - SdT – PdV, dG = - SdT + VdP. Отсюда сразу следуют связи
 |
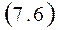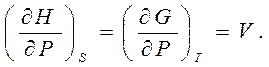(7.7)
 |  | ||
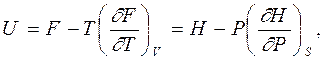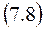Если подставить выражения для энтропии из (7.6) в уравнения (6.5) и (6.7) и учесть (6.3), то получатся уравнения Гиббса-Гельмгольца, связывающие термодинамические потенциалы друг с другом и с их производными по термодинамическим параметрам
 |  | ||
 |  | ||
 |  |
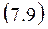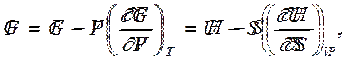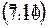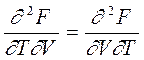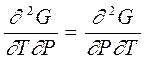Из выражений для полных дифференциалов свободной энергии и потенциала Гиббса (dF = - SdT – PdV и dG = -SdT + VdP) и по свойству равенства перекрестных производных
 | |||||
 |  | ||||
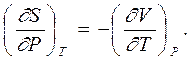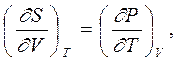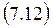получаем соотношения Максвелла
Слева в этих уравнениях стоят скорости изменения энтропии в изотермических процессах при изменении объема или давления, а правые части этих уравнений легко находят опытным путем.
 |
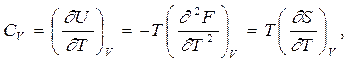Вторые производные от потенциалов связывают важные для практики значения теплоемкостей при постоянном объеме или давлении с изменением энтропии
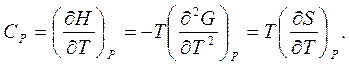(7.13)
Оба эти уравнения (7.13) имеют отношение к третьему началу термодинамики (теореме Нернста): При приближении температуры к абсолютному нулю энтропия однородной системы стремится к нулю, LimS]T=0 = 0. Строго говоря, энтропия обязана стремиться к постоянному значению, которое Макс Планк предложил для определённости всегда считать равным нулю.
В рамках феноменологической термодинамики третье начало термодинамики фиксирует точку отсчета энтропии. Энтропия при этом может быть вычислена по формуле
 |  | ||
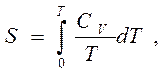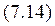из которой видно, что вблизи абсолютного нуля теплоемкость должна становиться бесконечно малой (чтобы интеграл не обращался в бесконечность). Значит, никакими способами нельзя отнять теплоту у термодинамической системы, и абсолютный нуль недостижим.
 |
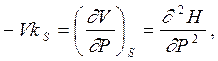Вторые производные от термодинамических потенциалов связаны также с коэффициентами сжимаемости - изотермическим kT и адиабатным kS - при соответствующих процессах (или с обратными им величинами – модулями всестороннего изотермического ВТ и адиабатного ВS сжатия). Произведения этих коэффициентов на объем дают вторые производные по давлению от термодинамического потенциала Гиббса G и энтальпии Н
 |  | ||
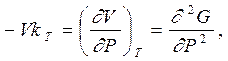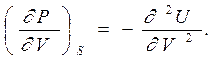а обратные им величины дают вторые производные по объему от
 |
свободной энергии F и от внутренней энергии U
 |
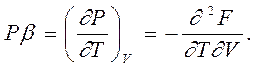Для изохорного термического коэффициента давления b его произведение на давление (Рb) дает перекрестную производную от свободной энергии по температуре и объему со знаком минус (сравните с уравнениями 7.12), так как в первом уравнении справа от знака равенства стоит произведение давления Р на изохорный коэффициент температурного давления β, а в правом уравнении – произведение объема V на изобарный коэффициент теплового расширения α со знаком минус
Вся эта система связей между термодинамическими функциями позволяет, зная любой из термодинамических потенциалов, найти все остальные. На практике снимают доступные экспериментальным измерениям зависимости и по ним строят графики или составляют таблицы зависимостей термодинамических потенциалов и энтропии от термодинамических параметров для самых различных веществ, а потом подбирают наиболее подходящие вещества в качестве самых эффективных рабочих тел в термодинамических процессах. Но это уже чисто технические задачи.
8. РЕАЛЬНЫЕ ТЕРМОДИНАМИЧЕСКИЕ СИСТЕМЫ
И ФАЗОВЫЕ ПРЕВРАЩЕНИЯ
Date: 2015-05-09; view: 1058; Нарушение авторских прав