
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Модель газа Ван-дер-Ваальса. Изотермы Ван-дер-Ваальса
|
|
Модель идеального газа сыграла важную роль в исследованиях тепловых процессов. Она позволила выявить существование и зависимость от температур нагревателя и холодильника максимального КПД тепловых машин, позволила построить термодинамическую шкалу температур и, наконец, позволила понять второе начало термодинамики и ввести меру хаотичности состояния термодинамической системы – энтропию. Кроме всего этого, в силу предельной простоты термического уравнения состояния идеального газа, использование этого уравнения позволило найти фундаментальные, то есть обладающие всеобщностью, универсальностью, связи между термодинамическими потенциалами, термодинамическими параметрами и энтропией. Эти связи позволяют находить практически полезные характеристики термодинамических объектов даже в тех случаях, когда мы ничего не знаем об их термических уравнениях состояния (и даже вне зависимости от их агрегатных состояний, хотя сам идеальный газ имеет только одно агрегатное состояние – газообразное). Таким образом, идеальный газ оказался способным моделировать тепловое поведение в термодинамических процессах не только газообразных, но и жидких и твердых тел.
Однако целый ряд свойств реальных природных тел и процессов модель идеального газа заведомо не в состоянии объяснить в силу исключения из этой модели некоторых характеристик микрообъектов, составляющих термодинамическую систему. Так, например, модель идеального газа не может объяснить переход вещества из газообразного состояния в жидкое, поскольку за это ответственны силы взаимодействия между молекулами на расстоянии, которыми в этой модели пренебрегают. Эти силы получили название сил Ван-дер-Ваальса, но мы не будем подробно останавливаться на их природе, отметив только сам факт их существования.
Напомним, что в модели идеального газа пренебрегают размерами молекул, считая их материальными точками, а также их взаимным притяжением, которым действительно можно пренебречь, когда средние расстояния между молекулами измеряются десятками их радиусов и более. В этих случаях кинетическая энергия молекул газа много больше их потенциальной энергии взаимодействия на расстоянии, и этой потенциальной энергией можно пренебречь. Таким образом, модель идеального газа (как и любая модель) имеет свои границы применимости.
Если рассматривать явления природы, в которых собственные размеры молекул и их взаимодействие на расстоянии играют существенную роль (как, например, при фазовом переходе вещества из газообразного состояния в жидкое), то, естественно, такие явления не могут быть описаны с помощью уравнения состояния идеального газа. Следовательно, необходимо использовать другие модели, больше отвечающие реальности. Законы взаимодействия между молекулами можно постараться учесть, однако при этом все время надо помнить, что эти законы отличаются у разных веществ, и, следовательно, учитывающая их модель не будет обладать такой универсальностью как модель идеального газа.
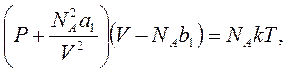 |
Следующей по простоте моделью (после модели идеального газа) является модель газа, предложенная голландским физиком Ван-дер-Ваальсом. В ней учитывается как наличие собственного объема молекул, так и добавочное давление в газе, вызванное взаимным притяжением молекул. Отдельные молекулы, находящиеся в приграничном слое вещества, испытывают направленное внутрь силовое действие, которое можно считать пропорциональным концентрации молекул, а число молекул также пропорционально концентрации, и, следовательно, добавочное давление пропорционально квадрату концентрации (N/V)2 молекул газа. А если еще из номинального объема газа вычесть собственный объем молекул, чтобы учитывать только свободный для движения молекул объем, то вместо уравнения идеального газа получается уравнение состояния для газа Ван-дер-Ваальса,
где a1 и b1 - две подгоночные константы, отнесенные к одной молекуле. В расчёте на один моль эти постоянные Ван-дер-Ваальса (не универсальные, а разные у разных веществ) суть а = NA2a1 и b = NAb1.
Теперь уравнение Ван-дер-Ваальса (в расчете на один моль) принимает вид
(P + a/V2)(V – b) = RT. (8.1)
Это уравнение качественно правильно отражает поведение реальных газов, хотя в количественном отношении полного совпадения нет.
Молярные постоянные Ван-дер-Ваальса а и b для всех веществ измерены и занесены в соответствующие таблицы.











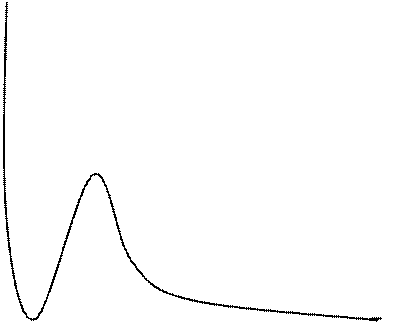
 Если нарисовать изотермы газа Ван-дер-Ваальса в координатах давление-объем, то они имеют вид, представленный на Рис. 4.
Если нарисовать изотермы газа Ван-дер-Ваальса в координатах давление-объем, то они имеют вид, представленный на Рис. 4.

 Р
Р

 |
РК К

 Пар
Пар
С
ТК



Д

 в
в
 VА VК VД V
VА VК VД V
Рис. 4. Изотермы газа Ван-дер-Ваальса
Как видно из рис.4, ниже некоторой (критической) температуры Тк изотермы дают S-образный участок кривой АВСД, который в опытах с реальными газами не наблюдается. Вместо него между точками А и Д сосуществуют две фазы – жидкая и газообразная. Здесь газ частично конденсируется в жидкость так, что при изменении объема давление все время остается постоянным между точками А и Д, изменяется лишь доля молекул газа, находящегося в состоянии насыщенного пара, а изотерма представляет собой горизонтальную прямую. При температурах, заметно превышающих критическую температуру, изотермы Ван-дер-Ваальса не отличаются существенно от гиперболических изотерм идеального газа (Рис.1).
Точка К на критической изотерме представляет собой точку перегиба кривой. Как известно из математики, в точке перегиба не только первая, но и вторая производная обращается в нуль. Это позволяет в данной точке связать с постоянными Ван-дер-Ваальса значения давления Рк, объема Vк и температуры Тк, которые получили название критических. Они определяются из уравнений
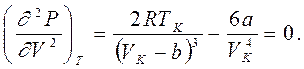 |
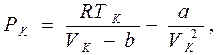
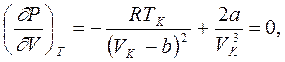 |
Сравнивая второе и третье уравнения, получаем
VK = 3b, (8.2) а подстановка VK во второе уравнение дает
ТК = 8а/27Rb, (8.3)
и подстановка VK и ТК в первое уравнение дает
PK = a/27b2. (8.4)
Знание координат критической точки (VK, PK, ТК), найденное опытным путем, позволяет выразить через них газовую постоянную R и обе константы Ван-дер-Ваальса по формулам
R = 8PKVK/3ТК, b = VK/3, a = 3PKVK2 (8.5)
Date: 2015-05-09; view: 1413; Нарушение авторских прав