
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Энтропия как мера хаотичности состояния термодинамической системы. Формула Клаузиуса для вычисления изменения энтропии в обратимом процессе. Термодинамическое тождество
|
|
Новое свойство требует введения нового понятия, позволяющего качественно и количественно охарактеризовать это свойство, и, естественно, новой терминологии. Клаузиус назвал (1865) величину, измеряющую степень хаотичности состояния термодинамической системы, энтропией.
Что должна представлять собой эта величина и функцией чего она должна являться? Как измерить молекулярный беспорядок (хаос)? Как энтропия выражает степень хаотичности состояния термодинамической системы?
Обратимся опять к модели идеального газа, чтобы понять, в чем проявляется и при каких изменениях параметров изменяется согласованность (корреляция) в состояниях отдельных частиц термодинамической системы.
В механической теории теплоты (которая считает справедливыми в микромире законы классической механики) состояние термодинамической системы полностью определяется координатами и импульсами всех частиц, образующих термодинамическую систему, а хаотичность состояния системы проявляется в существовании дисперсии (квадрата среднеквадратичного отклонения от среднего значения) микропараметров, определяющих состояние термодинамической системы. Дисперсия является мерой рассеяния случайных величин, а корень квадратный из дисперсии (стандарт случайной величины) дает среднеквадратичное отклонение случайной величины от ее среднего значения. При хаотическом движении микрочастиц их координаты и импульсы рассматриваются как случайные величины. Следовательно, изменение степени хаотичности состояния должно сопровождаться изменением дисперсии этих параметров (и соответственно, их стандарта – корня квадратного из дисперсии).
Модель идеального газа позволяет понять, о чем идет речь. Здесь частицы, участвующие в тепловом движении, хотя и двигаются вполне хаотически, проявляют, тем не менее, некоторую корреляцию (соответствие) своих состояний, так как существует некоторая согласованность в их движениях (импульсах) и некоторая упорядоченность расположения в пространстве (координатах). При термодинамическом равновесии сохраняется средний разброс импульсов около их среднего значения и разброс около среднего положения в пространстве (определяемый размерами сосуда с газом). Исторически сложилось так, что в термодинамике начали искать функцию, измеряющую не согласованность (корреляцию) состояний микрочастиц, а противоположную по смыслу функцию, измеряющую несогласованность микросостояний. Если под хаотичностью состояния понимать некоррелированность (несогласованность) состояний отдельных частиц термодинамической системы, то можно ввести величину, являющуюся мерой этой хаотичности и позволяющую количественно оценивать степень несогласованности состояний отдельных частиц системы, то есть степень хаотичности состояния системы (или, по крайней мере, ее изменение при изменении состояния системы). Разумеется, способы вычисления этой величины должны быть разными в феноменологической термодинамике и в статистической механике. Так в статистической механике эта функция состояния системы (мера статистически усредненного отклонения отдельных частиц системы от их усредненных положений в фазовом пространстве) вычисляется методами теории вероятностей.
Из рассмотренного примера с идеальным газом видно, что, поскольку хаотичность состояния термодинамической системы определяется независимым образом, как дисперсией координат, так и дисперсией импульсов частиц, то возможны такие изменения состояния системы, при которых величина, характеризующая степень хаотичности состояния системы, остается неизменной. Поскольку ее возрастание, например, за счет увеличения объема (увеличение дисперсии координат), может компенсироваться убыванием за счет уменьшения дисперсии импульсов при понижении температуры. Таково адиабатное расширение и сжатие газа (см. ПРИЛОЖЕНИЕ 3).
Если абсолютизировать модель идеального газа, то она позволяет также предсказать (по крайней мере, качественно) поведение искомой величины при изменении температуры. В силу самой модели идеального газа, очевидно, что его молекулы при абсолютном нуле температуры должны иметь неизменные, фиксированные координаты («упасть на дно сосуда» при внешнем силовом поле) и одинаковые, равные нулю импульсы. Это соответствует минимально возможным дисперсиям координат и импульсов и, значит, минимальному значению искомой функции. При повышении температуры дисперсия координат молекул идеального газа будет определяться только размерами сосуда (вне зависимости от температуры), а что касается дисперсии импульсов, то в рамках феноменологической термодинамики достаточно качественного указания на ее увеличение с ростом температуры (что очевидно, если мысленно повышать температуру системы, начиная с абсолютного нуля). Возможность точных количественных расчетов должны дать методы статистической механики.
При изучении новых явлений большую роль всегда играло знание величин, сохраняющихся в процессах, происходящих в изолированных системах. Огромное значение для развития механики и электричества имело открытие законов сохранения энергии, импульса и момента импульса. Поэтому естественно, что усилия исследователей тепловых закономерностей были направлены на обнаружение величин, сохраняющихся в термодинамических процессах, хотя качественное отличие термодинамики от механики очевидно: Процессы, в которых присутствует самопроизвольное выравнивание термодинамических параметров, обладают свойством необратимости, в то время как все чисто механические (без участия сил трения) процессы полностью обратимы.
Поскольку в термодинамике, наряду с необратимыми процессами, в принципе возможны также и обратимые процессы, то поиск функции, позволяющей измерить степень хаотичности состояния термодинамической системы, естественно начать с рассмотрения полностью обратимых процессов в изолированных системах. В силу полной обратимости процессов и замкнутости систем степень хаотичности состояния таких систем не должна изменяться, и, следовательно, надо искать функцию, сохраняющуюся в замкнутых системах при всех обратимых тепловых процессах (в том числе при преобразованиях теплоты в работу). Это означает, что изменение этой функции у любого из тел, включенных в замкнутую систему, должно компенсироваться равным по величине, но противоположным по знаку суммарным изменением этой функции у других тел этой изолированной системы.
По своему смыслу искомая функция должна быть функцией состояния системы. В противном случае, проводя циклически (в нужном направлении цикла) термодинамическую систему в начальное состояние с другим, меньшим значением этой функции, можно было бы, многократно повторяя цикл, свести к нулю хаотичность состояния, что противоречит невозможности всю теплоту преобразовать в работу. Следовательно, в циклических процессах, при возвращении термодинамической системы в первоначальное состояние (вне зависимости от пути возвращения и даже без требования замкнутости системы и обратимости процессов) полное изменение этой функции должно быть равно нулю.
Поиск функции состояния термодинамической системы, сохраняющейся в обратимых процессах в замкнутых (полностью изолированных от любых внешних воздействий) термодинамических системах, привел немецкого физика Рудольфа Клаузиуса к величине, первоначально получившей название «приведенная теплота». Понять, что это такое, можно из рассмотрения рабочего цикла все той же идеальной тепловой машины Карно.
Обратим внимание, что все сохраняющиеся величины носят экстенсивный характер, но сразу отметим, что ранее рассмотренная экстенсивная величина, характеризующая тепловые процессы, то есть теплота, передаваемая рабочему телу в цикле Карно, явным образом не сохраняется, несмотря на обратимость всех этапов цикла.
У нас уже есть соотношение (4.4): Q1/Q2 = T1/T2, утверждающее равенство отношения теплоты, полученной от нагревателя, к теплоте, отданной холодильнику, отношению температур нагревателя и холодильника. Уравнение можно переписать в виде отношения
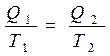
или, учитывая различия знаков для теплоты, получаемой или отдаваемой рабочим телом, Q1/T1 = - Q2/T2 , что может быть записано как Q1/T1 + Q2/T2 = 0.
Отношение переданной телу теплоты к его температуре получило первоначально название приведенной теплоты.
Уравнение
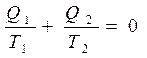
означает сохранение приведенной теплоты в цикле Карно.
Дифференциальная форма (для предельно малого цикла Карно) дает соответственно
δQ1/T1 + δQ2/T2 = 0.
Таким образом, рассмотрение цикла Карно показало, что в циклическом процессе сохраняется сумма «приведенных теплот».
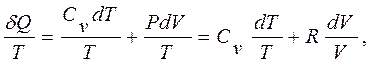 |
Кроме того, поскольку искомая функция должна быть функцией состояния и принимать прежнее значение при завершении цикла, то ее малое изменение должно быть полным дифференциалом (математическое требование, чтобы интеграл от такого дифференциала по замкнутому пути давал нуль). Малое количество теплоты dQ полным дифференциалом не является, так как зависит от вида процесса, в котором совершается передача теплоты. Для получения из dQ полного дифференциала следует воспользоваться известной в математике процедурой нахождения интегрирующего множителя. Сохранение приведенной теплоты подсказывает, что таким множителем может быть обратная абсолютная температура. Первое начало термодинамики (2.2) dQ = dU + dA для газа в форме dQ = CvdT + РdV и уравнение состояния идеального газа РV = RT позволяют убедиться, что это действительно так, что dQ/Т является полным дифференциалом, так как очевидно,
что справа стоит полный дифференциал функции двух переменных.
Гениальность Клаузиуса проявилась в том, что он увидел связь между изменением искомой функции состояния (изменением энтропии S) и поступлением в термодинамическую систему теплоты (то есть энергии, передаваемой через хаотическое движение микрочастиц). По Клаузиусу, это изменение определяется дифференциальным соотношением
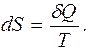 (5.1)
(5.1)
Здесь принципиально важна обратимость процесса передачи теплоты.
Из этого соотношения сразу следует, что в обратимых процессах без теплообмена с внешними телами энтропия сохраняется (система не обязательно изолирована и может обмениваться энергией с окружением, но через работу). Так, например, обратимое адиабатное расширение или сжатие газа изоэнтропно, и степень хаотичности состояния системы сохраняется.
Возможность (по крайней мере, теоретическая) переводить систему из одного состояния в другое состояние обратимым способом через передачу теплоты (например, в квазистатическом процессе) имеет принципиальное значение, так как позволяет вычислять разность значений энтропии между двумя любыми состояниями термодинамической системы посредством интегрирования дифференциала поступающей в систему приведенной теплоты (дифференциала энтропии) по формуле
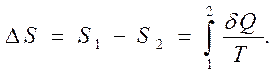 | 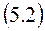 | ||
Этот прием вычисления изменения энтропии обладает всеобщностью, универсальностью, так как не связан с реально осуществляемым путем перехода системы из одного равновесного состояния в другое. Это так потому, что хотя разность энтропий находится через вычисления, относящиеся к обратимому, идеализированному переходу, но сама система может переходить из одного равновесного (начального) в другое равновесное (конечное) состояние любым (в том числе самопроизвольным и, следовательно, необратимым) способом.
Возможность написать в обобщенном законе сохранения энергии (2.2) теплоту dQ через дифференциал энтропии как TdS позволяет представить первое начало термодинамики выражением
ТdS = dU + dA, (5.3)
получившим название термодинамическое тождество, которое записывается для газообразных тел в виде
TdS = СVdT + PdV. (5.4)
Date: 2015-05-09; view: 1168; Нарушение авторских прав