
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Идеального газа. Работу идеального газа в изотермическом процессе
|
|
 | 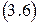 | ||
Работу идеального газа в изотермическом процессе, представленную площадью фигуры (Рис.1), лежащей под изотермой и ограниченной ординатами начала и конца процесса, легко вычислить, учитывая уравнение (3.1) и взяв интеграл в пределах от V1 до V2
Изотермическими можно с хорошей степенью приближения считать достаточно медленные термодинамические процессы при отсутствии теплоизоляции, когда температуры всех тел успевают выровняться (время температурной релаксации много меньше времени, характерного для рассматриваемого процесса), и температуру всюду можно считать одинаковой.
Большой интерес для практики представляют также адиабатные процессы, которые протекают без теплообмена термодинамической системы с окружающей средой. Таковыми можно считать все процессы, протекающие либо в условиях хорошей теплоизоляции, либо настолько быстро, что теплообмен не успевает произойти (время релаксации много больше характерного времени процесса). Такие процессы можно с хорошим приближением считать обратимыми. В этом случае 1-е начало термодинамики (2.7) для газа записывается в виде
dQ = CvdT + PdV = 0. (3.7)
Воспользовавшись уравнением состояния идеального газа (3.1), уравнение (3.7) можно переписать в виде
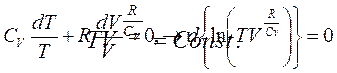 |
или
Воспользовавшись уравнением (2.8), получаем
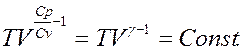 | 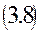 | ||
Здесь использовано общепринятое обозначение отношения теплоемкости при постоянном давлении к теплоемкости при постоянном объеме символом g, то есть g = Cp/ Cv.
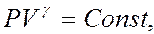 |
Поскольку уравнение состояния (3.1) связывает три термодинамических параметра, оставляя независимыми лишь два из них, то уравнение адиабаты (3.8) можно переписать через другие параметры, например, через давление и объем, то есть в координатах (P,V)
(3.9)
или в координатах температура-давление (T,P)
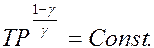 | 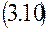 | ||
Очевидно, что все три выражения (3.8), (3.9) и (3.10) равносильны.
Отметим, что теоретическое значение отношения теплоемкостей при постоянном давлении и постоянном объеме g может быть вычислено на основе модели структуры молекул идеального газа и гипотезы о равнораспределении кинетической энергии теплового движения по степеням свободы газа (см. ПРИЛОЖЕНИЕ 2). Впрочем, это относится уже к статистической механике, а экспериментальное значение g может быть найдено, например, по скорости распространения звука в газе.
Измерить показатель адиабаты по скорости распространения звука в газе можно, воспользовавшись аналогией с распространением звука в твердых телах, где скорость звука, как известно, выражается через модуль Юнга Е и плотность вещества r формулой v2 = E/r. Теперь выражение для скорости звука в газе можно написать в виде
v2 = B/r,
где В - модуль всестороннего сжатия в адиабатном процессе, то есть величина, обратная коэффициенту адиабатной сжимаемости (см. в параграфе 1.2. аналогичную величину для изотермического процесса BT =1/kT). Следовательно,
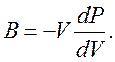 |
Выражение для В в правой части уравнения v2 = B/r легко найти, дифференцируя уравнение адиабаты (3.9), откуда имеем
dP∙Vg + gPVg-1dV = 0.
И, следовательно,
В = gP.
Окончательно получаем, что скорость звука в газе (в случае применимости модели идеального газа, когда можно считать, что P/r = RT/M) связана с показателем адиабаты формулой
v2 = gRT/M.
По этой формуле из экспериментальных данных о скорости звука можно определить показатель адиабаты.
Из этой зависимости следует также, что скорость звука в газах растет с увеличением температуры, что также поддается экспериментальной проверке.
4. ОСОБЕННОСТИ ПРЕОБРАЗОВАНИЯ ТЕПЛОТЫ В РАБОТУ
4.1. Тепловые машины и термодинамические циклы
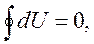 |
Первое начало термодинамики как закон сохранения энергии, обобщенный на участие тепловых процессов, не накладывает никаких ограничений не только на превращение работы в теплоту, но и на обратное превращение теплоты в работу. Из математической формы записи первого начала (2.2): dQ = dU + dA сразу видно, что при выполнении тепловой машиной замкнутого термодинамического процесса (цикла), то есть при возвращении рабочего тела машины в исходное состояние, когда изменение его внутренней энергии как функции состояния равно нулю,
как будто бы существует принципиальная возможность преобразования всей полученной рабочим телом за цикл теплоты в работу, поскольку интегрирование по любому циклическому процессу дает Q = A
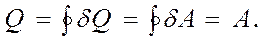 |
Напомним, что работа является мерой энергии, переданной силовым, механическим способом, а теплота (тепло или количество тепла) – мерой энергии, переданной тепловым, немеханическим способом. Говоря о теплоте, мы всегда должны помнить, что речь идет не о «форме энергии», а о форме передачи энергии посредством микроскопического неупорядоченного движения микрочастиц, в отличие от их макроскопически-упорядоченного движения (при движении системы частиц как целого), характерного для механической формы передачи энергии, когда мы употребляем термин работа.
Заметим, что, с одной стороны, практика постоянно демонстрирует нам ничем не ограниченную возможность преобразования работы в теплоту ( как принято для краткости называть преобразование энергии движения макроскопических тел в энергию хаотического движения микрочастиц). Всю работу можно превратить в теплоту. Примером может служить нагревание тел при трении.
С другой стороны, при существовании принципиальной возможности преобразования теплоты в работу (тепловые машины существуют) практика постоянно указывает на существование некоторого ограничения относительно этого преобразования. Весь опыт работы тепловых машин показывает невозможность осуществления рабочим телом машины циклического процесса без участия двух тепловых резервуаров различной температуры и без передачи части полученной у более горячего резервуара теплоты резервуару более холодному. Возможность преобразования взятой у нагревателя теплоты в работу оказывается лишь частичной.
Практический интерес представляют в основном тепловые машины, циклически работающие как источники механической энергии, не зависящие от таких случайных факторов, как месторасположение природных водных потоков или капризов погоды, с чем связано использование водяных и ветровых силовых установок. Важность циклических процессов в том, что хотя изменение состояния термодинамической системы в цикле равно нулю, но количество полученной от нагревателя теплоты и количество совершенной системой работы может не равняться нулю. То есть цикл позволяет систематически преобразовывать передачу энергии тепловым способом в передачу энергии силовым способом, или, как говорят для краткости, преобразовывать теплоту в работу.
Итак, практика человечества упорно показывает, что всю теплоту, взятую из некоторого теплового резервуара (именуемого обычно нагревателем) ни в каком циклическом процессе не удается превратить в работу. Часть теплоты приходится отдавать охладителю - «холодильнику», без теплового контакта рабочего тела с которым, невозможно осуществить циклический процесс так, чтобы иметь избыток полученной работы над работой, затраченной для возвращения рабочего тела в исходное состояние. Следовательно, для осуществления рабочего цикла тепловая машина должна иметь кроме рабочего тела и горячего резервуара, из которого берется теплота, еще один резервуар с более низкой температурой. Это холодильник, куда частично должна отводиться теплота, чтобы процесс возвращения в исходное состояние совершался при более низкой температуре и поэтому с меньшей затратой работы. При преобразовании теплоты в работу существует какое-то дополнение к закону сохранения энергии, не позволяющее просто брать теплоту от нагревателя и преобразовывать ее в работу.
Для прояснения этого вопроса необходимо рассмотреть принципиальную сторону работы тепловых машин.
Теория тепловых преобразований должна дать ответ на два основных вопроса практики:
1. Существует ли наивысший, предельный коэффициент полезного действия (КПД) для тепловых машин (меньший 100%)?
2. Если такой КПД существует, то чем определяется его величина, то есть, зависит ли КПД от вида вещества, используемого в качестве рабочего тела, или от типа используемых в тепловой машине процессов, или еще от чего-либо?
Французский инженер Сади Карно в опубликованной в 1824 году работе "Размышление о движущей силе огня" правильно ответил на оба эти вопроса. Ответы он получил, рассматривая идеализированный циклический процесс, получивший впоследствии название цикла Карно (иногда говорят о тепловой машине Карно).
Date: 2015-05-09; view: 977; Нарушение авторских прав