
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Вынуждающая сила 3 page
|
|
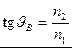 .
.
РИС.28-5
Угловая зависимость коэффициента отражения:
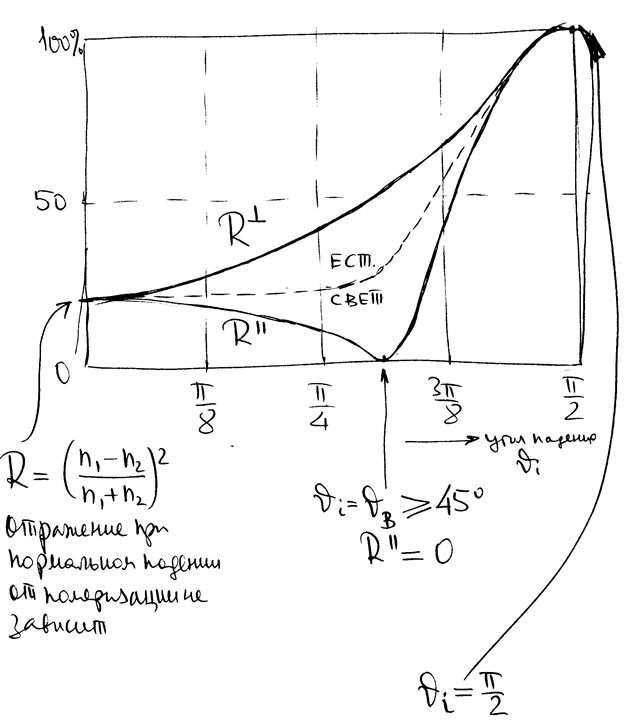
РИС.28-6
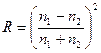 - отражение при нормальном падении от поляризации не зависит,
- отражение при нормальном падении от поляризации не зависит, 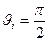 - при скользящем падении коэффициент отражения равен 100% и не зависит от поляризации.
- при скользящем падении коэффициент отражения равен 100% и не зависит от поляризации.
Мы вывели соотношения между амплитудами отраженных и преломленных волн в зависимости от свойств границы раздела и от угла падения света. При этом выяснилось, что для электромагнитных волн, поляризованных в плоскости падения, энергетический коэффициент отражения обращается в нуль при некотором характерном угле падения, называемом углом Брюстера: 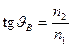 .
.
Это явление можно использовать для создания поляризованной электромагнитной волны.
РИС.28-7
Черное стекло, чтобы отражение от второй границы не искажало ситуацию.
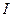 - интенсивность света, прошедшего анализатор.
- интенсивность света, прошедшего анализатор.
Степень поляризации: 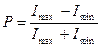 .
.
Для плоско (линейно) поляризованных электромагнитных волн 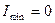 , то есть
, то есть  , тогда как для естественной (неполяризованной) волны
, тогда как для естественной (неполяризованной) волны 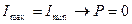 .
.
Поляризация при преломлении
Энергетический коэффициент прозрачности=
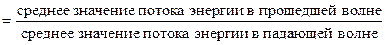 =
=
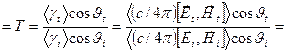
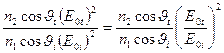 .
.
Подставляя в выражение для круглых скобок 2 формулу Френеля, находим:
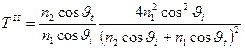 =
= 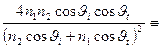
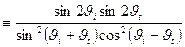 .
.
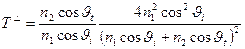 =
= 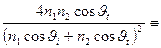
 .
.
Во-первых, можно убедиться в справедливости закона сохранения энергии:
 Доказывается простой подстановкой.
Доказывается простой подстановкой.
Во-вторых, можно убедиться в том, что свет, поляризованный в плоскости падения несколько лучше проходит через границу раздела, чем свет с перпендикулярной поляризацией. (Поскольку при падении под углом Брюстера 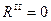 , то куда деваться электромагнитной волне с такой поляризацией, чтобы обеспечить закон сохранения энергии? Только проходить!)
, то куда деваться электромагнитной волне с такой поляризацией, чтобы обеспечить закон сохранения энергии? Только проходить!)
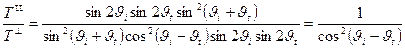 .
.
Из формулы видно, что во всех случаях, кроме нормального падения (когда 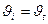 и
и 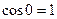 ,
, 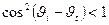 и
и 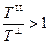 .
.
Прохождение через одну пластинку (две границы раздела)
Рассмотрим соотношение интенсивностей волн различной поляризации.
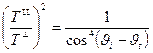 ;
;
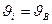 ,
,  ;
;
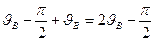 ,
,
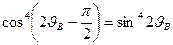 ,
, 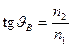 ,
,
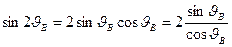 =
=
{с учетом 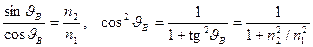 }
}
= 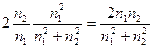 .
.
Если ввести относительный показатель преломления 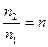 , то
, то
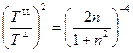 ;
; 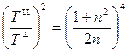 .
.
Реальные числа: «стекло-воздух», 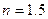 ;
;
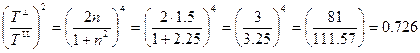 .
.
Приходится брать до десятка пластинок, чтобы получить эффективную поляризацию (большие потери на отражение!). Лучше, когда большой показатель преломления – например, «германий-воздух»: 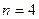 .
.
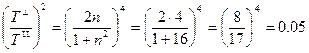 .
.
Интенсивность 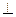 -поляризованной волны составляет 5% интенсивности
-поляризованной волны составляет 5% интенсивности  -поляризованной волны.
-поляризованной волны.
Фазовые соотношения между падающей и отраженной волнами
Определяются знаком тригонометрических функций в формулах Френеля.
1930 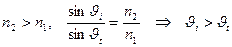 .
.
А 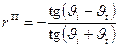 .
.
При нормальном падении (или при почти нормальном падении) 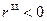 , то есть отражение происходит с изменением фазы на
, то есть отражение происходит с изменением фазы на 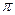 .
.
При увеличении угла падения – два частных случая:
а) 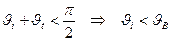 , отраженная и падающая волна противофазны;
, отраженная и падающая волна противофазны;
 |
б)
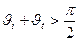 , числитель
, числитель 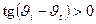 , знаменатель
, знаменатель 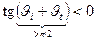 , отраженная и падающая волны синфазны.
, отраженная и падающая волны синфазны.
РИС.28-8
Б. 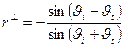 .
.
При переходе в оптически более плотную среду, 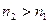 ,
, 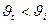 , числитель и знаменатель
, числитель и знаменатель 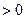 , поэтому разность фаз
, поэтому разность фаз 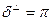 , отраженная и падающая волны противофазны.
, отраженная и падающая волны противофазны.

РИС.28-9
II. Переход из оптически более плотной среды в оптически менее плотную, 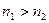 .
.
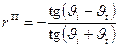 .
.
Пока  , отражение происходит без изменения фазы,
, отражение происходит без изменения фазы,
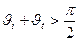 - волны противофазны.
- волны противофазны.
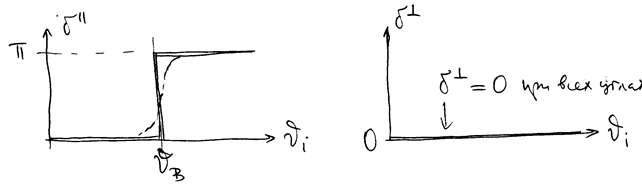
РИС.28-10
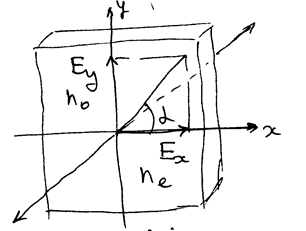
Сложение двух электромагнитных волн, поляризованных во взаимно перпендикулярных направлениях
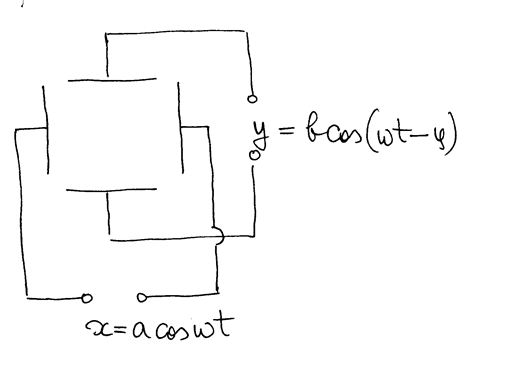 |
Рассмотрим результат сложения двух электромагнитных волн, поляризованных во взаимно перпендикулярных направлениях и имеющих разную амплитуду и фиксированный сдвиг фаз.
Какова будет траектория конца вектора, проекции которого меняются по такому закону?
РИС.28-11
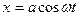 ,
,
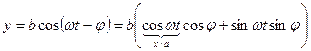 ,
,
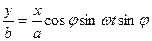 .
.
Отсюда:
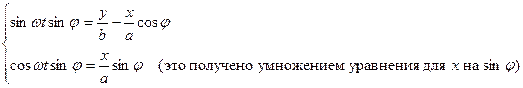 .
.
Возводим в квадрат и складываем:
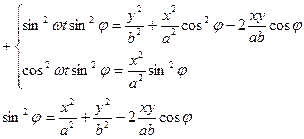
Последнее выражение и есть уравнение эллипса. Его форма и ориентация относительно осей 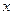 и
и 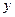 зависят от амплитуд
зависят от амплитуд 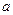 ,
, 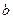 и разности фаз
и разности фаз 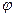 . Это все характеризует границу раздела.
. Это все характеризует границу раздела.
Рассмотрим несколько частных случаев, чтобы лучше представить себе, как возникает эллиптическая поляризация (дополнительный материал).
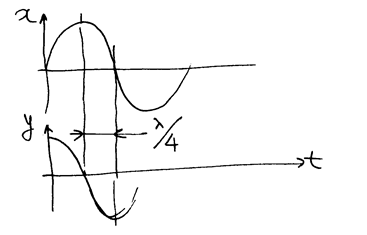 |
А.
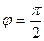 , или разность хода волн, поляризованных во взаимно перпендикулярных направлениях,
, или разность хода волн, поляризованных во взаимно перпендикулярных направлениях, 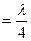 .
.
РИС.28-12
Подставляя в полученное выше уравнение 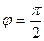 , находим:
, находим:
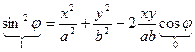 Þ
Þ 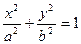 .
.
 |
Если
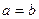 , то эллипс превращается в окружность (циркулярная поляризация).
, то эллипс превращается в окружность (циркулярная поляризация).
Реализация:
РИС.28-13
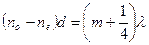
Если 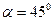 , то на пластинку падают две плоско поляризованные волны с одинаковыми амплитудами. На выходе из пластинки две волны – плоско поляризованные, а разность фаз задается оптической толщиной пластинки.
, то на пластинку падают две плоско поляризованные волны с одинаковыми амплитудами. На выходе из пластинки две волны – плоско поляризованные, а разность фаз задается оптической толщиной пластинки.
Б. Разность хода 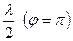 .
.
Эллипс вырождается в пару прямых 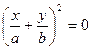 .
.
Полное внутреннее отражение
При переходе из оптически более плотной среды в оптически менее плотную среду 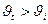 , так что при некотором
, так что при некотором 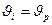
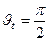 .
.
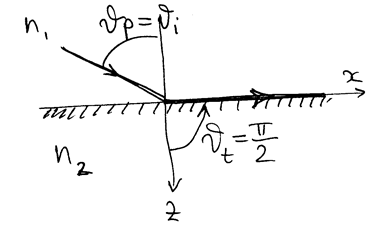 |
РИС.28-14
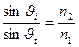 (
(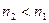 );
);
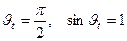 .
.
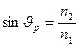 Þ
Þ  .
.
Вычислим электромагнитное поле во второй среде:
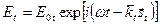 .
.
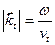 ,
, 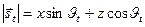 .
.
Подставляя эти выражения, имеем:
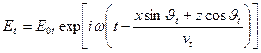 .
.
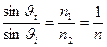 ,
, 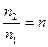 - относительный показатель преломления,
- относительный показатель преломления, 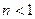 .
.
Так как 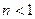 , то
, то 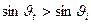 ,
,
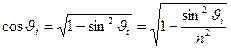 .
.
В случае полного внутреннего отражения:
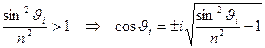 .
.
Получается преломленная волна в виде
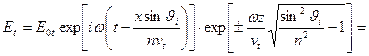
= 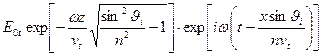 {в первой экспоненте стоит минус, потому что по направлению оси
{в первой экспоненте стоит минус, потому что по направлению оси 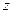 волна должна затухать; вторая экспонента – волна, бегущая по оси
волна должна затухать; вторая экспонента – волна, бегущая по оси 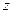 }.
}.
На какую глубину проникает волна во вторую среду?
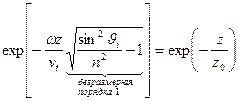 .
.
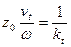 ~
~ 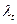 .
.
На глубине ~ 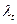 амплитуда прошедшей волны уменьшается втрое.
амплитуда прошедшей волны уменьшается втрое.
В условиях полного внутреннего отражения амплитуда прошедшей волны убывает в 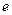 раз на глубине туннелирования.
раз на глубине туннелирования.
29 Классическая теория дисперсии
До сих пор мы рассматривали оптические (в широком смысле слова) явления, принимая как данное извне, свойства среды: диэлектрическую проницаемость 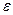 , магнитную проницаемость
, магнитную проницаемость 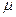 , показатель преломления
, показатель преломления 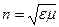 или комплексный показатель преломления
или комплексный показатель преломления 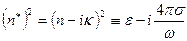 . Мы до сих пор не задумывались, почему материальные среды обладают дисперсией, то есть почему показатель преломления зависит от частоты, почему существуют области аномальной дисперсии и т.п.
. Мы до сих пор не задумывались, почему материальные среды обладают дисперсией, то есть почему показатель преломления зависит от частоты, почему существуют области аномальной дисперсии и т.п.
Напоминание:
Нормальная дисперсия: 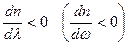 , или
, или 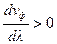 .
.
Аномальная дисперсия: 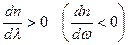 , или
, или 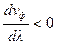 .
.
Для описания нормальной дисперсии Коши предложил формулу
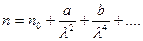
Достаточно большое число подгоночных параметров позволяет получить согласие с любым экспериментом.
Мы рассмотрим классическую (ºнеквантовую) теорию дисперсии;
Г.А. Лорентц: электроны и ядра подчиняются законам классической механики Ньютона.
В области не слишком высоких частот (не в рентгеновском диапазоне) колебания внутренних электронов не возбуждаются.
Собственная частота этой системы 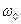 .
.
Почти неподвижный атомный остаток: 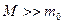 .
.
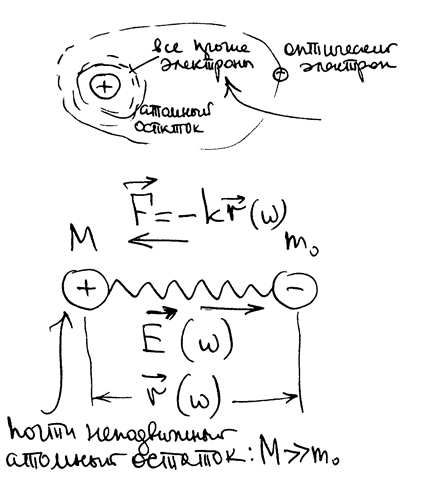 |
Модель упругого электрона или модель одного диполя (все атомы идентичны).
Рассматриваем газ, чтобы пренебречь взаимодействием между частицами.
Электрический дипольный момент каждой частицы 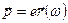 - по определению.
- по определению.
РИС.29-1
Полный момент единицы объема (поляризация):
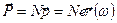 (
(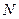 - концентрация частиц [см-3].
- концентрация частиц [см-3].
Вектор электрической индукции:
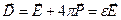 .
.
Отсюда: 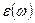 =1+4
=1+4 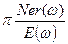 (в изотропной среде!).
(в изотропной среде!).
Поскольку 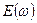 задано, задача сводится к вычислению
задано, задача сводится к вычислению 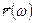 .
.
Используется классическое (т.е. неквантовое) уравнение движения:
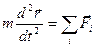 (будем полагать
(будем полагать 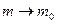 , так как
, так как 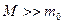
Вынуждающая сила
Со стороны электромагнитного поля на электрон действует сила 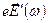 , где
, где 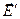 - локальное поле в точке, где находится электрон.
- локальное поле в точке, где находится электрон.
Разреженный газ – «полем Лорентца» можно пренебречь, считаем 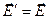 .
.
Магнитной компонентой в нерелятивистском приближении (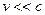 - в легких атомах) пренебрегаем, то есть
- в легких атомах) пренебрегаем, то есть  .
.
В тяжелых атомах 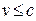 , и такое пренебрежение недопустимо.
, и такое пренебрежение недопустимо.
Возвращающая сила: 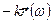 .
.
Тормозящая сила:  (например, потери энергии на излучение).
(например, потери энергии на излучение).
Итак, уравнение движения оптического электрона:
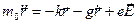 , где
, где 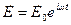 .
.
Поделим на 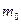 и перегруппируем члены:
и перегруппируем члены:
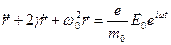 ,
, 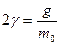 ,
, 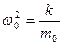 ,
, 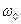 - собственная частота колебаний оптического электрона (УФ – видимый-ближний ИК).
- собственная частота колебаний оптического электрона (УФ – видимый-ближний ИК).
Заметим, что собственная частота колебаний ионов:
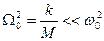 (дальний ИК).
(дальний ИК).
Решение уравнения ищем в виде:
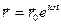 ,
, 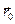 - равновесная позиция,
- равновесная позиция,
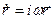 ,
, 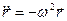 .
.
Подставляем:
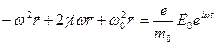 ,
,
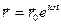 ,
,
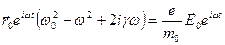 .
.
Амплитуда вынужденных колебаний электрона:
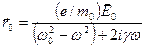 .
.
Движение оптического электрона происходит по закону
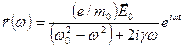 .
.
Полученный результат не является неожиданным:
1930 колебания происходят на частоте вынуждающей силы 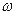 ;
;
1930 при 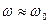 амплитуда колебаний максимальна;
амплитуда колебаний максимальна;
- движение происходит с ускорением, значит, заряженная частица излучает (поглощает) энергию.
Такой же результат получается (хотя иначе трактуется) и в квантовой механике. Существенно, что здесь (в квантовом методе) можно вычислить 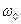 и
и 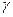 .
.
Поляризуемость среды
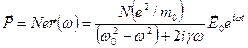 ,
,
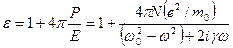 .
.
Простейший случай – отсутствие затухания,  ,
,  - дисперсия вдали от полосы поглощения:
- дисперсия вдали от полосы поглощения:
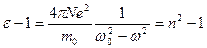
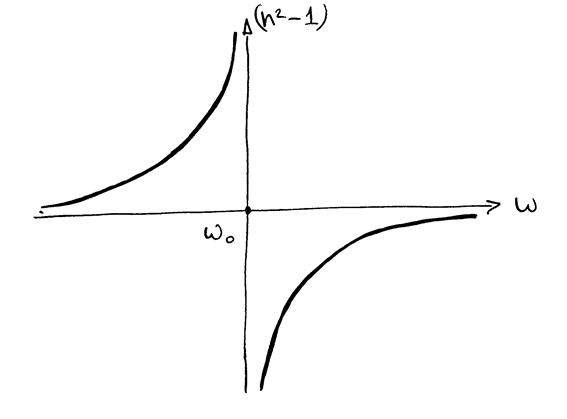 |
РИС.29-2
Разрыв непрерывности при 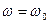 не отвечает физической реальности, поэтому рассмотрим по отдельности низкие частоты,
не отвечает физической реальности, поэтому рассмотрим по отдельности низкие частоты, 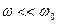 , и высокие частоты,
, и высокие частоты, 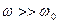 .
.
Низкие частоты: 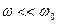 .
.
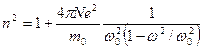 .
.
Так как 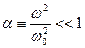 , то приближенно
, то приближенно 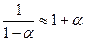 .
.
Получаем: 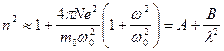 , где константы
, где константы 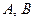 можно узнать из сравнения с экспериментом. Видно, что результат соответствует формуле Коши.
можно узнать из сравнения с экспериментом. Видно, что результат соответствует формуле Коши.
Высокие частоты: 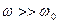 .
.
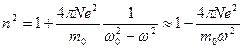 (
(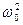 пренебрегаем).
пренебрегаем).
Для рентгеновских лучей (длина волны 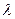 от 0.001 до 100 Å), то есть на очень высоких частотах электромагнитных волн, показатель преломления любого вещества близок к единице (немного меньше).
от 0.001 до 100 Å), то есть на очень высоких частотах электромагнитных волн, показатель преломления любого вещества близок к единице (немного меньше).
Стекло: 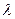 =1 Å,
=1 Å, 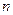 =1-10-6.
=1-10-6.
Обобщение
Если рассматриваемая система состоит из нескольких подсистем 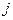 , каждая из которых характеризуется собственной частотой
, каждая из которых характеризуется собственной частотой 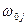 , то
, то
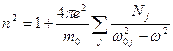 ,
,
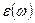 - сложная функция частоты.
- сложная функция частоты.
Это позволяет объяснить разницу между 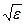 (
(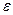 измеряется на одной частоте) и
измеряется на одной частоте) и 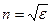 (
(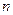 измеряется на другой частоте)
измеряется на другой частоте)
| Вещество | 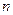
| 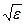
|
| Азот Толуол Вода | 1.000299 1.499 1.33 | 1.000307 1.549 |
| Видимая область спектра | Низкие частоты (МГц, кГц, иногда 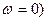
|
Аномальная дисперсия (учет затухания, комплексный показатель преломления)
(дополнительный материал)
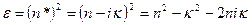 ,
,
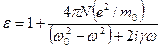 .
.
Числитель и знаменатель умножаем на 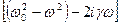 :
:
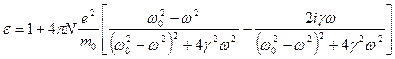 .
.
Приравнивая вещественную и мнимую части, получаем:
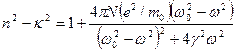 ,
,
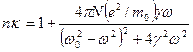 .
.
РИС.29-3
Учет локального поля (поля Лорентца)
(дополнительный материал)
Пора снова вспомнить, что на самом деле  .
.  складывается из внешнего поля
складывается из внешнего поля 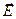 и поля окружающих частиц. В кубических кристаллах и в других конденсированных изотропных средах
и поля окружающих частиц. В кубических кристаллах и в других конденсированных изотропных средах 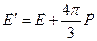 .
.
Рассмотрим движение в таком поле без учета затухания.
Уравнение движения:
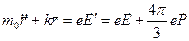 .
.
Умножаем правую и левую части на 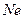 и вспоминаем, что
и вспоминаем, что 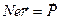 :
:
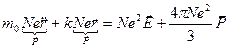 ,
,
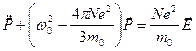 ,
,
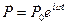 Þ
Þ 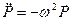 ,
,
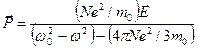 ;
;
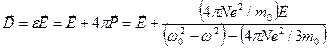 .
.
Отсюда: 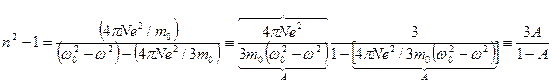 .
.
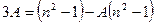 Þ
Þ 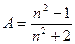 .
.
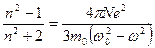 - формула Лоренца-Лорентца (Л.В. Лоренц, 1829-1891, - датский физик; Г.А. Лорентц, 1853-1928, - нидерландский физик).
- формула Лоренца-Лорентца (Л.В. Лоренц, 1829-1891, - датский физик; Г.А. Лорентц, 1853-1928, - нидерландский физик).
Date: 2015-05-08; view: 719; Нарушение авторских прав