
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Сложение колебаний, понятие о когерентности
|
|
При сложении двух гармонических колебаний одной частоты:
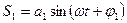
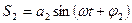
проходящих по одному направлению, получиться вновь гармонические колебания той же частоты:
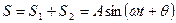
Найдем А и Q:
Представим колебания в виде вращающих векторов.
В момент времени t=0 проекция на оси x и у:
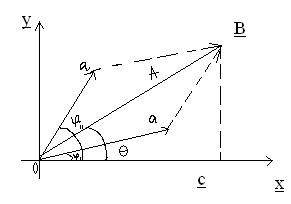
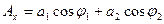
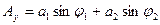
Тогда:
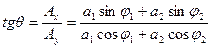
Тогда определяется θ.
Из 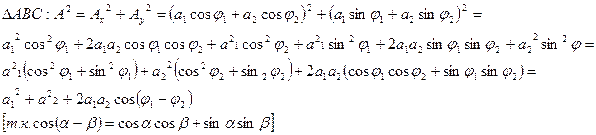
Таким образом, квадрат амплитуды результирующего колебания не равен сумме квадратов амплитуд складывающихся колебаний. Т.е. энергия результирующего колебания не равен сумме складывающихся колебаний. Результат сложения зависит от разности фаз 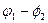 и может иметь любое значение от
и может иметь любое значение от 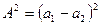 при
при 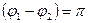 до
до 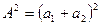 при
при 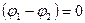
Практически мы никогда не имеем дела со строго гармоническими колебаниями. Обычно колебания времени от времени обрываются и возникают вновь уже с иной фазой. В таком случае и результирующая интенсивность 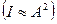 также меняется. Однако чтобы эти изменения зарегистрировать нужно, применить прибор, который реагировал бы достаточно быстро. Иначе мы будем реагировать только некоторое среднее во времени значение I (или <I>).
также меняется. Однако чтобы эти изменения зарегистрировать нужно, применить прибор, который реагировал бы достаточно быстро. Иначе мы будем реагировать только некоторое среднее во времени значение I (или <I>).
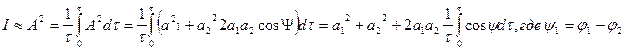 τ – интервал времени ~
τ – интервал времени ~ 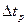 (время наблюдения)
(время наблюдения)
Если 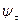 неизменно в течении времени наблюдения τ, то
неизменно в течении времени наблюдения τ, то 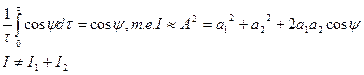

При случайных измерениях ψ
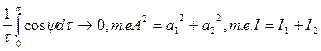
Таким образом, сложение 2-х колебаний надо различать два случая:
1.Разность фаз сохраняется неизменной за время τ достаточное для наблюдений. Тогда 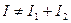 и колебания называются когерентными. Сложение колебаний, при котором не имеет места суммирование интенсивностей, называется интерференцией.
и колебания называются когерентными. Сложение колебаний, при котором не имеет места суммирование интенсивностей, называется интерференцией.
2.Разность фаз беспорядочно меняется за время наблюдения. 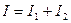 .
.
Колебания некогерентные
Таким образом, мы говорим об интерференции волн, когда при их совместном действии не происходит суммирование интенсивностей. Условием интерференции является их когерентность, т.е. сохранение неименной разности фаз за время, достаточное для наблюдений.
Результат интерференции определяется разностью фаз интерферирующих волн в месте наблюдения, а эта разность зависит от разности фаз и от разности расстояний, отделяющих точку наблюдения от источников каждой из волн.
Пусть волны имеют одинаковую линейную поляризацию. Т.к. 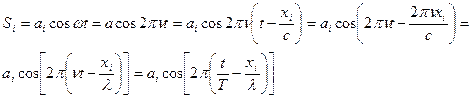
То для 2-х когерентных волн, имеющих одинаковые амплитуды.
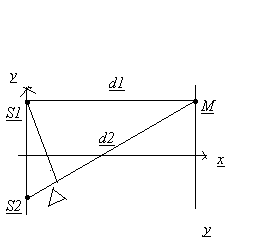

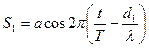
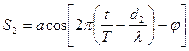 , где φ начальная разность фаз.
, где φ начальная разность фаз.
В точке М 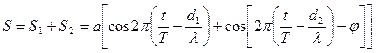
Т.к. 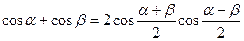
 , то
, то
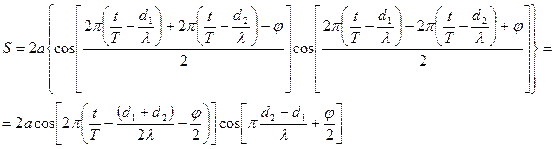
Таким образом, в точке М амплитуда будет:
 ,
,
А интенсивность:
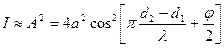 .
.
Так как для когерентных волн 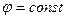 , то различие интенсивности света в разных точках зависит только от разности хода
, то различие интенсивности света в разных точках зависит только от разности хода 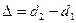 . Выразим разность хода через длину волны
. Выразим разность хода через длину волны 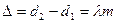 . Пусть φ=0 тогда
. Пусть φ=0 тогда 
целые m 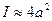
полу целые m 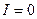
Таким образом, в зависимости от разности хода в различных точках будут получаться различные I.
Отметим, что точки, соответствующие постоянной разности хода располагаться на гиперболах. Но точечные источники излучают во все стороны. Но точечные источники излучают во все стороны. Поэтому пространственная картина интерференции обладает круговой симметрией относительно оси у. Таким образом, поверхности содержащие точки с постоянной Δ являются гиперболоидами вращения. На экране в плоскости х=Д получиться семейство гипербол, а на экране в плоскости у=Д получается окружности.
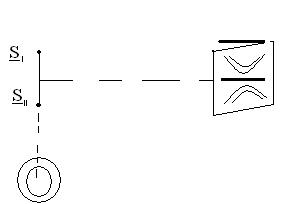
Временная и пространственная когерентность
Два идеально монохроматических колебания одной ν всегда когерентны и интерферирую. В противоположность этому колебания, разность фаз которых меняется беспорядочно и быстро - когерентны (или частично когерентны).
Если разность фаз 2-х колебания меняется достаточно медленно, то говорят, что колебания остается когерентными в течение некоторого времени пока их разность фаз не успела измениться на величину сравнимую с π.
Можно также сравнивать фазы одного и того же немонохроматического колебания в разные моменты 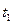 и
и 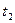 разделенные интервалом
разделенные интервалом 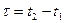 . Если немонохроматичность колебания проявляется в случайном изменении во времени его фазы, то при достаточно большом τ случайные изменения фазы колебания могут превысить π. Т.е. через время τ колебания как бы «забывает» свою первоначальную фазу и становится некогоретными, т.е. одна его часть теряет способность интерферировать с другой. Время τ в этом случае называется временем когерентности.
. Если немонохроматичность колебания проявляется в случайном изменении во времени его фазы, то при достаточно большом τ случайные изменения фазы колебания могут превысить π. Т.е. через время τ колебания как бы «забывает» свою первоначальную фазу и становится некогоретными, т.е. одна его часть теряет способность интерферировать с другой. Время τ в этом случае называется временем когерентности.
В случае эл/м волны (света) распределение электрического поля движется со скоростью волны. Для плоской немонохроматической волны распределения эл. поля в пространстве можно описать синусоидой с переменной амплитудой и фазой, которая в какой- либо точке пространства сохраняется только в течение времени когерентности τ. За это время волна распространяется на расстоянии с τ. Таким образом колебания поля Е в точках, удаленных друг от друга на расстоянии с τ вдоль распространения волны оказываются некогерентными (т.е. длина когерентности). Например, солнечный свет имеет длину цуга 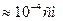 . Для лазерного излучения ~ км.
. Для лазерного излучения ~ км.
Все сказанное справедливо для плоской волны. В реальных волнах амплитуда и фаза меняется и в плоскости перпендикулярно направленному распространяются. Когерентность колебания исчезает на расстояние L, когда случайные изменения фаз в точках сравнимы с π. Таким образом, пространственная когерентность.
Объем когерентности ≈ длина цуга площадь круга диаметром L. Например, у поверхности излучающего тела ≈ несколько длин волн. По мере удаления от источника волна→ к плоской. Таким образом, степень пространственной когерентности возрастает ~ 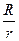 , где r – размер; R- расстояние до источника.
, где r – размер; R- расстояние до источника.
У лазерного излучения объем когерентности в 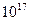 раз больше чем у не лазерного.
раз больше чем у не лазерного.
Интерференция света
Наблюдая отражение белого света от тонких, прозрачных пленок. Можно заметить, что их поверхности имеют характерную радужную окраску.
Явление, возникающее при сложении световых волн в пространстве и состоящее в том, что интенсивность результирующей световой волны в различных точках может быть больше или меньше суммы их интенсивностей, называется интерференцией света.
Методы наблюдения интерференции в оптике.
Из сказанного выше ясно, что интерференция наблюдается инерционным преемником излучения в области перекрытия 2-х когерентных световых пучков. Для их создания нужно в объеме когерентности выделить два вторичных источника света и с помощью того или иного способа осуществить наложение этих пучков. Тогда в области перекрытия, там, где разность хода не превышает длину когерентности. Будет наблюдаться интерференция.
В случае использования тепловых источников света для получения когерентных источников применяются два метода: метод деления амплитуды и метод деления фронта волны.
Суть метода деления амплитуды в следующем: свет т источника попадает на светоделительную пластину. Отраженные и проходящие лучи света имеют одинаковые амплитуды. Так как лучи образовались из деления одного и ТОО же цуга волны, то они когерентны. С помощью оптических устройств (например, зеркал) пучки перекрывают в некоторой области пространства. Если разность хода меньше длины когерентности, то наблюдается интерференция.
Например, интерферометр Майкельсона.
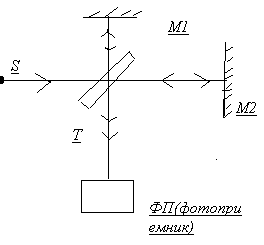
Интерферометр Маха-Цендера.
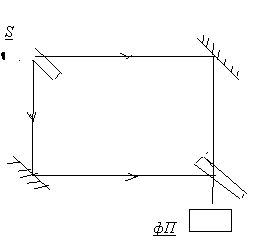
Интерферометр Жамена
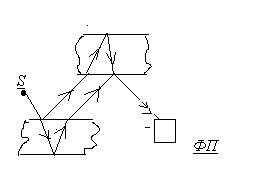
В каждой из этих схем луч света луч света делиться при отражении от поверхности двух сред на две части, затем создается с помощью оптических элементов и конструкции системы задержки между лучами.
В методе деления фронта волны когерентные излучатели получаются с помощью тех или иных оптических устройств, например, отверстий, линз, зеркал и т.д. расположенных на поверхности фронта волны. Важно, чтобы эти устройства не выходили за пределы в пространстве за пределы объема когерентности.
Например, опыт Юнга.
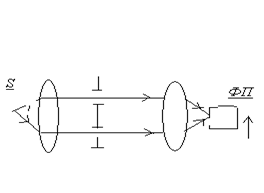
При измерениях фотоприемник перемещается в направлении стрелки.
Схемы с использованием бипризмы Френеля:
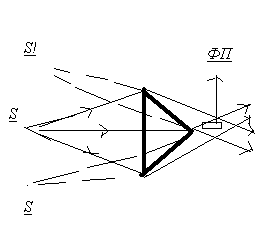
Бизеркала Френеля:
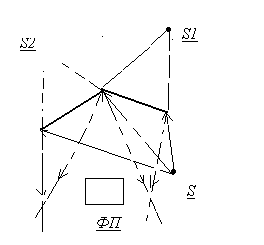
Билинза Бийе:
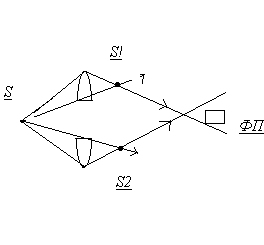
Общим для этих схем получение от реального источника S двух когерентных источников 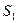 и
и 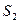 , которые располагаются на некотором расстоянии 2ив друг от друга и от которых на экране расположенном на расстоянии L от этих источников, наблюдается интерференционная картина.
, которые располагаются на некотором расстоянии 2ив друг от друга и от которых на экране расположенном на расстоянии L от этих источников, наблюдается интерференционная картина.
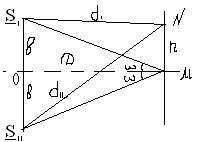 Пусть
Пусть 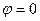 , то максимум т точке
, то максимум т точке 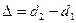
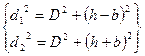
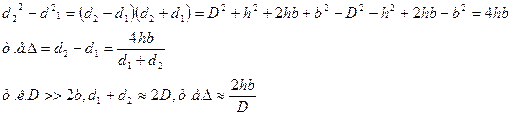
Если свет монохроматичен, то 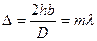
Интенсивность: 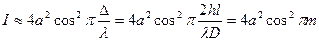
Расстояние между соседними max и min соответствующее изменению m на единицу 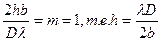 называется шириной полосы.
называется шириной полосы.
Интерференция в тонких пленках.
В пространстве около источников наблюдается интерференционная картина в виде совокупности гиперболоидов вращения.

Каждый гиперболоид будет соответствовать определенной разности хода mλ.
В зависимости от расположения экрана картина будет иметь вид полос, системы окружностей или частей гипербол.
Если размер источников увеличить, то пространственная область, где может наблюдаться картина, будет уменьшаться.
Если очень протяженный источник (небо), то, казалось бы, интерференционной картины не должно быть. Однако на тонких пленках (масло на асфальте, мыльная плёнка) глазом можно наблюдать интерференционную картину. Особенностью интефереционных полос является то, что они локализованы на поверхности.
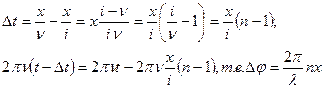
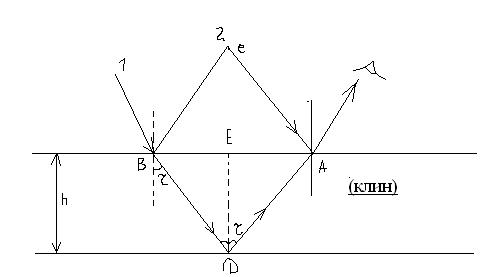
В пленке скорость света в n раз меньше чем в вакууме, где n показатель преломления. Поэтому после прохождения длины L фаза измениться на 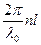 , где
, где 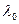 длина волны в вакууме.
длина волны в вакууме.
Величина 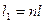 называется оптической длиной пути. Кроме подсчета разности оптических длин надо учесть, что при отражении света от среды с большим n фаза отраженной волны меняется на π, что равносильно т изменению пути на
называется оптической длиной пути. Кроме подсчета разности оптических длин надо учесть, что при отражении света от среды с большим n фаза отраженной волны меняется на π, что равносильно т изменению пути на 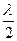 . Тогда:
. Тогда:
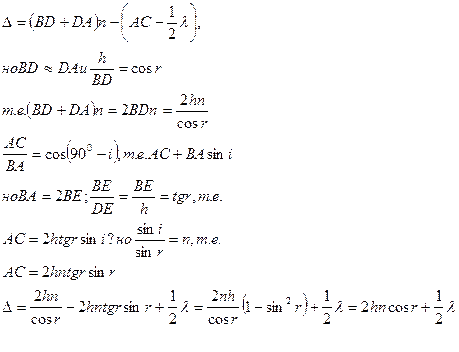
При наблюдении интерференционной картины глазом: из-за малости отверстия его зрачка происходит резкое ограничение по углу лучей, попадающих от протяженного источника света после отражения от пленки в глаз наблюдателя. Можно считать поэтому, что при определенном положении наблюдателя cosr является const. В этом случае картина интерференции зависит только от толщины пленки, т.е. толщины клина в точке.
При малых углов I (и соответственно r)разность хода Δ световых пучков излучаемых и другими точками протяженного источника, будет в точке А примерно такой же. Таким образом, в точке А на поверхности клина (или вблизи неё) интерференционные картины, создаваемые различными парами световых лучей приходящими от разных точек светящейся поверхности источника будут ≈ совпадать. Отсюда вытекает высокая видимость интерференционной картины на поверхности клина. В других областях над клинами будет иметь место беспорядочное положение различных интерференционных картин, и, следовательно, однородная освещенность этих областей пространства. Другими словами получает объяснение локализация интерференционной картины вблизи поверхности клина.
Освещенность всех точек интерференционной картины соответствующих одинаковыми толщинами h будет одинаковой (полосы одинаковой толщины).
Поскольку малейшее изменение h влияет на интерференционную картину – это наводит на мысли о возможности использования интерференционных эффектов для измерения малых смещений отражающих поверхностей.
В случае плоскопараллельной пластинки h и n всюду один и тот же и Δ может меняться только при изменении угла наклона лучей. Очевидно, что все лучи соответствующих одному и тому же значению r будет давать одну и ту же разность фаз, таким образом, max и min будут располагаться по направлениям, соответствующим одинаковому наклону лучей.
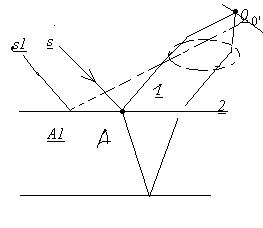 лучи 1и 2 отразившиеся от верхней и нижней граней будут параллельны друг к другу, так как пластинка плоскопараллельная. Поэтому интерференция будет наблюдаться в ∞. Для наблюдения надо аккомодировать глаз на бесконечность или собрать лучи линзой.
лучи 1и 2 отразившиеся от верхней и нижней граней будут параллельны друг к другу, так как пластинка плоскопараллельная. Поэтому интерференция будет наблюдаться в ∞. Для наблюдения надо аккомодировать глаз на бесконечность или собрать лучи линзой.
Лучи А1иS1 наклоненные под другим углом соберутся в другой точке фокальной плоскости.
Двухлучевые интерферометры.
Применяются для измерения малых разностей расстояний или малых изменений оптических свойств среды.
Один из простейших 2-x толстых плоскопараллельных пластин. при раздвоении луча в точке А возникает разность хода.
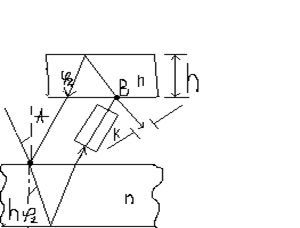 здесь h=20мм.
здесь h=20мм.
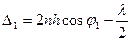 при схождении лучей в точке В добавляется разность хода
при схождении лучей в точке В добавляется разность хода 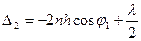
Если пластины одинаковые, то в случае их параллельности полная разность хода=0.
Если между пластинками образован малый угол ε, то 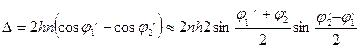
Обозначим 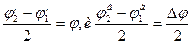 ; так как
; так как 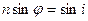 , то дифференцируя, имеем
, то дифференцируя, имеем 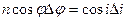 , т.е.
, т.е.
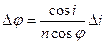
При обычных случаях 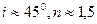
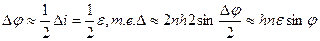
Таким образом, чем меньше ε, тем дальше отстоят друг от друга соседние max. Малейшим изменением углового распространения одного из лучей меняет интерферируя картину.
Например, помещая кювету к длины L и закачивая газ с ħ разность хода лучей измениться на 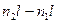 , где
, где 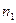 для воздуха. Если
для воздуха. Если 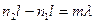 , то вся картина сместиться на m поло. По смещению можно определить
, то вся картина сместиться на m поло. По смещению можно определить 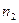 . Можно заметить изменения
. Можно заметить изменения 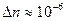 .
.
Интерферометр Майкельсона:
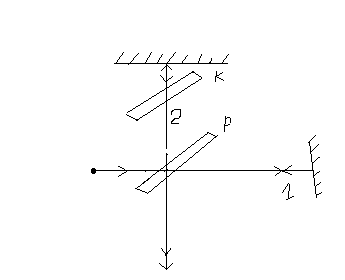
Пластинка Р покрыта полупрозрачным слоем.
1-ый луч проходит пластинку трижды, а 2- ой луч – один раз. Для компенсации этого ставиться пластинка к.
Если сместить одно зеркало на Δh, то возникает дополнительная разность хода =2Δh. Интерферометр обладает большой чувствительностью. С его помощью исследовалось влияние движения Земли на скорость света. На нем же сравнивалось длина эталонного метра с длиной световой волны: на 1 м укладывается 1650763,73 длины волны оранжевой спектр, линии криптона.
Этим прибором можно измерить длину когерентности перемещая одно из зеркал до исчезновения интерференции.
Например, пары кадмия дают излучение с длиной когерентности ~ 20см. С помощью 2-х лучевых интерферометров можно измерить и пространственную когерентность, например в схеме Юнга.
Многолучевые интерферометры – используются многократная интерференция нескольких световых лучей, что представляет практические преимущества. В частности, можно создать оптические устройства, пропускающие излучение лишь вблизи строго определенной частоты, т.е. интерференционные светофильтры.
Наиболее распространенный интерферометр Фабри-Перо. В частности он применяется в качестве оптического резонатора в лазерах.
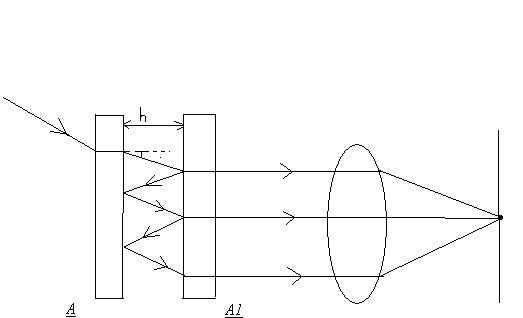
Поверхности пластинок или серебриться, или покрывается диэлектрическими пленками для высокого коэффициента отражения.
При освещении широким пучком света наблюдается система дифракционных колец.
Для одного из лучей при каждом отражении часть излучения выходит из резонатора в одном направлении.
Если их всех собрать линзой, то в фокусе результирующее поле будет определяться суммой полей прошедших лучей.
[ разность хода между двумя соседними пуками в эталоне Фабри – Перо
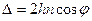 главный максимум при
главный максимум при 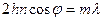 . Оценим порядок максимума, положив
. Оценим порядок максимума, положив 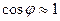
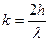
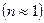 воздух
воздух
Например, h=0,5, λ~ 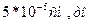 к=20000
к=20000

На кольцо длины волны  λ, и порядка к належится кольцо с
λ, и порядка к належится кольцо с 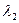 , порядка к-1. если
, порядка к-1. если 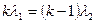 т.е.
т.е.
 постоянная эталона.
постоянная эталона.
Т.е. 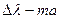 разность длин волн, при котором система колец одной длины волны перекрывается системой колец другой длины волны.
разность длин волн, при котором система колец одной длины волны перекрывается системой колец другой длины волны.
Например, при h=0,5 см, λ~ 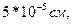
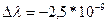
Только такой узкий участок спектра можно исследовать без наложения колец разных порядков.
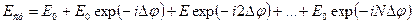
Если считать амплитуды всех лучей одинаковыми, то получается сумма геометрической прогрессии и
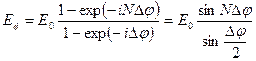 где
где 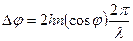
Max при 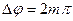 , первый min
, первый min 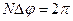 } это определяет ширину интерфер. полосы в зависимости от λ.
} это определяет ширину интерфер. полосы в зависимости от λ.
Изменение разности хода на 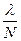 определяет ширину полосы интерференции. Таким образом, интерферометр оказывается высокоточным измерительным длины.
определяет ширину полосы интерференции. Таким образом, интерферометр оказывается высокоточным измерительным длины.
Принцип Гюйгенса-Френеля
Наблюдения за прохождением света через непрозрачный экран с отверстием выявляет следующее: Если размер отверстия >> λ волны, то свет распространяется за экраном по прямой и дает изображение отверстия на втором экране. При уменьшении отверстия изображение отверстие так же будет уменьшаться, однако, до определенного предела.
Как только размер отверстие становиться сравнимым с λ света, наблюдается огибание светом препятствия - размер изображения отверстия начинает увеличиваться при его сужении.
Явление отклонение света от закона прямолинейного распространение при прохождении через экраны называется дифракцией.
Отклонение света от прямолинейного направления распространения происходит и в тех случаях, когда на его пути находится небольшая преграда или среда, показатель преломления который завит от координат. Таким образом, дифракция наблюдается всегда, когда свет проходит через среду или экран с оптическими неоднородностями.
С точки зрения эл/м теории явлении дифракции объясняется тем, что распространение света подчиняется волновому уравнению, при существовании каких-либо препятствий в пространстве однородность условий распространения эл/м волн нарушается, следствием его и является дифракцией.
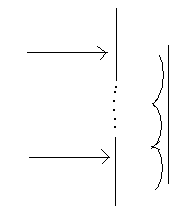
Впервые дифракцию с волновой точки зрения рассмотрел голландский физик Х.Гюгенс. Сформулированный им принцип: Пусть возмущения (волна) распространяется в некотором направлении и известно положение волнового фронта в некоторый момент t, а также скорость распространения волны c.
Примем каждую точку фронта за источник вторичных волн. Посмотрим элементарные волны радиуса 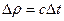 и проведем огибающею их поверхностей. Она и определит положение фронта в момент
и проведем огибающею их поверхностей. Она и определит положение фронта в момент 
Этот принцип нечего не говорит о распространении амплитуд по фронту волну.
Французский физик Френель (1788-1827) дополнил принцип Гюйгенса, предложив, учитывать интерференцию вторичных волн и разработал, для этого метод расчета. Френель не только рассчитывал дифракционные задачи, но объяснить прямолинейность распространения света в свободном пространстве, что было триумфом нового метода и способствовало всеобщему признанию волновой теории света.
Последующие исследования Максвелла, Киргофа, Грина позволили обосновать представления Гюйгенса – Френеля и показали, что по существу он является одним из методов решения волнового уравнения с заданными граничными условиями.
Дифракция света Френеля и Фраунгофера
Зоны Френеля.
Рассмотрим действия световой волны, испущенной из А в какой-нибудь точке наблюдения В. Согласно принципу Гюйгенса – Френеля заменим действия источника А действием воображаемых источников, расположенных на вспомогательной поверхности S(поверхность фронта волны идущей из А) 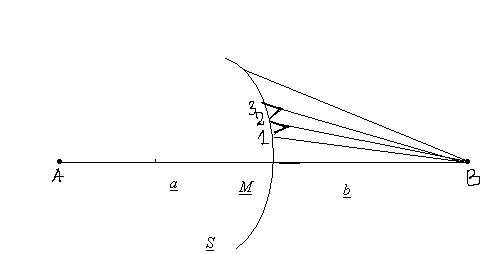
Вычисления результата интерференции вторичных волн очень упрощается, если для вычисления действия в точке В разбить поверхность S на зоны такого размера, чтобы расстояние от краев зоны отличались на 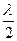 .
.
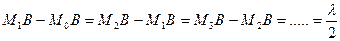
Для первой зоны:

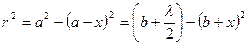
Или 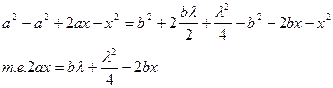
 ; так как λ>> а;в то пренебрежение числом с
; так как λ>> а;в то пренебрежение числом с  :
:
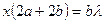 или
или 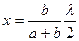
Площадь сегмента 1- ой зоны 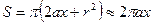 , так как r мало или:
, так как r мало или:
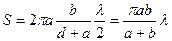
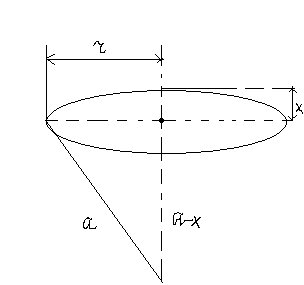
Площадь 2-ой зоны:

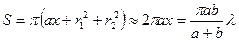
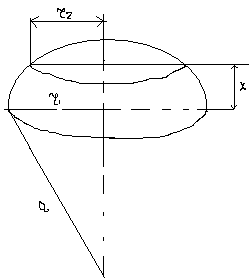
Следующие зоны тоже имеют такую же площадь. Таким образом, площадь(поверхность)сферической волны разбирается на одинаковые по площади зоны в В есть 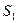 , соседний
, соседний 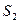 и т.д.
и т.д.
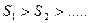 так как угол φ разный. Благодаря выбранному способу разбиения действия соседних зон ослабляют друг друга, так как
так как угол φ разный. Благодаря выбранному способу разбиения действия соседних зон ослабляют друг друга, так как 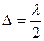 (противофазе).
(противофазе).
Окончательное значение амплитуды в В будет 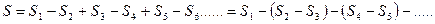
в скобках выражение>0. поэтому 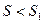 таким образом, действия всей волны в В сводиться к действию её малого участка (<центральной зоны с площадью
таким образом, действия всей волны в В сводиться к действию её малого участка (<центральной зоны с площадью 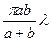 ).
).
Так как 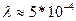 мм, то даже для а и b ~1мм площадь действующей части волны
мм, то даже для а и b ~1мм площадь действующей части волны 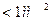 . Таким образом, распространение света от А и В происходит так, как если бы световой поток шел внутри очень узкого канала (прямолинейно).
. Таким образом, распространение света от А и В происходит так, как если бы световой поток шел внутри очень узкого канала (прямолинейно).
Но это не означает, что если на линии АВ поместить небольшой экран, то до В свет не дойдет. Например, если закрыть 1-ую зону, то выпадет 1- ый член ряда и окажется 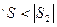 и т.д.,
и т.д., 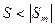 , где m номер первой открытой у экрана зоны.
, где m номер первой открытой у экрана зоны.
Если размер отверстия в непрозрачном круглом экране такой, что открытым остается четное число зон, то S→0 и в В будет «темнота». Изменение диаметра к периодическому усилению и ослаблению света при проходе от четного к несчетному числу открытых зон.
Более того, если перемещать точку наблюдения вдоль прямой АВ начав с расстояния на котором, например отверстие оставляют открытой одну зону и приближаться к экрану, то число открытых зон будет расти, а потому снова должны наблюдаться по переменные переходы от света к темноте.
Так как наибольшее значение суммы ряда получается если открыта одна зона, то это можно истолковать как получение изображения точечного источника (камер-обскуры).
Полученные результаты можно сделать наглядными при помощи векторной диаграммы. Разобьем первую зону на большое число равновеликих кольцевых зон. Пусть колебания создаваемые частью зоны прилегающей к оси ОА изображаются вектором 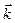 . Каждая следующая часть зоны создает колебания, изображаемые таким же по модулю вектором, повернутым на малый угол, учитывающий сдвиг фазы. Так как фазы колебания от центра и края 1-ой зоны сдвинуты на
. Каждая следующая часть зоны создает колебания, изображаемые таким же по модулю вектором, повернутым на малый угол, учитывающий сдвиг фазы. Так как фазы колебания от центра и края 1-ой зоны сдвинуты на 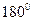 , получим половину правильного многоугольника (полуокружность)
, получим половину правильного многоугольника (полуокружность) 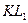 . Действия 2-ой зоны тоже полуокружность меньшего радиуса, так как амплитуда колебания уменьшается. Продолжая построение, получим спираль. Тогда амплитуда колебания в точке наблюдения изобразится отрезком КТ. Если же на пути световой волны экран с отверстием, на котором укладывается, например, одна или три зоны, то амплитуда колебаний будет
. Действия 2-ой зоны тоже полуокружность меньшего радиуса, так как амплитуда колебания уменьшается. Продолжая построение, получим спираль. Тогда амплитуда колебания в точке наблюдения изобразится отрезком КТ. Если же на пути световой волны экран с отверстием, на котором укладывается, например, одна или три зоны, то амплитуда колебаний будет 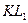 или
или  . Напротив, при четном числе зон амплитуды
. Напротив, при четном числе зон амплитуды 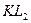 и
и 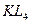 оказываются малыми.
оказываются малыми.
Зонная пластинка.
Очевидно, что если создать экран, перекрывающий излучений от всех честных или нечетных зон Френеля, он обеспечит значительное усиление интенсивность в точке наблюдения. Экран, функция пропускания которого обеспечивает перекрытия всех честных или нечестных зон Френеля, называется зоной пластинкой Френеля.
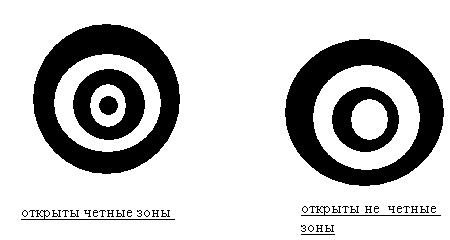
Если пластинку поставить на пути волны, то в точке В
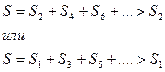
и освещенность возрастает по сравнению со случаем свободного распространения света.
Векторная диаграмма содержит только ε витков спирали.
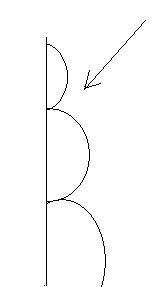 так как при изменении точки наблюдения условия оптимальной освещенности для данной зонной пластинки не выполняются, она создает значительную интенсивность света лишь в окрестности точки В для которой рассчитана. Поэтому зонная пластинка подобна собирающей линзе. Можно достичь еще большей яркости, если не зачернять зоны, а заставить их изменять фазу света на π (фазовая зонная пластинка).
так как при изменении точки наблюдения условия оптимальной освещенности для данной зонной пластинки не выполняются, она создает значительную интенсивность света лишь в окрестности точки В для которой рассчитана. Поэтому зонная пластинка подобна собирающей линзе. Можно достичь еще большей яркости, если не зачернять зоны, а заставить их изменять фазу света на π (фазовая зонная пластинка).
Простейшее дифракционные проблемы.
Будем пользоваться гипотезой положенной Френели в основу его рассуждений, пологая, что часть фронта волны прикрытия экраном не действует совсем, а неприкрытые участки действуют так, как если бы экрана порядка λ. Но при достаточно больших отверстиях влияния этой краевой зоны незначительно,
а) дифракция на кругом отверстии
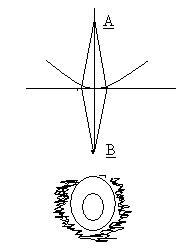
Разбивка на зоны Френеля покажет, что в зависимость от размера отверстия в нем уложится большее или меньшее число зон. Если открыто нечетное число зон, то действия в точке В больше чем в отсутствие экрана. Для точек плоскости 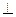 АВ вследствие симметрии всего расположения вокруг линии АВ распределение света должно симметрично, т.е. области одинаковой освещенности должны располагаться кольцеобразно около точки В.
АВ вследствие симметрии всего расположения вокруг линии АВ распределение света должно симметрично, т.е. области одинаковой освещенности должны располагаться кольцеобразно около точки В.
Если отверстие открывает нечетное число зон, то в центре светлое пятно. Если четное, то в центре экрана темнота.
б) Дифракция на круглом экране
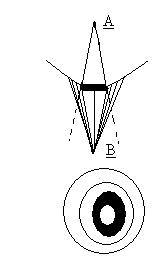
Если размер экрана мал то действие 1-ой открытой зоны почти не отличается от действия центральной зоны волнового фронта. Таким образом, освещенность в В будет ≈ такой же как и в отсутствии экрана. Вследствие симметрии относительно АВ светлая точка в В окружена кольцевыми зонами тени и света (вне границ геометрической тени).
в) Дифракция на краю полубесконечного экрана.
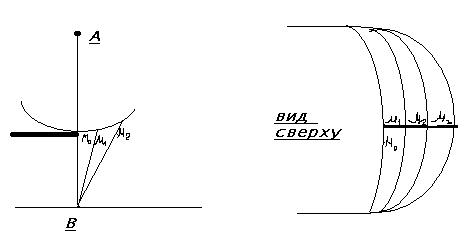
Решаем задачу путем разбиения поверхности волны на зоны так, что 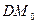 ,
, 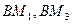 отличаются на
отличаются на 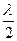 и затем из A проведем плоскости параллельные ребру экрана через
и затем из A проведем плоскости параллельные ребру экрана через 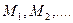
Площади таких лупок относятся как 1:0,41:0,32:0,27:0,22…..
Векторная диаграмма для точки В на линии перпендикулярна краю экрана.
По мере того как точка В будет смещаться параллельно экрану в сторону освещенной части пространства. Будет открываться новые зоны. Если удалиться от края экрана так, что его действие можно не учитывать, то векторная диаграмма будет спиралью Корню.
Дифракция Фраунгофера.
До сих пор мы рассматривали дифракцию сферическую (или плоских) волн и изучали дифракционную картину на конечном расстоянии от препятствия (дифракция Френеля). При больших удалениях от экранам с неоднородного (например, со щелью), на поверхности щели уложиться лишь часть первой зоны Френеля. Тип дифракции, при котором рассматривается дифракционная картина образованная параллельными лучами называется дифракцией Фраунгофера. Например
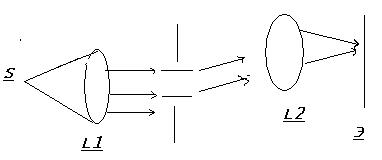
Такой тип дифракции можно рассматривать математически до конца.
Помещая между линзами разные экраны, мы меняем характер дифракционной картины, являющейся изображение источника.
Дифракция на щели.
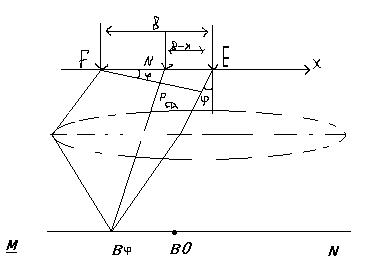
Пусть волна попадает нормально к площади щели. Разобьем площадь щели на ряд узких полосок равной ширины. Каждая из них может рассматриваться как источник волн, причем фазы всех этих волн одинаковы. Амплитуды также одинаковы. Это упрощает решение задачи.
Графически результат сложения амплитуд для любой точки экрана:
а) 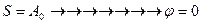 . При
. При 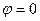 элементарные волны не приобретают никакой разности фаз. Результирующая амплитуда
элементарные волны не приобретают никакой разности фаз. Результирующая амплитуда 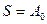
б) 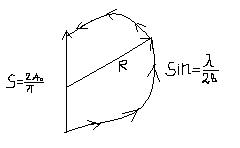 направление φ при котором крайние элементы волнового фронта в пределах щели дают разность фаз =π, т.е разность хода =
направление φ при котором крайние элементы волнового фронта в пределах щели дают разность фаз =π, т.е разность хода = 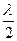 .т.е
.т.е 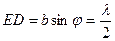 .
.
Так как амплитуда от всей щели = 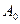 или
или 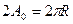 по
по 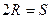 - к вектору амплитуды, т.е.
- к вектору амплитуды, т.е. 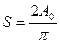 .
.
в) 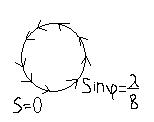 если разность хода лучей от краев щели =λ, т.е. соответствует
если разность хода лучей от краев щели =λ, т.е. соответствует 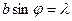 , то S=0. Нетрудно видеть, что S=0 и для разностей хода 2 λ,3 λ,….,т.е.min соответствует направлениям
, то S=0. Нетрудно видеть, что S=0 и для разностей хода 2 λ,3 λ,….,т.е.min соответствует направлениям
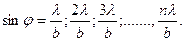


 разобьем щель на полоски и изобразим цепочку соответствующих элементарных векторов для определенного угла дифракции φ. Так как
разобьем щель на полоски и изобразим цепочку соответствующих элементарных векторов для определенного угла дифракции φ. Так как 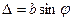 , то разность фаз
, то разность фаз 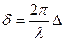 .
.
Последний вектор цепочки относительно 1- ого повернуть на угол 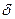 .
.
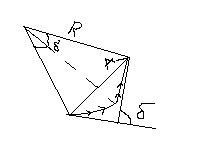 длина цепочки =
длина цепочки = 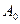 (амплитуда подающего света)
(амплитуда подающего света)
А – результирующий вектор, 2πR- длина всей окружности, 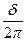 - часть окружности изображенной на рисунке. Её длина будет
- часть окружности изображенной на рисунке. Её длина будет 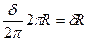 но это =
но это = 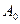 , т.е
, т.е 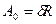
Из Δ получим 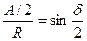 , т.е.
, т.е. 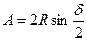 но
но 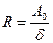 ,т.е.
,т.е. 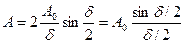 отсюда
отсюда
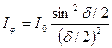 , но
, но 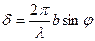
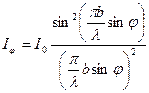
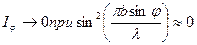 т.е.
т.е. 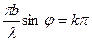 или
или
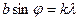
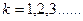
Для аналитического расчета интенсивности света щелью, напишем выражение для волны, посылаемый каждым элементом волнового фронта и просуммируем действие всех элементов. Амплитуда волны от одного элемента ~ его ширине dx, т.е = cdx. Величину с найдем из условия, что в направлении φ=0 амплитуда воны = 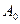 или cb=
или cb= 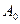 .т.е.
.т.е. 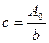 . Таким образом, возмущения в соответствующем участке щели
. Таким образом, возмущения в соответствующем участке щели 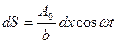
Для отыскания действия всей щели в направлении φ надо учесть разность фаз, характеризующую волны, доходящие от разных элементов волнового фронта до 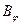 .
.
Проведем плоскость FD перпендикулярно к направлению нормалей дифрагировавших волн.
Разность хода от А и от N есть 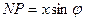 . Тогда световое возмущение в точке Р будет
. Тогда световое возмущение в точке Р будет 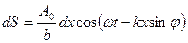 , где
, где 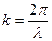 волновое число.
волновое число.
Результирующее возмущение в точке 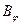 определиться как сумма этих выражений:
определиться как сумма этих выражений:
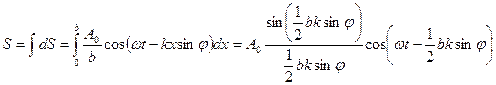 . Таким образом, амплитуда волны в направлении φ
. Таким образом, амплитуда волны в направлении φ 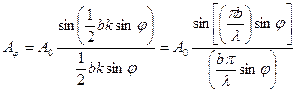 (*)
(*)
Так как обычно φ мал, то 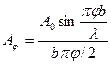 т.е вдоль экрана с изменением φ освещенность меняется проходя через min и max.
т.е вдоль экрана с изменением φ освещенность меняется проходя через min и max.
Из (*) следует, что  для углов φ удовлетворяющему условию
для углов φ удовлетворяющему условию 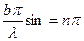 ,
, 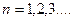 или
или 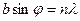 наибольший max при:
наибольший max при: 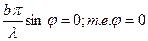 тогда
тогда 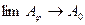 из (*)
из (*)
Следующие max, получаем из условия экстремума 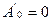 .
.
Расчет дает 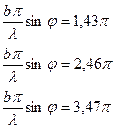
Численные значения интенсивностей главного и следующих max относиться как 1:0,045=0,016….
В первом приближении можно считать угловые max более простым 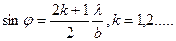 в случае b>>λ решение (Рэлей 1897)и для b~λ Морзе и Рубинштейн (1938).расчеты полученному и потому нет заметных ошибок для дифракционных решеток.
в случае b>>λ решение (Рэлей 1897)и для b~λ Морзе и Рубинштейн (1938).расчеты полученному и потому нет заметных ошибок для дифракционных решеток.
Дифракционная решетка
Например, две щели дадут одинаковые, накладывающиеся друг на друга дифракционные картины.
За счет этого max усилится. Однако, картина сложнее, т.е. надо принять во внимание взаимную интерференцию волн идущих от 1-ой и 2-ой щели.
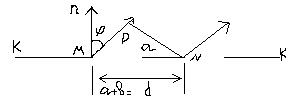 Очевидно, min будет на тех же местах, т.е. те направления, по которым ни одна из щелей не посылает света не получит его и при 2-х щелях. Кроме того, возможны направления, в которых колебания, посылаемые двумя щелями, взаимно уничтожаются, т.е. направления которым соответствует разность хода
Очевидно, min будет на тех же местах, т.е. те направления, по которым ни одна из щелей не посылает света не получит его и при 2-х щелях. Кроме того, возможны направления, в которых колебания, посылаемые двумя щелями, взаимно уничтожаются, т.е. направления которым соответствует разность хода 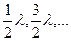 для волн идущих от соответственных точек обеих щелей. Например,
для волн идущих от соответственных точек обеих щелей. Например,
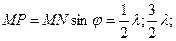 т.е.
т.е. 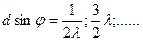
Наоборот, в направлениях 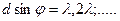 действие одной щели усиливает действие другой, т.е главный max.
действие одной щели усиливает действие другой, т.е главный max.
Полная картина:
Прежнее min 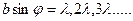
Добавочные min 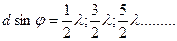
Главный max 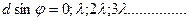
т.е. между двумя главными max будет становиться уже, чем от одной щели.
Система параллельных щелей называется дифракционной решеткой. Величина d=a+b называется постоянной решетки 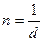 число штрихов на единицу длины (n больше или равен 2000)
число штрихов на единицу длины (n больше или равен 2000)
С учетом того, что разность фаз между колебаниями от соседних щелей.
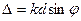 . Амплитуды волны вместо (*) будет иметь:
. Амплитуды волны вместо (*) будет иметь: 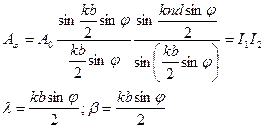
Таким образом, распределение интенсивности в дифракции картине зависит от 2-х сомножителей. Первый определяет дифракцию на одной щели. А второй – взаимодействие лучей от отдельных щелей.

В отличии от дифракции на одной щели, дифракционная картина на N щелях характеризуется наличием острых max которые наблюдаются при условии  (т.е знаменfтиль в формуле для
(т.е знаменfтиль в формуле для  должен =0) или
должен =0) или 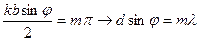 добавочные min будут при условии
добавочные min будут при условии  или
или
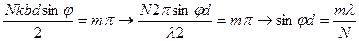
Общая картина:
Прежнее min 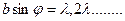
Главные max 
Добавочные min 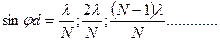 т.е между двумя главными max располагается
т.е между двумя главными max располагается  добавочных min. Вторичные max очень слабы <
добавочных min. Вторичные max очень слабы < 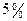 от главного.
от главного.
Угловые расстояния между главным max и соседним min определяется требованием. Чтобы разность хода взросла на 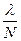 , т.е.
, т.е. 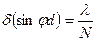 или
или  и
и 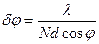
При небольших углах дифракции (cosφ≈1)резкость главных максимумов не зависит от порядка спектра и равна, 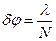 т.е. тем лучше. Чем больше λN. т.е общая ширина решетки.
т.е. тем лучше. Чем больше λN. т.е общая ширина решетки.
Разрешающая способность – возможность различить максимумы близких волн 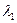 и
и 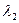 .
.
Для главного max 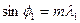
Условия min sin 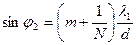
Если max второй волны виден под углом больше или меньше 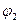 , то его можно увидеть.
, то его можно увидеть. 
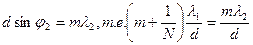 так как
так как 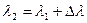 , то
, то 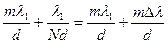 отсюда
отсюда 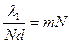 - разрешающая способность, определяется порядком (m) и числом штрихов (N).
- разрешающая способность, определяется порядком (m) и числом штрихов (N).
У лучших решеток ~ 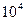 и возможно разделить две волны, длины волн которых отличаются на
и возможно разделить две волны, длины волн которых отличаются на 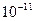 м.
м.
Существуют также фазовые решетки, позволяющие концентрировать до 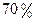 энергии в какой-либо ненулевой главной max (например, отражающие).
энергии в какой-либо ненулевой главной max (например, отражающие).
Дифракция рентгеновских лучей.
Большой интерес представляет дифракция на пространственных периодических структурах. Например, кристаллы, где можно наблюдать дифракцию рентгеновских волн, у которых λ соизмерима с межатомным расстоянием.
Впервые такой опыт поставлен по предложению Лауэ в 1912г. Причем оказалось, что за кристаллом на фотопластинке получилось центральное неотклонённое пятно и ряд закономерно расположенных пятен, распределенных в плоскости перпендикулярно от неотклоненного пучка рентгеновских лучей. Таким образом, случай дифракции на 3-х мерной решетке. Здесь открывается возможность определения λ ренгентовских лучей, если известна структура решетки кристалла, кроме того наблюдая дифракцию лучей с известной λ возможно найти структуру кристалла(рентгеноструктурный анализ). Но всё это представляет сложную стереометрическую задачу.
Ограничимся простейшим видом дифракции в отраженных лучах, рассчитанным Вульфом и Брэггом в 1913 г. Пусть расстояние между атомными слоями есть d. Падающие рентгеновские лучи рассеиваются на нескольких атомных плоскостях в различных направлениях. При интерференции рассеянных волн можно найти направления, где интенсивность будет наибольшей. Для этого надо, чтобы разность хода между лучами, отраженными от соседних атомных плоскостей = целому числу λ, т.е. 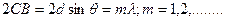
 где
где 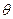 угол скольжения, дополняющей угол падения до
угол скольжения, дополняющей угол падения до 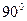 .
.
Дифракция на ультразвуковых стоячих волнах.
Пространственную решетку, на которой можно наблюдать дифракцию видимых световых волн можно осуществить на ультразвуковых волнах. Например, в пластинке кварца или турмалина можно возбудить колебания 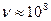 Гц.
Гц.
Поместив такую пластинку в жидкость (ксилол) получим ультраакустические волны в жидкости. Упругая волна в жидкости - это волна сжатая и разрежения, т.е. и различного показателя преломления. Поэтому для света получается фазовая решетка. Если заставить ультраакустическую волну отражаться от дна сосуда, то образуется стоячая ультраакустическая волна, которая представляет собой периодическую структуру переменной плотности с периодом = длине ультраакустической волны.
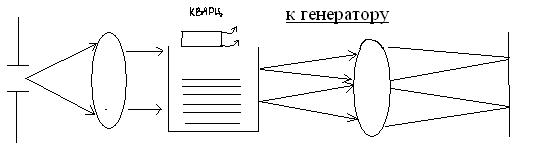
Например, в ксилоле скорость акустической волны 1000 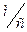 и при
и при 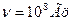 из
из 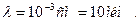 т.е. получается фазовая решетка периодом 10 мкм.
т.е. получается фазовая решетка периодом 10 мкм.
Если пустить ультраакустические волны по 3-м направлением, то получим пространственную решетку.
В таких решетках показатель преломления меняется еще и с периодом волны, т.е. 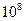 раз в секунду. Это приводит к модуляции интенсивности дифрагировавшего света. Т.е если на ультраакустическую волну попадает свет с
раз в секунду. Это приводит к модуляции интенсивности дифрагировавшего света. Т.е если на ультраакустическую волну попадает свет с 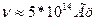 , то дифрагировавший свет будет иметь частоту
, то дифрагировавший свет будет иметь частоту 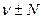 , где N частота ультраакустической волны ~
, где N частота ультраакустической волны ~ 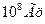 .
.
Излучение дифракции света на ультраакустических волнах - важный метод исследования законов распространения этих волн в веществе.
Понятие о голографии – метод восстановления изображений без линз предложил и осуществил в 1948 году английский физик (венгр) Денис Габор.
Фиксируется полная информация о распределения амплитуды и фаз, волновых полей в отличие от фотографического метода, где фиксируется только распределение в пространстве интенсивности! Но именно фазы волн содержат в себе информацию о взаимном расположении частей источника света, о его удалении от приемника и т.д.
На голограмме регистрируется не само изображение предмета, а структура световой волны отраженной предметом.
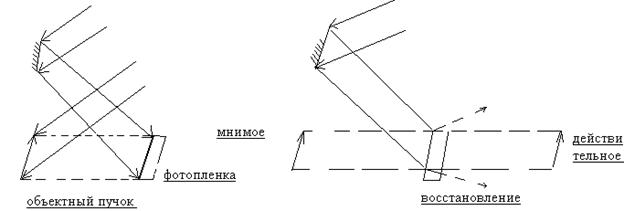
В 1962 году Ю.Н.Денисюк предложил метод регистрации голограмм в толстых Эмульсиях, толще, чем расстояние между полосами интерференции регистрируемого поля. Это позволяет получать объемную дифракционную решетку, при освещении которой можно восстановить даже спектр излучения. Это позволяет при считывании изображения использовать обычный свет.
Поляризация света
Из эл|.м теории света вытекает, что световые волны поперечны. Однако, вектора 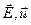 могут быть произвольно ориентированы относительно направления распространения волнового фронта (или луча). В оптике плоскость содержащую вектор
могут быть произвольно ориентированы относительно направления распространения волнового фронта (или луча). В оптике плоскость содержащую вектор 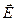 и вектор в направлении распространения называется плоскостью поляризации.
и вектор в направлении распространения называется плоскостью поляризации.
Плоскость же содержащую 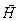 называется плоскостью колебаний. Эти плоскости взаимно перпендикулярны.
называется плоскостью колебаний. Эти плоскости взаимно перпендикулярны.
Электромагнитное излучение, у которого направления поля 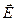 остается неизменным называется плоскопооляризованным (или линейнополяризованным). В пучке света некогерентного источника направлений электрического хаотически меняется по перпендикулярно
остается неизменным называется плоскопооляризованным (или линейнополяризованным). В пучке света некогерентного источника направлений электрического хаотически меняется по перпендикулярно 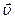 . такой свет называется неполяризованным.
. такой свет называется неполяризованным.
Date: 2015-05-08; view: 3669; Нарушение авторских прав