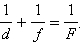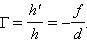Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Отражение и преломление света на сферической поверхности раздела
|
|
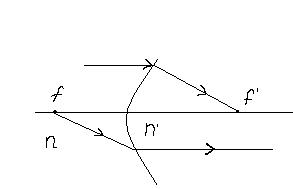
Будем рассматривать только те лучи, направление распространения которых с нормалью к поверхности составляет малые углы. Т.е. sin и tg можно заменить значениями углов (параксиальные лучи).
Введем прямоугольную систему координат с началом О на сферической поверхности. Тогда все расстояния, отчитываемые влево меньше О, а вправо больше О. Вертикальные отрезки отчитываемые вверх больше О, а вниз меньше О.
Углы меньше О если их sin меньше О.Если углы отчитываемые от нормали к сферической поверхности не совпадают с выбранной осью абсцисс, то больше нуля если поворот луча к нормали против часовой стрелки. 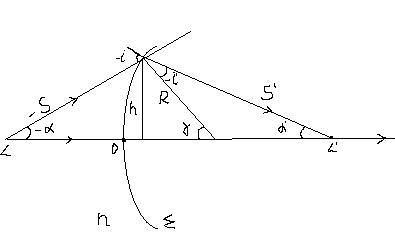
Рассмотрим преломление 2-х лучей: одного вдоль оси абсцисс и другого под углом ~ (-α). Первый луч не изменит направление. Второй падая под углом (-i)преломится под углом ~ (-i’). Причем для параксиальных лучей 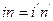 .
.
Так как i внешний в треугольнике, то 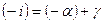 , т.е.
, т.е. 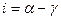
аналогично 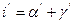 .
.
так как 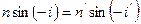 или
или 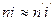 или
или 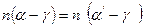
т.е. 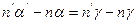 , но
, но 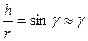 , отсюда
, отсюда 
а так как 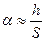 ;
; 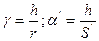 , то
, то 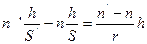 или
или 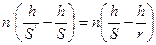
или же 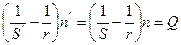 т.е. преломлении параксиальных лучей на сферической поверхности остается постоянной некоторая величина Q (инвариант Аббе).
т.е. преломлении параксиальных лучей на сферической поверхности остается постоянной некоторая величина Q (инвариант Аббе).
Преобразим полученное выражение:
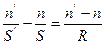 (*)
(*)
Если источник бесконечно далеко, т.е. 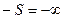 , то после преломления лучи собираются в точке называемой задним фокусом сферической поверхности
, то после преломления лучи собираются в точке называемой задним фокусом сферической поверхности 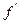 . Значение
. Значение 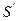 тогда
тогда 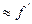 .
.
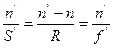
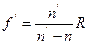
Если источник поместить в точку 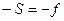 , т.е. в передний фокус сферической поверхности, то
, т.е. в передний фокус сферической поверхности, то 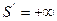 и лучи распространяются параллельно друг другу.
и лучи распространяются параллельно друг другу.
Причем 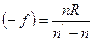 .
.
Величину, 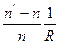 определяющую переднее фокусное расстояние называется оптической силой сферической поверхности.
определяющую переднее фокусное расстояние называется оптической силой сферической поверхности.
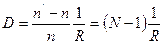 ; где
; где 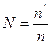
Если в (*) заменить n на 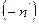 то получим формулу сферического зеркала
то получим формулу сферического зеркала
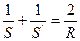 .
.
Величина 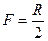 называется фокусным расстоянием зеркала. Если R>0, то
называется фокусным расстоянием зеркала. Если R>0, то 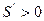 , т.е. изображение даваемое выпуклым зеркалом всегда мнимое.
, т.е. изображение даваемое выпуклым зеркалом всегда мнимое.
Если R>0, то 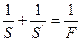 или,
или, 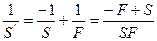 т.е.
т.е. 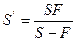 и в зависимости от значения S может быть как мнимое, так и действительным.
и в зависимости от значения S может быть как мнимое, так и действительным.
Если R→∞, то  и следовательно изображение даваемое плоским зеркалом всегда мнимое.
и следовательно изображение даваемое плоским зеркалом всегда мнимое.
Лучи света, от источника конечных размеров пройдя через сферические поверхности раздела, могут дать стигматическое изображение предмета.
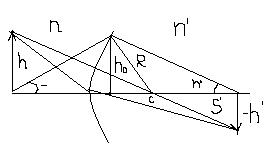
Линейное увлечение V есть отношение поперечного размера изображения 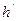 к поперечному размеру изображения h.
к поперечному размеру изображения h. 

Угловым увеличением W называется отношение значения угла  под которым лучи сходятся в точку изображения, к значению угла и под которым соответствующие лучи выходят от источника.
под которым лучи сходятся в точку изображения, к значению угла и под которым соответствующие лучи выходят от источника.
Из подобия треугольников:
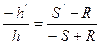 или
или 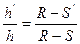 , но
, но 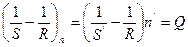 т.е.
т.е. 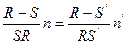 но
но 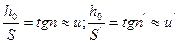 т.е.
т.е. 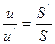 поэтому
поэтому 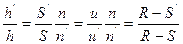 или nuh=
или nuh= 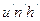 теорема Лагранжа- Гельмгольца т.е. произведение линейного увеличения
теорема Лагранжа- Гельмгольца т.е. произведение линейного увеличения  . Углового увеличения
. Углового увеличения 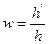 и отношение показателей преломления 2-х сред к
и отношение показателей преломления 2-х сред к 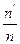 для сферической поверхности есть величина постоянная n=1:
для сферической поверхности есть величина постоянная n=1: 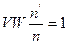

Зеркала, линзы призмы, оптические приборы
Зеркала
Простейшим оптическим устройством, способным создавать изображение предмета, является плоское зеркало. Изображение предмета, даваемое плоским зеркалом, формируется за счет лучей, отраженных от зеркальной поверхности. Это изображение является мнимым, так как оно образуется пересечением не самих отраженных лучей, а их продолжений в «зазеркалье» (рис 3.2.1).

|
| Рисунок 3.2.1. Ход лучей при отражении от плоского зеркала. Точка S' является мнимым изображением точки S |
Вследствие закона отражения света мнимое изображение предмета располагается симметрично относительно зеркальной поверхности. Размер изображения равен размеру самого предмета.
Сферическим зеркалом называют зеркально отражающую поверхность, имеющую форму сферического сегмента. Центр сферы, из которой вырезан сегмент, называют оптическим центром зеркала. Вершину сферического сегмента называют полюсом. Прямая, проходящая через оптический центр и полюс зеркала, называется главной оптической осью сферического зеркала. Главная оптическая ось выделена из всех других прямых, проходящих через оптический центр, только тем, что она является осью симметрии зеркала.
Сферические зеркала бывают вогнутыми и выпуклыми. Если на вогнутое сферическое зеркало падает пучок лучей, параллельный главной оптической оси, то после отражения от зеркала лучи пересекутся в точке, которая называется главным фокусом F зеркала. Расстояние от фокуса до полюса зеркала называют фокусным расстоянием и обозначают той же буквой F. У вогнутого сферического зеркала главный фокус действительный. Он расположен посередине между центром и полюсом зеркала (рис 3.2.2).
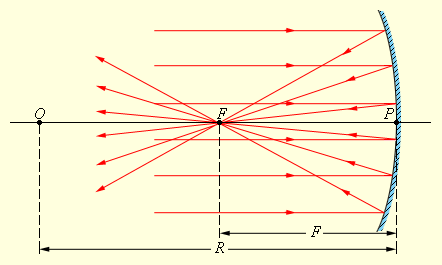
|
| Рисунок 3.2.2. Отражение параллельного пучка лучей от вогнутого сферического зеркала. Точки O – оптический центр, P – полюс, F – главный фокус зеркала; OP – главная оптическая ось, R – радиус кривизны зеркала |
Следует иметь в виду, что отраженные лучи пересекаются приблизительно в одной точке только в том случае, если падающий параллельный пучок был достаточно узким (так называемый параксиальный пучок).
Главный фокус выпуклого зеркала является мнимым. Если на выпуклое зеркало падает пучок лучей, параллельных главной оптической оси, то после отражения в фокусе пересекутся не сами лучи, а их продолжения (рис 3.2.3).
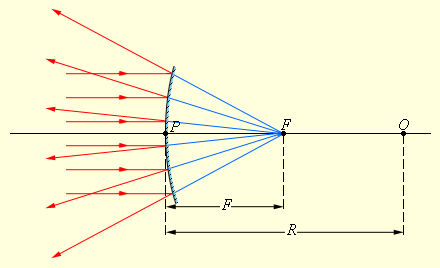
|
| Рисунок 3.2.3. Отражение параллельного пучка лучей от выпуклого зеркала. F – мнимый фокус зеркала, O – оптический центр; OP – главная оптическая ось |
Фокусным расстояниям сферических зеркал приписывается определенный знак: для вогнутого зеркала 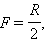 для выпуклого
для выпуклого 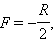 где R – радиус кривизны зеркала.
где R – радиус кривизны зеркала.
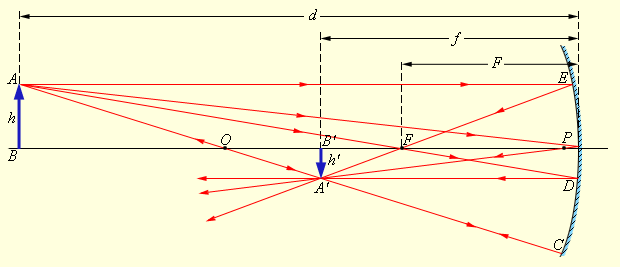
Изображение какой-либо точки A предмета в сферическом зеркале можно построить с помощью любой пары стандартных лучей:
- луч AOC, проходящий через оптический центр зеркала; отраженный луч COA идет по той же прямой;
- луч AFD, идущий через фокус зеркала; отраженный луч идет параллельно главной оптической оси;
- луч AP, падающий на зеркало в его полюсе; отраженный луч симметричен с падающим относительно главной оптической оси.
- луч AE, параллельный главной оптической оси; отраженный луч EFA 1 проходит через фокус зеркала.
На рис 3.2.4 перечисленные выше стандартные лучи изображены для случая вогнутого зеркала. Все эти лучи проходят через точку A', которая является изображением точки A. Все остальные отраженные лучи также проходят через точку A'. Ход лучей, при котором все лучи, вышедшие из одной точки, собираются в другой точке, называется стигматическим. Отрезок A'B' является изображением предмета AB. Аналогичны построения для случая выпуклого зеркала.
|
| Рисунок 3.2.4. Построение изображения в вогнутом сферическом зеркале |
Положение изображения и его размер можно также определить с помощью формулы сферического зеркала:
|
Здесь d – расстояние от предмета до зеркала, f – расстояние от зеркала до изображения. Величины d и f подчиняются определенному правилу знаков:
- d > 0 и f > 0 – для действительных предметов и изображений;
- d < 0 и f < 0 – для мнимых предметов и изображений.
Для случая, изображенного на рис 3.2.4, имеем:
F > 0 (зеркало вогнутое); d = 3 F > 0 (действительный предмет).
По формуле сферического зеркала получаем: 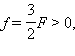 следовательно, изображение действительное.
следовательно, изображение действительное.
Если бы на месте вогнутого зеркала стояло выпуклое зеркало с тем же по модулю фокусным расстоянием, мы получили бы следующий результат:
F < 0, d = –3 F > 0, 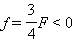 – изображение мнимое.
– изображение мнимое.
Линейное увеличение сферического зеркала Γ определяется как отношение линейных размеров изображения h ' и предмета h.
Величине h ' удобно приписывать определенный знак в зависимости от того, является изображение прямым (h' > 0) или перевернутым (h' < 0). Величина h всегда считается положительной. При таком определении линейное увеличение сферического зеркала выражается формулой, которую можно легко получить из рис 3.2.4:
|
| Построение изображения в выпуклом зеркале | ||
| Положение объекта | изображение | построение |
| любое | мнимое прямое уменьшенное | 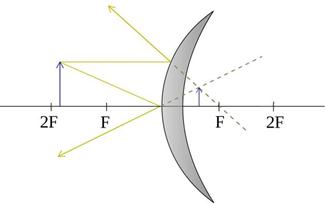
|
| Построение изображения в вогнутом зеркале | ||
| Положение объекта | изображение | построение |
| Между фокусом и зеркалом | мнимое прямое увеличенное | 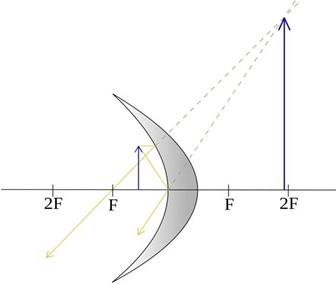
|
| Между фокусом и зеркалом | В бесконечности | 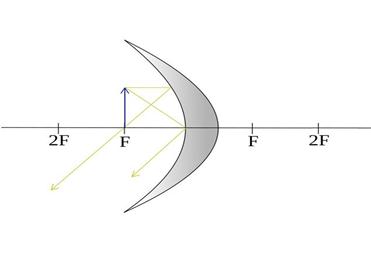
|
| Между фокусом и центром кривизны (2F) | Действительное Перевёрнутое Увеличенное | 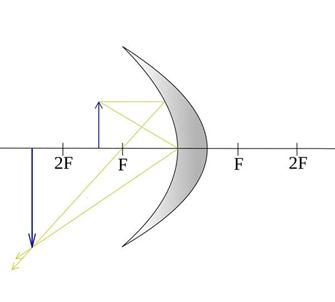
|
| В центре кривизны | Действительное Перевёрнутое Того же размера и На том же расстоянии | 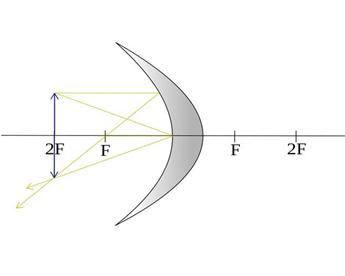
|
| На расстоянии, большем чем 2F | Действительное Перевёрнутое Уменьшенное | 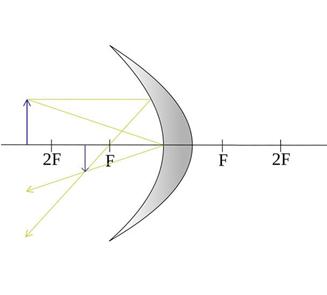
|
Призма
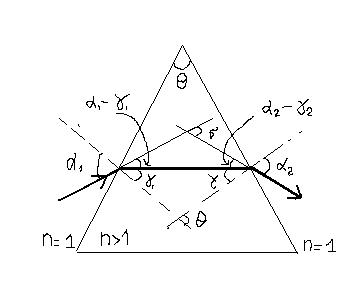
 - преломляющий угол
- преломляющий угол
б - угол отклонения луча;
так как б- внешний угол ∆, то 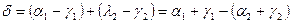
но 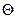 так же есть внешний угол другого ∆ и поэтому
так же есть внешний угол другого ∆ и поэтому  , т.е.
, т.е. 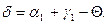 так как
так как 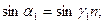
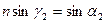 , то Исследуем на экстремум функцию угла отклонения луча. Беря производную от б по γ, и приравняв к нулю:
, то Исследуем на экстремум функцию угла отклонения луча. Беря производную от б по γ, и приравняв к нулю: 
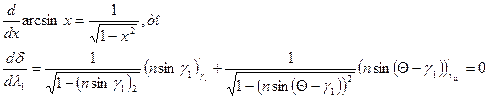
Или
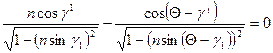 . Если
. Если  , то это удовлетворяется; а так как
, то это удовлетворяется; а так как 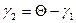 , то
, то 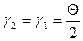
 , т.е. ход лучей должен быть симметричным. При этом получается min угол отклонения, так как при
, т.е. ход лучей должен быть симметричным. При этом получается min угол отклонения, так как при  и
и 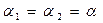 , т.е.
, т.е. 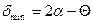 . Отсюда
. Отсюда 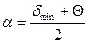 , а так как
, а так как 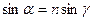 , то
, то 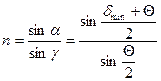
Это уравнение применяется для определения n по углу минимального отклонения.
Опыт показывает, что стеклянные призмы сильнее преломляют коротковолновую часть спектра (синие лучи), и что нет линейной связи между 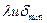 . Мера дисперсии
. Мера дисперсии 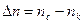 (с- синий, к- красный).
(с- синий, к- красный).
Date: 2015-05-08; view: 4032; Нарушение авторских прав