Принцип Ферма. Законы отражения и преломления

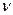В предельном случае перехода к геометрической оптике (λ→0) распространения волнового фронта может быть найдено простым построением. В каждой точке волнового фронта построим сферу с радиусом ,где - скорость волны, 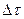-б/м промежуток времени. Поверхность 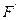огибающая эти сферы также есть поверхность равной фазы, так как все точки её будут иметь к моменту 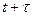те же фазы, что и точки поверхности F к моменту t. Отрезки прямых dn соединяющие точки фронта F

С точкой касания соответствующей сферы и огибающей, представляют собой элементы луча, перпендикулярные к поверхности фронта.

Продолжая построения можно шаг за шагом определить поверхность равной фазы и в то же время найти направление лучей (из отрезков dn). Таким образом, действительный путь распространения света (луч) есть путь, для нахождения которого свету требуется min время по сравнению с любым другим мыслимым путем между теми же точками.

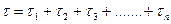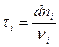Действительно от А до В вдоль луча свет проходит за время , где т.е.

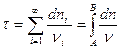
Всякий другой путь больше и 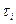отличается, больше, чем при распространении по нормам. Таким образом, действительно путь распространения света (луч) соответствует min времени распространения (принцип Френеля).

Эта теорема в геометрической оптике представляет аксиому, сформулированную Ферма (1660г.) как общий закон распространения света.

Для однородной среды этот принцип приводит к закону прямолинейного распространения согласно геометрической аксиоме о том, что прямая есть кратчайшее расстояние между двумя точками.

Для случая перехода через границу различных сред этот принцип дает законы отражения и преломления света. Любой путь 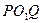лежащей вне плоскости падения проходиться светом за большее время, чем путь POQ проведенный в плоскости падения. И в согласии с принципом Ферма путь, требующий минимального времени должен лежать в плоскости падения (т.е плоскости перпендикулярна к границе раздела и проходящая через P и Q).

Таким образом, получим первый закон преломления.

Чтобы из всех путей от Р до Q лежащих в плоскости падения выбрать путь, требующий min времени, исследуем как меняется это время в зависимости от положения точки О.

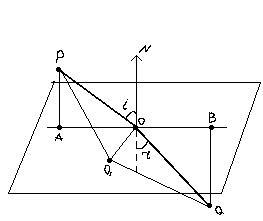
Путь АО=х; РА= 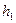; QB= 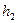; AB=P; OB=P-x.

Время распространения света по пути POQ будет:

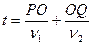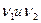, где скорости света в этих средах.

Или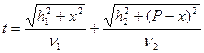

Условие min времени есть 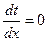т.е.

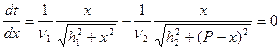
или

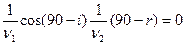
т.е. или 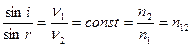относительный показатель преломления среды 2 относительно среды 1.

Абсолютный показатель .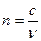

Для малых углов закон преломления .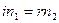

При формальной замене 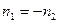получаем закон отражения 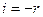. Таким образом, любую формулу, выведенную для преломляющих систем можно использовать для описания явлений в отражающих системах.

Понятие: Если пучок лучей имеет одну общую вершину, то его называют гомоцентрическим.

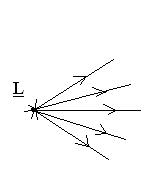
Если после отражения и преломления это пучок превращается в пучок, сходящийся также в точку, то гомоцентричность сохраняется и эта точка 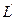сопряжена с L, или является изображением точки L.

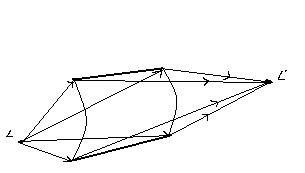Систему,сохраняющую гомоцентричность пучка называют стигматической. В противном случае – астигматической.

Так как в практической оптике обычно ставиться задача получения изображений, точно передающих форму источника, то важнейшим вопросом лучевой оптики является выяснение условий сохранения гомоцентричности пучков.

Date: 2015-05-08; view: 821; Нарушение авторских прав