Туннельный эффект. При описании твёрдого тела на основе квантовой механики возникает ряд эффектов, которые никаким образом нельзя объяснить исходя из классических представлений

При описании твёрдого тела на основе квантовой механики возникает ряд эффектов, которые никаким образом нельзя объяснить исходя из классических представлений физики твёрдого тела. Одним из таких эффектов является – туннельный эффект.

Туннельный эффект – эффект прохождения частицы через потенциальный барьер (с энергией U) даже если полная энергия частицы E меньше U.

Для описания туннельного эффекта используется уравнение Шрёдингера в стационарной форме. Это уравнение имеет вид:

,

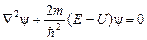где 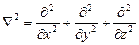– оператор Лапласа; y (x, y, z) – пси-функция; m – масса частицы; – постоянная Планка с чертой.

Физический смысл имеет квадрат пси-функции. Квадрат модуля пси-функции |y (x, y, z)|² – определяет вероятность того, что частица будет обнаружена вблизи данной точки с координатами x, y, z в пределах объёма dV.

Пусть частица, движущаяся слева направо с энергией E, встречает на своём пути потенциальный барьер с потенциальной энергией U ₀ (высота) ширины l (рис. 1).

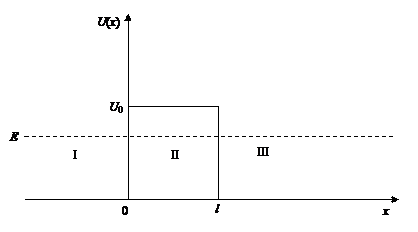
Рис. 1

Исходя из уравнений Шрёдингера, получается, что для любой энергии E имеется вероятность того, что частица отразится от барьера и полетит в обратную сторону (даже если Е > U ₀). Кроме того, имеется ненулевая вероятность, что частица пройдёт «сквозь» барьер и окажется в области III (даже при E < U ₀). Такое невозможно по законам классической механики.

Рассмотрим случай E < U ₀. В этом случае уравнение Шрёдингера имеет вид:

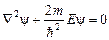, (1)

для областей I и III и

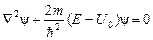, (2)

для области II, причём E – U ₀ < 0.

Решение уравнений (1) и (2) имеет вид:

;

;

,

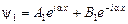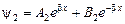где y₁, y₂, y₃– пси-функции соответственно для I, II и III областей; 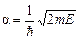; 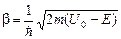. Причём 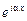– соответствует волне распространяющейся в положительном направлении, а – волне распространяющейся в отрицательном направлении.

В области III имеется только волна, прошедшая сквозь барьер и распространяющаяся только в положительном направлении. Следовательно, B ₃ равно 0. Для нахождения неизвестных параметров A ₁, B ₁, A ₂, B ₂ и A ₃ используем тот факт, что y-функция и её производная должны быть на границе непрерывны, т.е. y₁(0) = y₂(0), y₂(l) = y₃(l), y₁’(0) = y₂’(0) и y₂’(l) = y₃’(l). Мы получили четыре уравнения с пятью неизвестными, что не позволяет нам определить все неизвестные величины. Однако из этих соотношений можно определить коэффициент отражения 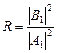и коэффициент прохождения (прозрачности) 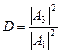. Решая полученные соотношения для коэффициента прохождения, получим соотношение:

.

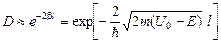В случае потенциального барьера произвольной формы, как показано на рис. 2, для коэффициента прохождения получается соотношение:

.

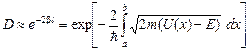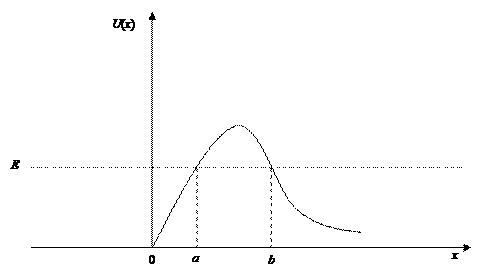
Рис. 2

Date: 2015-05-08; view: 567; Нарушение авторских прав