Зоны Шустера и спираль Корню

Рис. 3

В одномерных задачах дифракции, например на прямолинейной щели, целесообразно разбивать волновой фронт на полосатые зоны. В случае, когда волновой фронт плоский (обобщение на случай сферического фронта не встречает никаких затруднений) и плоскость волнового фронта АВ перпендикулярна к плоскости Рис. 3, опустим перпендикуляр OP из точки наблюдения P на волновой фронт. Обозначим через b длину этого перпендикуляра. Проведем цилиндрические коаксиальные поверхности, ось которых проходит через точку Р перпендикулярно к плоскости рисунка, а радиусы равны b, b+l/2, b+l,... Тогда волновой фронт разобьется на прямоугольные полосы, которые называются зонами Шустера. Центральную зону условимся считать за две зоны: одна расположена справа, а другая слева от точки О. Тогда:

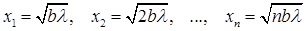(4).

Ширины последовательных зон Шустера будут

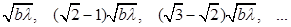(5).

Они монотонно убывают и в пределе, когда rà¥, стремятся к l/2, как это ясно из их построения. (Впрочем, высшие зоны не играют роли. Имеют значение только несколько десятков первых зон Шустера.)

Как и в случае зон Френеля, применим графический метод (Рис. 2). Каждую зону Шустера разобьем на узкие полоски и будем изображать колебание в точке Р, вносимое отдельной полос­кой, вектором на векторной диаграмме. Затем перейдем к пределу, устремляя к нулю ширину каждой полоски. В результате получится плавная кривая, называемая спиралью Корню (1841—1902) (рис. 4). Она состоит из двух симметричных ветвей, бесконеч­ное число раз обвивающихся во­круг фокусов F и F’ и неогра­ниченно приближающихся к ним.

Верхняя ветвь представляет действие правой половины волнового фронта, нижняя — левой. Отличие каждой из ветвей от соответствующей спирали на Рис. 2 обусловлено более быстрым убыванием начальных зон Шустера, чем зон Френеля. Колебание, возбуждаемое первой правой зоной Шустера, изображается вектором 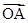, второй правой вектором 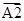, двумя первыми правыми зонами вместе — вектором 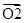и т. д. (все эти векторы на рис. 4 не 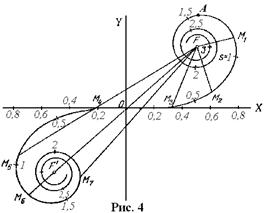проведены). Колебание, возбуждаемое всем волновым фронтом, представляется вектором 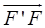, соединяющим фокусы спирали Корню. По мере приближения к фокусам ампли­туды колебаний становятся все меньше и меньше и в пределе обра­щаются в нуль.

Положение точки на спирали Корню определяется значением параметра 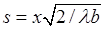(значения указаны на спирали на Рис. 4), где x – расстояние от точки наблю­дения Р до центра картины, b – расстояние от точки наблюдения до экрана.

Date: 2015-05-08; view: 2380; Нарушение авторских прав