Дифракция на краю полуплоскости

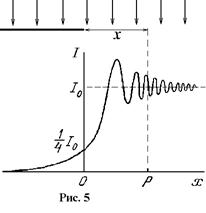
Рассмотрим в качестве примера дифракционную картину от прямолинейного края экрана (рис. 5). Где бы ни находилась точка наблюдения P, для нее всегда будет открыт правый край волнового фронта. На векторной диаграмме (рис. 4) колебание в точке на­блюдения представится вектором 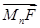, конечная точка которого всегда находится в верх­нем фокусе F, а начальная M_n лежит где-то на спирали Корню.

Если, сохраняя неизменным положение конеч­ной точки F, перемещать на­чальную точку M_n вдоль спи­рали Корню (положения М₁, М₂, M₃,,…), то таким путем можно получить распределение ампли­туд и интенсивности колебаний света по всему экрану.

С деталями анализа дифракции на краю полуплоскости можно познакомиться по учебникам, список которых приведен в конце сборника. Здесь же приведены результаты этого анализа.

Распределение интенсивности графически представлено на рис. 5. Как видим, нет резкой границы между светом и тенью: в области геометрической тени интенсивность света убывает непрерывно и монотонно, а освещенная область расщепляется в дифракционные полосы.

На рис. 6 а) показана дифракционная картина, наблюдаемая при дифракции света на крае экрана. Таким же путем можно рассчитать дифракционную картину на щели или длинном прямоугольном экране. На рис. 6 б) показана тень проволоки от точечного (или линейного) источника.

Date: 2015-05-08; view: 1384; Нарушение авторских прав