
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Геометрическая оптика и дифракция
|
|
Законы геометрической оптики достаточно точны, если длину световой волны l можно считать бесконечно малой величиной. Чем хуже выполнено это условие, тем сильнее проявляются отклонения от законов геометрической оптики, приводящие к возникновению явлений дифракции. По законам геометрической оптики за краем непрозрачного экрана должна находиться область тени (геометрическая тень), резко ограниченная от освещенных областей и соответствующая профилю края экрана. Вследствие дифракции вместо этого получается сложное распределение интенсивности, называемое дифракционной картиной.
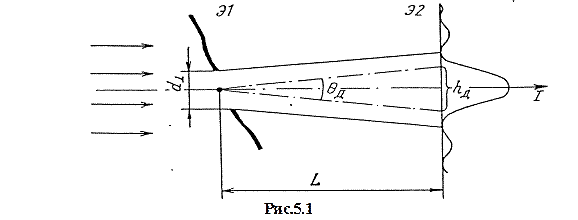
УГОЛ ДИФРАКЦИИ
Пусть отверстие в экране Э1 «вырезает» пучок из плоской монохроматической волны (рис.5.1), и след пучка наблюдается на экране Э2. Уменьшая размер отверстия, заметим, что вначале размер следа пучка уменьшается в соответствии с размером отверстия, но затем начинает увеличиваться: пучок становится расходящимся. Угловая ширина пучка (угол дифракции qд) определяется соотношением между длиной волны l и характерным размером пучка d в плоскости, перпендикулярной направлению распространения волны:
qд ~ l/ d (5.1)
Соотношение (5.1) позволяет оценить порядки дифракционных эффектов. Смысл его в том, что любое пространственное ограничение волны вызывает её расхождение в соответствии с (5.1). Если вместо экрана Э1 с отверстием в пучок излучения вносится препятствие размером d, то расходящийся дифракционный пучок наблюдается на фоне незакрытого «прямого» пучка.
ДЛИНА ДИФРАКЦИИ
Вследствие дифракционной расходимости размер освещенной области на экране Э2 будет превышать начальные размеры пучка d. Дополнительное дифракционное уширение
h д = L qд (5.2)
Если h д < df, то размер пятна практически равен d, а распределение интенсивности определяется законами геометрической оптики.
Расстояние qд, на котором дифракционное уширение становится сравнимым с начальным размером пучка, называют длиной дифракции. Из условия L дqд ~ d находим:
L д ~ d 2 / l (5.3)
Если выполняется записанное в различных формах условие
L < L д; l < d 2/ L; d > 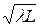 , (5.4)
, (5.4)
то «работает» геометрическая оптика. Если же
L ³ L д; l ³ d 2/ L; d ³ 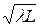 , (5.5)
, (5.5)
то существенно явление дифракции. При L > L д размер пятна h д > d, и распределение интенсивности полностью определяется дифракцией.
Характер распределения интенсивности в дифракционной картине зависит от отношения длины дифракции L д к расстоянию от экрана L до плоскости наблюдения, т.е. от безразмерного параметра дифракции.
m = L д/ L = d 2 /l L (5.6)
ДИФРАКЦИЯ ФРЕНЕЛЯ И ДИФРАКЦИЯ ФРАУНГОФЕРА
Если L ~ L д имеем наиболее сложный для анализа вид дифракции, называемый дифракцией Френеля. Если L > L д, то распределение интенсивности на экране Э2 и его расчет упрощаются. Лучи, идущие от экрана Э1 в произвольную точку Р экрана Э2, почти параллельны, а приходящие в точку Р волны - плоские. Такой вид дифракции называют дифракцией Фраунгофера (дифракция в параллельных лучах или дифракция плоских волн).
Область за экраном Э1 можно разбить на три участка:
1) L < L д; m > 1 - область геометрической оптики;
2) L ~ L д; m ~ 1 - дифракция Френеля (ближняя зона дифракции);
3) L > L д; m £ 1 - дифракция Фраунгофера (дальняя зона дифракции).
ДИФРАКЦИЯ НА ЩЕЛИ И НА НИТИ
Если отверстие в экране Э1 имеет вид длинной щели шириной d, то уширение пучка происходит только в направлении, перпендикулярном щели. Вдоль щели пучок не ограничен и дифракционного уширения практически нет.
Дифракционная картина Фраунгофера состоит из центрального максимума и побочных минимумов меньшей интенсивности (рис.5.2).
В качестве характерного размера картины возьмем ширину побочных максимумов, определяемую как расстояние между соседними минимумами. Центральный максимум вдвое шире. Соотношение (5.1) для щели оказывается точным, и из него следует
D х = l L / d, (5.7)
и координаты минимумов х m = m l L / d, где m = ±1, ±2, ±3,…..
Точно так же выглядит дифракционная картина от препятствия в виде стержня, нити или волоса толщиной d, но эта картина наблюдается на фоне незакрытого пучка исходного излучения, и исследовать ее можно лишь за пределами этого пучка.
Дифракционная картина Френеля является более сложной, при этом в центре картины может быть как максимум, так и минимум интенсивности.
Date: 2015-05-08; view: 770; Нарушение авторских прав