Геометрическая оптика. Законы отражения и преломления света (рис. 2. 1):

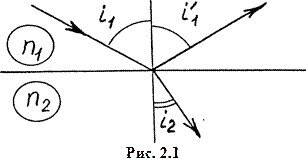
Законы отражения и преломления света (рис.2.1):

i ₁ = i ^/₁, (2.1)

n ₁ sin i ₁ = n ₂ sin i ₂. (2.2)

При малых углах падения (i ₁ << 1):

n ₁ i ₁» n ₂ i ₂ . (2.3)

Пучок параллельных лучей после прохождения через линзу становится сходящимся или расходящимся (рис.2.2 а, б). Точка пересечения лучей пучка, прошедшего через собирающую линзу (рис.2.2 а), или продолжений лучей для рассеивающей линзы (рис.2.2 б) лежит в фокальной плоскости линзы. Эту точку можно рассматривать как точечный источник света.

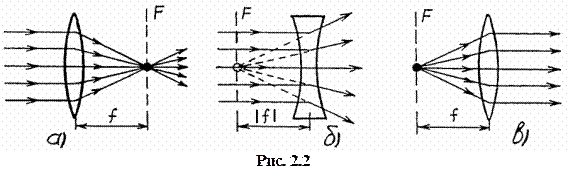
Волна, выходящая из точки в фокальной плоскости собирающей линзы, после линзы становится плоской (пучок параллельных лучей на рис.2.2 в) по этому признаку можно определить фокусное расстояние собирающей линзы.

На практике, при конструировании и проектировании различных оптических приборов (систем), например, таких как микроскопы, бинокли, зрительные трубы, телескопы и ряд других, часто возникает необходимость проводить геометрическое построение хода лучей, источниками которых могут являться различные объекты. При этом, если оптическая система содержит значительное число линз, то построение изображение производится поэтапно: сначала ход лучей от объекта, являющегося первоисточником света, рассматривают только в одной, самой первой линзе по ходу лучей, получая первое изображение от нее, затем даваемое ею изображение (действительное или мнимое) рассматривают как источник для второй линзы, рассматривая ход лучей через вторую линзу и получают второе изображение и затем повторяют процесс до тех пор, пока не получат окончательное изображение, даваемое последней линзой в оптической системе.

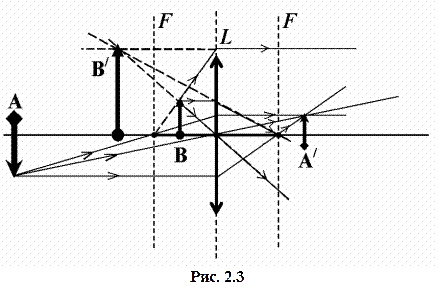
При построении хода лучей через собирающую линзу L (см. рис. 2.3) используют наиболее «удобные» лучи. Так, например, если объект находится перед собирающей линзой, то такими удобными лучами могут быть любые два луча из трех следующих:

1- луч, идущий от объекта через оптический центр линзы (он не преломляется);

2- луч, идущий параллельно главной оптической оси линзы (преломившись, он пройдет через второй фокус линзы);

3- луч или его продолжение (для объекта В на рис. 2.3), прошедший перед линзой через ее первый фокус (такой луч после преломления пойдет параллельно главной оптической оси).

Изображение какой-либо точки объекта получается на пересечении любых двух лучей из 3-х указанных (если объект находится перед фокусом) или на продолжении преломленных лучей (если объект находится между плоскостью линзы и ее фокальной плоскостью).

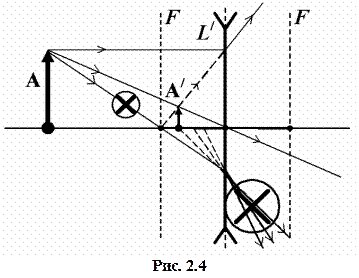При построении хода лучей через рассеивающую линзу L^/ (рис. 2.4) такими удобными лучами могут быть только два луча:

1- луч, идущий от объекта через оптический центр линзы;

2- луч, идущий параллельно главной оптической оси линзы (его продолжение пройдет через первый фокус линзы).

Луч, прошедший перед линзой через ее фокус, не является удобным, поскольку его продолжение пересекает оптическую ось линзы между фокусом и плоскостью линзы и при схематическом построении хода лучей сложно определить «на глаз» точное место такого пересечения.

Формула тонкой линзы (рис.2.5)

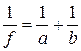, (2.3)

где f - фокусное расстояние линзы. Для рассеивающей линзы расстояния f и b надо считать отрицательными. Для собирающей линзы, дающей мнимое изображение (объект находится между фокусом и плоскостью линзы) b нужно считать отрицательным.

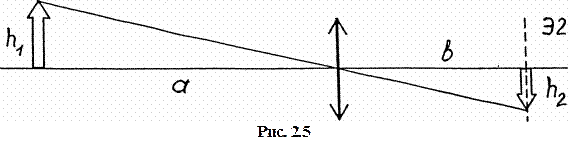
Поперечное увеличение линзы (рис.2.5)

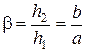. (2.4)

Отсюда следуют методы измерения размера предмета или расстояния h ₁ между двумя точками.

Первый метод: измерив a, b и h ₂, находим

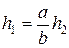. (2.5)

Второй метод. Получив изображение величиной h ₂ на расстоянии b от линзы, перемещаем ее до тех пор, пока в той же точке (на расстоянии l = a + b от предмета) не получится еще одно его изображение величиной 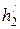. Очевидно, что при этом новое расстояние a станет равным старому расстоянию b, и наоборот. Из (2.3) и (2.4) следует

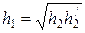. (2.6)

Третий метод. В отличие от предыдущего случая будем перемещать как линзу, так и экран Э2 (рис.2.5), в плоскости которого наблюдаем изображение. Если размер первоначального изображения был h ₂, а после перемещения линзы на расстояние d стал 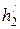(в новой плоскости экрана Э2), то из (2.3) и (2.5) получаем:

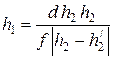. (2.7)

Второй и третий методы пригодны как для тонкой линзы, так и для толстой линзы. Кроме того, они не требуют знания положения линзы. В третьем методе достаточно знать лишь ее перемещение.