Теория идеальной оптической системы

Рассмотрим оптическую систему, состоящую из ряда сферических поверхностей, разделяющих среды с различными показателями преломления (например, набора линз). Пусть центры кривизны поверхностей лежат на одной прямой – оптической оси системы. Такие системы называют центрированными. Оптическая ось является осью симметрии.

Назовем пространством предметов ту область трехмерного пространства, в которой располагаются изображаемые оптической системой предметы. Область пространства, в которой возникают оптические изображения этих предметов, назовем пространством изображений. В общем случае оба пространства могут перекрываться.

Оптическая система называется идеальной, если каждой точке, прямой и плоскости из пространства предметов однозначно соответствуют сопряженные с ними (т.е. являющиеся их изображениями) точка, прямая и плоскость в пространстве изображений. Отсюда следует, что гомоцентрическому пучку в пространстве предметов соответствует сопряженный с ним гомоцентрический пучок в пространстве изображений. Плоскость, проходящая через оптическую ось, называется меридиональной. Меридиональной плоскости в пространстве предметов соответствует сопряженная с ней меридиональная плоскость в пространстве изображений. Из соображений симметрии следует, что плоскости, перпендикулярной оптической оси в пространстве предметов, соответствует сопряженная плоскость в пространстве изображений, также перпендикулярная оптической оси. Геометрическая оптика 2-18

Заметим, что реальная оптическая система обладает перечисленными свойствами идеальной, если изображения создаются параксиальными лучами, т.е. лучами, распространяющимися вблизи оптической оси и составляющими малый угол с оптической осью. При этих условиях излагаемая ниже теория целиком приложима для описания работы реальных оптических систем.

Изобразим условно оптическую систему, указав первую 1 и последнюю 2 преломляющие поверхности (рис.2), и будем для конкретности считать, что пространство предметов расположено слева от системы, а пространство изображений – справа.

Фокусы системы. Введем понятие фокусов системы. Направим луч 1 в пространстве предметов параллельно оптической оси и будем считать, что сопряженный луч 1’ пересекает оптическую ось в пространстве изображений в точке F’ (рис.2). Сопряженная с точкой F’ точка в пространстве предметов находится на пересечении сопряженных прямых (луч 1 и оптическая ось) и лежит на бесконечности. Очевидно, что в F’ пересекаются все лучи, параллельные оптической оси в пространстве предметов.

Точка F’, являющаяся изображением бесконечно удаленной точки на оптической оси, называется задним фокусом системы.

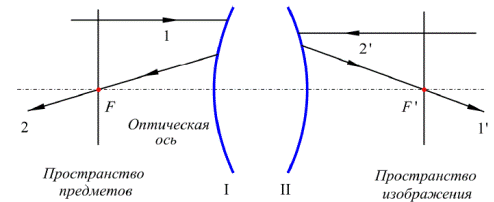
Рис.2. Фокусы и фокальные плоскости оптической системы

Направим некоторый луч 2’ в пространстве изображений параллельно оптической оси и будем считать, что сопряженный луч 2 пересекает ось в пространстве предметов в точке F. Изображение точки F лежит на оптической оси в пространстве изображений и находится на бесконечности. Точка F называется передним фокусом системы. Плоскости, проходящие через точки F и F’, перпендикулярные оптической оси, называются, соответственно, передней и задней фокальными плоскостями.

Главные плоскости. Введем понятие главных плоскостей системы. Направим луч 1 параллельно оптической оси на высоте h от нее (рис.3). Сопряженный луч 1’, по определению пройдет через задний фокус системы F’. Случай, когда луч 1 также параллелен оптической оси системы, относится к особому классу телескопических систем, которые в настоящей работе не рассматриваются. Проведем через передний фокус F луч 2 с таким расчетом, чтобы сопряженный луч 2’, параллельный оптической оси, также находился на высоте h. Продолжим луч 2 до пересечения с лучом 1 в точке R, а луч 1’ с лучом 2’ в точке R’. Точки R и R’, лежащие на пересечении сопряженных лучей, также являются сопряженными. Большая оптическая скамья 2-19

Проведем через них плоскости, перпендикулярные оси и пересекающие ее в точках H и H’ (сами плоскости принято обозначать теми же буквами).

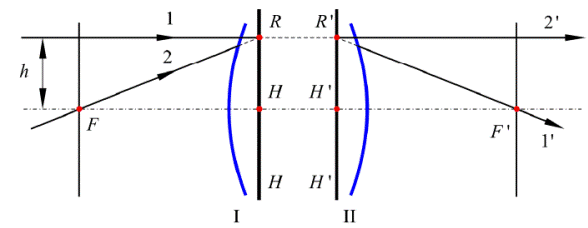
Рис.3. Главные плоскости и кардинатные точки оптической системы

Отрезок R’H’ является изображением отрезка RH. По построению RH=R’H’. Сопряженные плоскости H и H’, для которых линейное увеличение ''1RHRHβ==, называются главными плоскостями. Плоскость H, принадлежащая пространству предметов, называется передней главной плоскостью, плоскость H’, принадлежащая пространству изображений – задней главной плоскостью. Любой луч в пространстве предметов, пересекающий плоскость H на высоте h, входит в пространство изображений, пересекая H’ на той же высоте. Это свойство главных плоскостей существенно упрощает определение хода лучей через оптическую систему.

Точки F, F’, H и H’ называются кардинальными точками оптической системы.

Приведенное на рис.3 расположение кардинальных точек относительно преломляющих поверхностей приблизительно соответствует случаю симметричной двояковыпуклой линзы. Для линз другой формы и для сложных оптических систем это расположение может быть другим и, в частности, плоскости H и H’ могут находиться вне оптической системы.

При расчете оптических систем взаимное расположение элементов системы, включая положение предмета и его изображения, задается путем указания их координат вдоль оптической оси. Эти координаты отсчитываются от заранее оговоренного начала отсчета и могут выражаться как положительными, так и отрицательными числами. В геометрической оптике обычно принимают, что свет распространяется слева направо, и это направление считается положительным. Величина предмета l или его изображения l’ в меридиональной плоскости задается координатой крайней точки, отсчитываемой от оптической оси в перпендикулярном направлении. Положительным считается направление вверх.

Начала отсчета координат и принятые для них обозначения приведены на рис.4. Направления отсчета указаны стрелками на размерных линиях. Как это принято в геометрической оптике, буквенные обозначения отрицательных координат указаны на чертеже со знаком минус. Благодаря этому отрицательные координаты описываются положительными величинами, которые могут быть использованы в геометрических соотношениях, считываемых с чертежа.

Координаты предмета на оптической оси отсчитываются от передней главной плоскости H или от переднего фокуса F. Координаты изображения, соответственно, отсчитываются от точек H’ и F’. Геометрическая оптика 2-20

Координаты фокусов отсчитываются относительно соответствующих главных плоскостей.

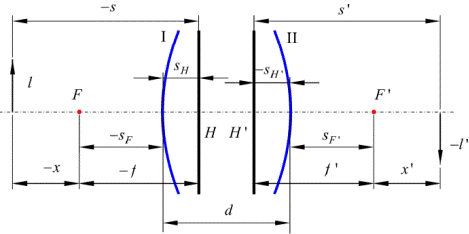
Рис.4. Координаты основных точек в оптической системе и принятые для них обозначения

Положение кардинальных точек H и F в реальной оптической системе определяется относительно первой (по ходу луча) преломляющей поверхности 1, положение кардинальных точек H’ и F’- относительно последней поверхности 2.

Очевидно, что расположение кардинальных точек относительно преломляющих поверхностей не зависит от того, с какой стороны системы расположен источник. При повороте системы на 180° относительно направления, перпендикулярного оптической оси, кардинальные точки H, F и H’, F’, меняются ролями.

Заметим, что в литературе по геометрической оптике координаты элементов вдоль оптической оси называют «отрезками» или «расстояниями», которым приписываются определенные знаки. В частности, величины f и f’ называются, соответственно, передним и задним фокусными расстояниями. Они играют основную роль при описании работы оптических систем.

Величины sF и sF’ называются, соответственно, передним и задним фокальными отрезками. С их помощью оценивается расположение предмета и изображения относительно крайних преломляющих поверхностей системы.

Применение изложенной выше теории к описанию работы реальных оптических систем показывает, что соотношение между фокусными расстояниями в конкретной оптической системе определяется отношением показателей преломления сред, расположенных по обе стороны системы:

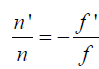
В частности, для преломляющей оптической системы в воздухе (n=n’=1) имеем f=-f'. Фокусные расстояния в этом случае одинаковы по величине, но имеют разные знаки, т.е. отсчитываются в разные стороны от соответствующих главных плоскостей. Оптические системы, для которых f’>0, называют положительными. Примером положительной оптической системы является собирающая линза в воздухе, а также сложные многолинзовые объективы различных приборов, в которых создаются действительные изображения.

Оптические системы, у которых f’<0, называются отрицательными. Примером отрицательной системы является рассеивающая линза.

Выведем некоторые соотношения, описывающие действие оптической системы и необходимые при выполнении экспериментальной части работы. Рассмотрим положительную оптическую систему (рис.5), заданную главными плоскостями и фокусами.

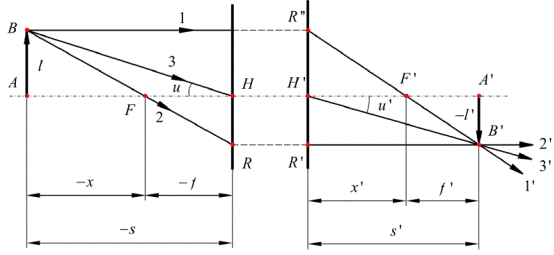
Рис.5. Построение изображения в оптической системе, заданной ее кардинальными точками

Пусть предмет, ограниченный точками А и В, имеет длину l и расположен на расстоянии s от передней главной плоскости. Выберем из всех лучей, выходящих из точки В, луч 1, параллельный оптической оси, и луч 2, направленный на передний фокус F. Сопряженный с лучом 1 луч 1‘ пересечет плоскость H’ на высоте l и пройдет через задний фокус F’. Луч 2’, сопряженный с лучом 2, пересечет плоскость H’ на высоте –l’ и далее пойдет параллельно оптической оси. Точка B’ пересечения лучей 1’ и 2’ будет изображением точки В. В эту точку соберутся все лучи, выходящие из точки В и попадающие в оптическую систему (в том числе луч 3, о роли которого см. ниже). Точку А’, являющуюся изображением точки А, найдем, опустив перпендикуляр из B’ на оптическую ось.

Из подобия треугольников ΔABF и ΔFHR, ΔA’B’F’ и ΔF’H’R” (рис.5) имеем

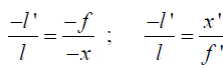
Заметим, что формулы (1) непосредственно определяют линейное увеличение β=l/l’. Сопоставляя оба равенства, получим формулу Ньютона

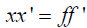(2)

Подставляя в формулу (2) значения 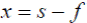и 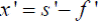, вытекающие непосредственно из чертежа, получим формулу Гаусса

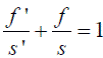(3)

Формулы Ньютона и Гаусса позволяют определить положение изображения при заданном положении предмета.

Прибавляя к обеим частям (2) величину xf’, получим

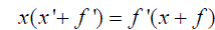
или (см. рис.5)

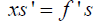(4)

Сопоставляя выражения (1) и (4), найдем еще одно выражение для линейного увеличения:

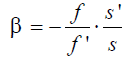(5)

Формулы (1), (2), (3) и (5) достаточно полно описывают действие оптической системы.

Сопоставим далее углы u и u’, образуемые сопряженными лучами 3 и 3’ с оптической осью. Из рис.5 имеем

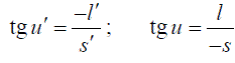(6)

Отсюда следует, что для оптической системы в воздухе 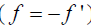углы u и u’ равны. Благодаря этому лучи 3 и 3’ также оказываются удобными для построения изображения.

Используем полученный результат для вывода соотношения, применяемого в экспериментальной части работы. Пусть малый объект высоты l находится в передней фокальной плоскости системы 1 (рис.6). В этом случае x1=0 и, как это следует из (2), изображение будет находиться на бесконечности. Изображение точки В создается параллельным пучком, составляющим с оптической осью угол

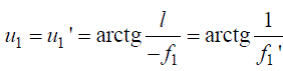(7)

Изображение точки А создается пуком лучей, параллельных оптической оси. Поэтому (7) определяет также угловую величину объекта и одновременно его изображения. Система 1 представляет собой так называемый коллиматор – оптическое устройство, предназначенное для получения параллельных пучков лучей.

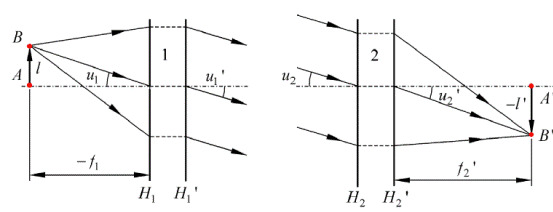
Рис.6. Формирование изображения в задней дипольной плоскости оптической системы (2) при расположении предмета AB в передней фокальной плоскости коллиматора (1)

Пусть далее параллельные пучки, выходящие из коллиматора, падают на систему 2, также находящуюся в воздухе. Для системы 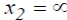и, следовательно, . Изображение l’ возникает в задней фокальной плоскости системы 2, причем:

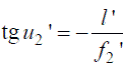(8)

Так как 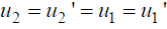то

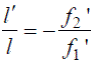(9)

Формулу (9) используют при определении фокусного расстояния и при оценке разрешающей способности исследуемой оптической системы, роль которой выполняет система 2.

Date: 2015-05-08; view: 2076; Нарушение авторских прав