Разрешающая способность линзы

Если освещающий свет идет от объекта к линзе, то он попадет в линзу, только если находится в пределах удвоенного угла , называемого апертурой линзы (Рис.4).

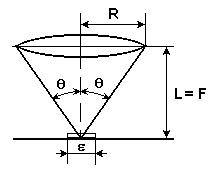
Рис.4. К определению разрешающей способности линзы

В этом случае разрешающая способность линзы , то есть минимальные размеры изображения, которое еще можно отделить от других, определяется выражением

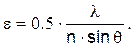
Здесь

n — показатель преломления среды, в которой находится линза;

 — апертура линзы;

 — длина волны.

Для когерентного света это означает, что в пределах апертуры должен находиться хотя бы первый порядок дифракции. Если в апертуру линзы попадают и лучи, соответствующие дифракционным максимумам более высоких порядков, то качество получаемого изображения повышается. Но условие попадания первого дифракционного максимума является обязательным.

Произведение A = n ·sin называется числовой апертурой линзы.

Учитывая, что линза располагается в воздухе (n = 1) и на фокусном расстоянии от объекта, из (4) с учетом рис.4 для числовой апертуры получаем

(5)

Здесь R — радиус линзы, а F — ее фокусное расстояние.

Тогда формулу (4) можно записать в виде

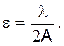
(6)

Поскольку линейные размеры пикселя на оптическом диске должны быть не меньше разрешающей способности линзы , определяемой формулой (6), то появляется возможность оценки минимально допустимого размера (радиуса) линзы, способной работать в считывающем устройстве CD ROM.

Эта же формула определяет и минимальный диаметр пятна, в который может быть сфокусирован свет линзой.

Date: 2015-05-08; view: 2117; Нарушение авторских прав