Экзаменационные билеты. Экзаменационные билеты содержат два теоретических вопроса и две задачи: первый вопрос и первая задача из раздела теории вероятностей

Экзаменационные билеты содержат два теоретических вопроса и две задачи: первый вопрос и первая задача из раздела теории вероятностей, второй вопрос и вторая задача из раздела математической статистики. Примеры экзаменационных билетов приведены ниже.

БИЛЕТ № 1

1. Предмет теории вероятностей. Испытанные события и их классификация.

2. Статистические гипотезы и их виды, нулевая и альтернативная гипотезы. Ошибки первого и второго рода. Уровень значимости.

3. Задачи.

Вновь созданная фирма набирает штат сотрудников. Из 7 претендентов все имеют равные шансы. Сколько всевозможных групп можно составить, если фирме требуется 3 работника на одинаковые должности?

Менеджер продуктового магазина желает оценить среднюю сумму, которую тратит покупатель на покупку молочных продуктов. Из предыдущего опыта он оценивает среднеквадратическое отклонение в 4 у.е. Если менеджер хотел бы быть уверенным в результате на 90% с предельной ошибкой ± 5%, то сколько покупателей необходимо отобрать в случайном порядке для получения такой оценки?

БИЛЕТ № 2

1.Статистическое определение вероятности, его особенности и связь с классическим определением.

2.Точечная оценка генеральной дисперсии. “Исправленные” выборочные дисперсия и среднее квадратическое отклонение.

3.Задачи.

Сколько различных «слов», каждое из которых содержит 4 буквы, можно составить из букв слова «экзамен»?

Владелец хлебного магазина заметил,, что у него ежедневно остается некоторое количество непроданных батонов и он решил оценить потребность в данном сорте хлеба. В течение месяца он записывал данные о числе проданных батанов и через 30 дней он установил, что в среднем продается 120 батонов со средним квадратическим отклонением в 10 батонов. Предположим, что ежедневные продажи батонов подчиняются нормальному распределению. Постройте 90% доверительный интервал для требуемого количества батонов.

БИЛЕТ № 3

1.Классическое определение вероятности. Свойства вероятности, вытекающие из классического определения. Примеры.

2.Моменты распределения. Начальные и центральные моменты. Асимметрия и эксцесс.

3.Задачи.

Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность первого автомата вдвое больше производительность второго автомата. Первый автомат производит в среднем 60% деталей отличного качества, а второй 84% деталей отличного качества. Наудачу взятая с конвейера деталь оказалась отличного качества Найти вероятность того, что эта деталь изготовлена первым автоматом? Вторым автоматом?

Ректорат университета хотел бы знать мнение студентов о новом учебном корпусе. Из 500 опрошенных студентов, 350 ответили, что им нравится новый корпус. Постройте 90% доверительный интервал доли студентов, которым понравился новый учебный корпус.

БИЛЕТ № 4

1. Вероятности суммы и произведения событий.

2. Проверка гипотезы о равенстве двух дисперсий нормально распределенных генеральных совокупностей. Сравнение исправленной выборочной дисперсии с предполагаемой генеральной дисперсией нормальной совокупности.

3.Задачи.

В магазин поступила партия микрокалькуляторов трех разных фирм – производителей. Продукция 1-ой фирмы составила-20%, 2-ой фирмы – 46% и 3-ей – 34%. Из опыта известно, что в гарантийный срок требуют ремонта 3% микрокалькуляторов 1-ой фирмы, 2% - 2-ой фирмы и 1% - 3-ей фирмы. Какова вероятность того, что микрокалькулятор, потребовавший ремонта в гарантийный срок, был изготовлен первой фирмой-производителем?

Для выяснения возрастных особенностей кадрового состава продавцов универсама было произведено обследование, в результате которого получены следующие данные:

Определите:

1) средний возраст продавцов;

2) дисперсию возраста продавцов;

3) коэффициент вариации.

БИЛЕТ №5

1. Формула полной вероятности. Формулы Байеса.

2. Сравнение выборочной средней и предполагаемой и генеральной средней нормальной совокупности при известной и неизвестной генеральной дисперсии; проверка гипотез о равенстве двух долей.

3.Задачи.

Компьютерная фирма продает мониторы 4 марок. При этом известно, что мониторы Sony составляют 24% от продаж, Panasonic-28%, LG – 16%, Samsung-32%. Вероятность неполадок в первый год работы для мониторов Sony составляет 0,01, Panasonic-0,02, LG – 0,03, Samsung-0,02. Какова вероятность неполадок в первый год работы монитора?

В молочном отделе универсама произведено контрольное взвешивание десяти 200-грамовых пачек сливочного масла и установлено, что 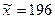г. и S=4г. Менеджер отдела выдвигает предположение о недобросовестности поставщика. Прав ли он? Уровень значимости принять равным 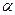=0,001.

ВОПРОСЫ К ЭКЗАМЕНУ (ЗАЧЕТУ)

Date: 2015-05-08; view: 2907; Нарушение авторских прав