
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тема 7. Выборочный метод и его значение в экономических исследованиях
|
|
1.Средняя ошибка выборки для доли при бесповторном собственно – случайном отборе может быть найдена как:
А)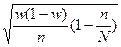 ; ;
| Б) 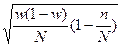 ; ;
| В) 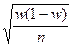 ; ;
| Г) 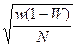 . .
|
2. Средняя ошибка выборки для доли при повторном собственно – случайном отборе может быть найдена как:
А)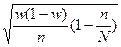 ; ;
| Б) 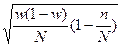 ; ;
| В) 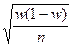 ; ;
| Г) 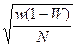 . .
|
3. Средняя ошибка выборки для средней при повторном собственно – случайном отборе может быть найдена как:
А)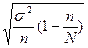 ; ;
| Б) 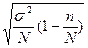 ; ;
| В) 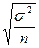 ; ;
| Г) 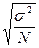 . .
|
4. Средняя ошибка выборки для средней при бесповторном собственно – случайном отборе может быть найдена как:
А)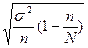 ; ;
| Б) 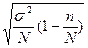 ; ;
| В) 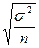 ; ;
| Г) 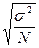 . .
|
5. Точечной оценкой генеральной дисперсии при объеме выборке 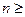 30 является:
30 является:
А) 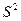 ; ;
| Б) 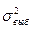 ; ;
| В) 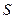 ; ;
| Г) 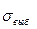 . .
|
6. Точечной оценкой генеральной дисперсии при объеме выборке n <30 является:
А) 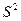 ; ;
| Б) 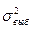 ; ;
| В) 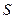 ; ;
| Г) 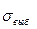 . .
|
7. Доверительный интервал для оценки генеральной средней при собственно-случайной бесповторной выборке объемом 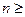 30 может быть записан как:
30 может быть записан как:
А) 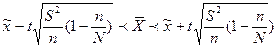 ; ;
| В) 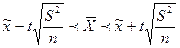 ; ;
|
Б) 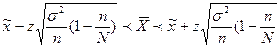 ); );
| Г) 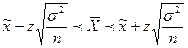 ; ;
|
8. Доверительный интервал для оценки генеральной средней при собственно-случайной повторной выборке объемом 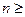 30 может быть записан как:
30 может быть записан как:
А) 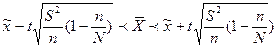 ; ;
| В) 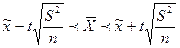 ; ;
|
Б) 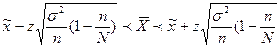 ); );
| Г) 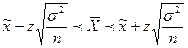 ; ;
|
9. Доверительный интервал для оценки генеральной средней при собственно-случайной повторной выборке объемом n <30 может быть записан как:
А) 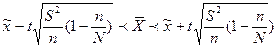 ; ;
| В) 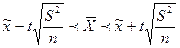 ; ;
|
Б) 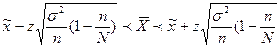 ); );
| Г) 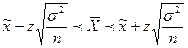 ; ;
|
10. Доверительный интервал для оценки генеральной средней при собственно-случайной бесповторной выборке объемом n <30 может быть записан как:
А) 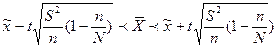 ; ;
| В) 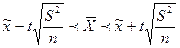 ; ;
|
Б) 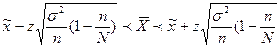 ); );
| Г) 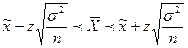 ; ;
|
11. Доверительный интервал для оценки генеральной доли при собственно-случайной бесповторной выборке объемом 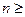 30 может быть записан как:
30 может быть записан как:
А) 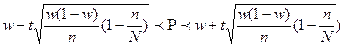
| В) 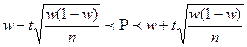
|
Б) 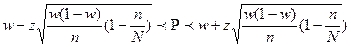
| Г) 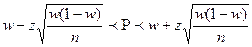
|
12. Доверительный интервал для оценки генеральной доли при собственно-случайной повторной выборке объемом 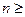 30 может быть записан как:
30 может быть записан как:
А) 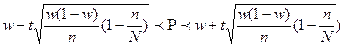
| В) 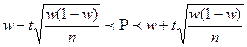
|
Б) 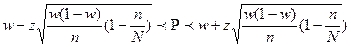
| Г) 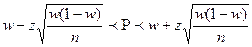
|
13. Доверительный интервал для оценки генеральной доли при собственно-случайной повторной выборке объемом n <30 может быть записан как:
А) 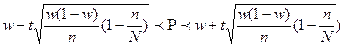
| В) 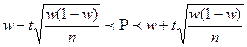
|
Б) 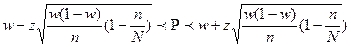
| Г) 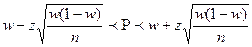
|
14. Доверительный интервал для оценки генеральной доли при собственно-случайной бесповторной выборке объемом n <30 может быть записан как:
А) 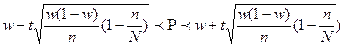
| В) 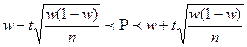
|
Б) 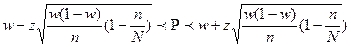
| Г) 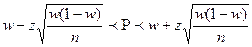
|
15. Необходимый объем выборки для оценки генеральной средней при собственно- случайном бесповторном отборе может быть найден как:
А) 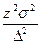 ; ;
| Б) 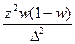 ; ;
| В) 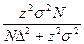 ; ;
| Г) 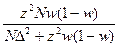 ; ;
|
16. Необходимый объем выборки для оценки генеральной средней при собственно- случайном повторном отборе может быть найден как:
А) 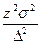 ; ;
| Б) 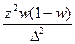 ; ;
| В) 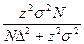 ; ;
| Г) 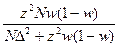 ; ;
|
17. Необходимый объем выборки для оценки генеральной доли при собственно- случайном бесповторном отборе может быть найден как:
А) 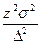 ; ;
| Б) 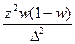 ; ;
| В) 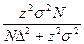 ; ;
| Г) 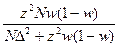 ; ;
|
18. Необходимый объем выборки для оценки генеральной средней при собственно- случайном повторном отборе может быть найден как:
А) 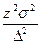 ; ;
| Б) 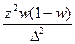 ; ;
| В) 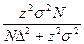 ; ;
| Г) 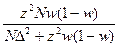 ; ;
|
19. Каким законом распределения вероятностей описываются малые выборки?
| А) нормальным; | Б) 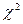 - Пирсона; - Пирсона;
| В) F- Фишера; | Г) t – Cтьюдента. |
Тема 8. Статистическая проверка гипотез
1. Какая из данных гипотез является непараметрической:
А) гипотеза о числовом значении доли;
Б) гипотеза о равенстве двух генеральных средних;
В) гипотеза о равенстве двух генеральных дисперсий;
Г) гипотеза о нормальном распределении генеральной совокупности.
2. Статистическая гипотеза называется параметрической, если в ней сформулированы предположения относительно:
А) вида закона распределения;
Б) неизвестных значений параметров распределения определенного вида;
В) уровня значимости;
Г) известных значений параметров распределения определенного вида.
3. Статистическая гипотеза называется непараметрической, если в ней сформулированы предположения относительно:
А) вида закона распределения;
Б) неизвестных значений параметров распределения определенного вида;
В) уровня значимости;
Г) известных значений параметров распределения определенного вида.
4.При постановке задачи обязательно формулируют Н1, которую называют:
| А) основной гипотезой; | Б) базовой гипотезой; | В) альтернативной гипотезой; | Г) первой гипотезой. |
5. Критическая область – это:
| А) область допустимых значений критерия; | В) область принятия нулевой гипотезы; |
| Б) совокупность значений критерия, при которых нулевую гипотезу отвергают; | Г) совокупность значений критерия, при которых нулевую гипотезу нельзя отвергнуть. |
6. Область допустимых значений – это:
| А) критическая область; | В) область принятия альтернативной гипотезы; |
| Б) совокупность значений критерия, при которых нулевую гипотезу отвергают; | Г) совокупность значений критерия, при которых нулевую гипотезу нельзя отвергнуть. |
7. Критические области бывают:
| А) только односторонними; | В) только трехсторонними; |
| Б) только двухсторонними; | Г)одно- или двухсторонними. |
8. Допустить ошибку первого рода - это значит:
| А) отвергнуть нулевую гипотезу если она верна; | В) отвергнуть нулевую гипотезу если она неверна; |
| Б) принять нулевую гипотезу если она верна; | Г) принять нулевую гипотезу если она неверна. |
9. Если конкурирующая гипотеза имеет вид 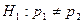 , то критическая область:
, то критическая область:
| А) правосторонняя; | Б) левосторонняя; | В) двухсторонняя; | Г) трехсторонняя. |
10. Если конкурирующая гипотеза имеет вид 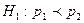 , то критическая область:
, то критическая область:
| А) правосторонняя; | Б) левосторонняя; | В) двухсторонняя; | Г) трехсторонняя. |
11. Если конкурирующая гипотеза имеет вид 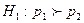 , то критическая область:
, то критическая область:
| А) правосторонняя; | Б) левосторонняя; | В) двухсторонняя; | Г) трехсторонняя. |
Date: 2015-05-08; view: 1629; Нарушение авторских прав