
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тема 2. Основные определения, понятия и теоремы теории вероятностей
|
|
1. Классическое определение вероятности гласит:
А) вероятностью события А называют отношение числа исходов благоприятствующих наступления этого события, к общему числу всех равновозможных и несовместных событий;
Б) вероятностью события А называют отношение числа исходов благоприятствующих наступления этого события, к общему числу всех единственно возможных и равновозможных событий;
В) вероятностью события А называют отношение числа исходов благоприятствующих наступления этого события, к общему числу всех единственно возможных, равновозможных и несовместных событий;
Г) вероятностью события А называют отношение числа исходов благоприятствующих наступления этого события, к общему числу всех единственно возможных событий;
2. Статистической вероятностью события А называется:
А) относительная частота (частость) этого события, вычисленная по результатам большого числа испытаний;
Б) частота этого события, вычисленная по результатам испытаний;
В) частота этого события, вычисленная по результатам большого числа испытаний;
Г) относительная частота (частость) этого события, вычисленная по результатам небольшого числа испытаний.
3. Согласно свойствам вероятности, вытекающим из классического определения, вероятность достоверного события равна:
| А) нулю | Б) единице | В) двум | Г) трем |
4. Согласно свойствам вероятности, вытекающим из классического определения, вероятность невозможного события равна:
| А) нулю | Б) единице | В) двум | Г) трем |
5. Согласно свойствам вероятности, вытекающим из классического определения, вероятность события находится в интервале:
А) 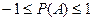
| Б) 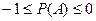
| В) 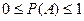
| Г) 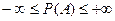
|
6. Согласно свойствам вероятности, вытекающим из классического определения, сумма вероятностей противоположных событий равна:
А) 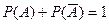
| Б) 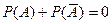
| В) 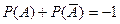
| Г) 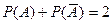
|
7. Теорема сложения двух совместных событий может быть записана как:
А) 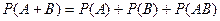
| В) 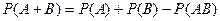
|
Б) 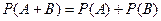
| Г) 
|
8. Теорема сложения двух несовместных событий может быть записана как:
А) 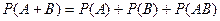
| В) 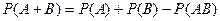
|
Б) 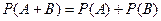
| Г) 
|
9. Теорема умножения двух зависимых событий может быть записана как:
А) 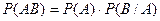
| В) 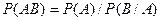
|
Б) 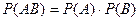
| Г) 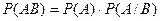
|
10. Теорема умножения двух независимых событий может быть записана как:
А) 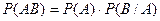
| В) 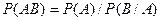
|
Б) 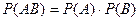
| Г) 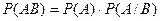
|
11. Вероятность совместного появления нескольких событий, независимых в совокупности, равна:
А) 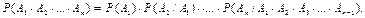
| В) 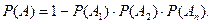
|
Б) 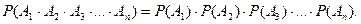
| Г) 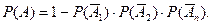
|
12. Вероятность совместного появления нескольких событий, зависимых в совокупности, равна:
А) 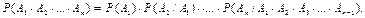
| В) 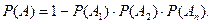
|
Б) 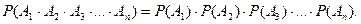
| Г) 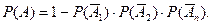
|
13. Вероятность появления хотя бы одного события из n независимых в совокупности равна:
А) 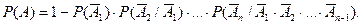
| В) 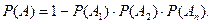
|
Б) 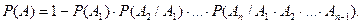
| Г) 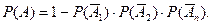
|
14. Вероятность появления хотя бы одного события из n зависимых в совокупности равна:
А) 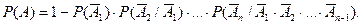
| В) 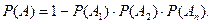
|
Б) 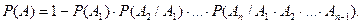
| Г) 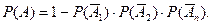
|
Date: 2015-05-08; view: 1077; Нарушение авторских прав