
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тема 4. Случайные величины
|
|
1. Случайная величина – это
А) величина, которая в результате опыта (испытания, эксперимента) принимает одно из своих возможных значений, причем заранее неизвестно какое именно;
Б) величина, которая в результате опыта (испытания, эксперимента) принимает одно из своих возможных значений, причем заранее известно какое именно;
В) величина, которая в результате опыта (испытания, эксперимента) принимает несколько из своих возможных значений, причем заранее неизвестно какие именно;
Г) величина, которая в результате опыта (испытания, эксперимента) принимает несколько из своих возможных значений, причем заранее известно какие именно;
2.Формула Бернулли записывается как:
А) 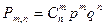 ; ;
| Б) 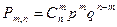 ; ;
| В) 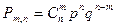 ; ;
| Г) 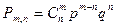 . .
|
3. Математическое ожидание биномиального распределения рассчитывается как:
А) 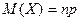 ; ;
| Б) 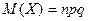 ; ;
| В) 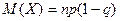 ; ;
| Г) 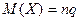 . .
|
4. Дисперсия биномиального распределения рассчитывается как:
А) 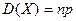 ; ;
| Б) 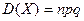 ; ;
| В) 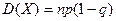 ; ;
| Г) 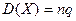 . .
|
5. Среднее квадратическое отклонение биномиального распределения рассчитывается как:
А) 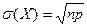 ; ;
| Б) 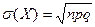 ; ;
| В) 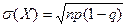 ; ;
| Г) 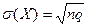 . .
|
6. Вероятнейшая частота (наивероятнейшее число) наступления событий рассчитывается как:
А) 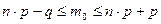 ; ;
| В) 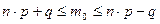 ; ;
|
Б) 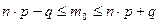 ; ;
| Г) 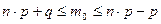 . .
|
7.Формула распределения вероятностей Пуассона записывается как:
А) 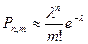 ; ;
| Б) 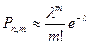 ; ;
| В) 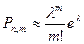 ; ;
| Г) 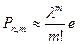 . .
|
8. Математическое ожидание СВ, распределенной по закону Пуассона рассчитывается как:
А) 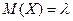 ; ;
| Б) 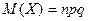 ; ;
| В) 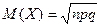 ; ;
| Г) 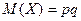 . .
|
9. Дисперсия СВ, распределенной по закону Пуассона рассчитывается как:
А) 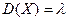 ; ;
| Б) 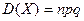 ; ;
| В) 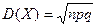 ; ;
| Г) 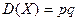 . .
|
10. Формула гипергеометрического закона распределения ДСВ:
А) 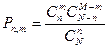 ; ;
| Б) 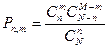 ; ;
| В) 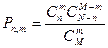 ; ;
| Г) 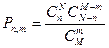 ; ;
|
11. Математическое ожидание СВ, распределенной по гипергеометрическом закону:
А) 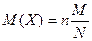 ; ;
| Б) 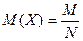 ; ;
| В) 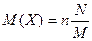 ; ;
| Г) 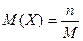 . .
|
12. Дисперсия СВ, распределенной по гипергеометрическом закону определяется как:
А) 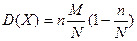 ; ;
| В) 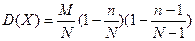 ; ;
|
Б) 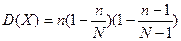 ; ;
| Г) 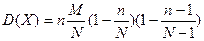 . .
|
13. Математическое ожидание НСВ равно:
А) 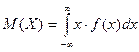 ; ;
| Б) 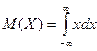 ; ;
| В) 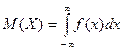 ; ;
| Г) 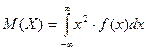
|
14. Нормальная СВ имеет плотность распределения, определяемую формулой:
А) 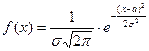 ; ;
| В) 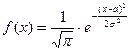 ; ;
|
Б) 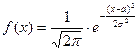 ; ;
| Г) 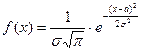 ; ;
|
15. Стандартная (нормированная) нормальная СВ имеет плотность распределения, определяемую формулой:
А) 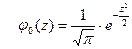 ; ;
| В) 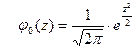 ; ;
|
Б) 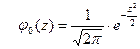 ; ;
| Г) 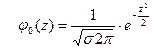 . .
|
16. Согласно свойствам плотности распределения стандартной (нормированной) нормальной СВ:
| А) функция четная; | Б) функция нечетная; | В)функция отрицательная; | Г) функция положительная; |
17. Функция Лапласа имеет вид:
А) 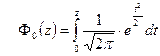 ; ;
| В) 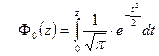 ; ;
|
Б) 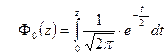 ; ;
| Г) 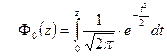 . .
|
18. Интегральная теорема Лапласа записывается как:
А) 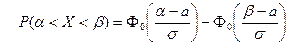 ; ;
| В) 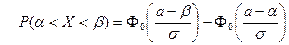 ; ;
|
Б) 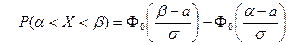 ; ;
| Г) 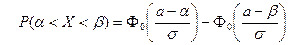 . .
|
19. Вероятность заданного отклонения нормально распределенной СВ от ее математического ожидания на величину меньшую Δ равна:
А) 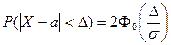
| В) 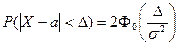
|
Б) 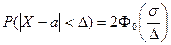
| Г) 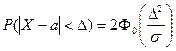
|
20. Локальная теорема Лапласа записывается как:
А) 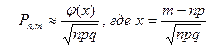
| В) 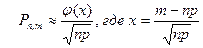
|
Б) 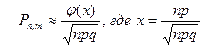
| Г) 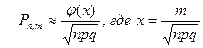
|
21. Аппроксимация биномиального распределения с использованием нормального позволяет определять вероятность того, что ДСВ попадет в заданный интервал как:
А) 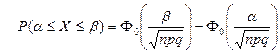 ; ;
| В) 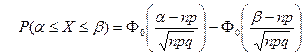
|
Б) 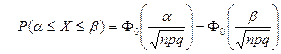 ; ;
| Г) 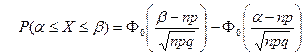
|
Date: 2015-05-08; view: 1122; Нарушение авторских прав