Задачи к теме 5 «Законы распределения непрерывных случайных величин»

1. Компьютерная система содержит 50 одинаковых микрочипов. Вероятность того, что любой микрочип будет работать в заданное время, равна 0,9. Для выполнения некоторой операции требуется, чтобы, по крайней мере, 30 микрочипов было в рабочем состоянии.

а) Чему равна вероятность того, что операция будет выполнена успешно?

б) Чему равна вероятность того, что будут работать 47 микрочипов?

2. Почтовое отделение быстро оценивает объём переводов в рублях, взвешивая почтовые отправления, полученные в течение каждого текущего рабочего дня. Установлено, что если вес почтовых отправлений составляет N кг, то объём переводов в рублях есть случайная величина, распределенная по нормальному закону со средним значением 160N и стандартным отклонением 20N руб. Найти вероятность того, что в день, когда вес почтовых отправлений составит 150 кг, объём переводов в рублях будет находиться в пределах:

а) от 21000 до 27000 руб.; б) более 28500 руб.; в) менее 22000 руб.

3.Менеджер крупного ресторана по опыту знает, что только 80% людей, сделавших заказ на вечер, придут в ресторан поужинать. В один из вечеров менеджер решил принять 60 заказов, хотя в ресторане было лишь 55 свободных столиков. Чему равна вероятность того, что более 55 посетителей придут на заказанные места?

4. Экзамен по математической статистике успешно сдают 75% студентов дневного отделения. Если на втором курсе факультета обучается 250 студентов, то какова вероятность того, что 203 студента сдадут экзамен успешно?

5. В отделе продаж страховой компании работают 45 сотрудников. Вероятность того, что сотрудник выполнит план по числу заключенных договоров, оценивается начальником отдела как 0,7. Какова вероятность того, что:

а) план выполнят как минимум 35 сотрудников?

б) план выполнят не более 30 сотрудников?

в) план выполнят 37 сотрудников?

6. Отдел маркетинга фармацевтической компании утверждает, что новая модификация таблеток от головной боли используется 30% пациентов. Если среди пациентов было отобрано 80 человек, то какова вероятность того, что доля лиц в выборке, предпочитающих новую модификацию таблеток, не будет отличаться по абсолютной величине от истинной доли более чем на 0,1?

7. Дневная выручка супермаркета распределена по нормальному закону с математическим ожиданием 10000 у.е. и стандартным отклонением 1400 у.е. Найдите вероятность того, что:

а) выручка супермаркета окажется более 13000 у.е.;

б) выручка супермаркета окажется менее 8000 у.е.;

в) найдите границы, в которых будет находиться выручка супермаркета согласно правилу трех сигм.

8. По данным независимого исследования, хлеб определенного сорта, составляет 15% от совокупной реализации хлебобулочных изделий. Если выборочному обследованию были подвергнуты 80 торговых предприятий, то какова вероятность того, что доля реализации хлеба определенного сорта в генеральной совокупности будет отличаться по абсолютной величине от истинной доли менее чем на 5%?

9. В течение месяца кредитным отделом банка было выдано 68 ипотечных кредитов. Менеджер банка оценивает вероятность просрочки оплаты таких кредитов как 0,2. Какова вероятность того, что в течение срока кредитования будут просрочены:

а) как минимум 15 кредитов?

б) не более 18 кредитов?

в) 16 кредитов?

10. Фирма, занимающаяся продажей товаров по каталогу, ежемесячно получает по почте заказы. Число этих заказов - нормально распределенная случайная величина со средним квадратическим отклонением 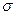= 560 и неизвестным математическим ожиданием. В 90% случаев число ежемесячных заказов превышает 12439. Найдите ожидаемое среднее число заказов, получаемых фирмой за месяц.

11. Дневная добыча угля в некоторой шахте распределена по нормальному закону с математическим ожиданием 870 тонн и стандартным отклонением 90 тонн.

а) Найдите вероятность того, что в определенный день будут добыты по крайней мере 900 тонн угля.

б) Определите долю рабочих дней, в которые будет добыто от 860 до 940 тонн угля.

в) Найдите вероятность того, что в данный день добыча угля окажется ниже 750 тонн.

12. Кандидат на выборах считает, что 20% избирателей в определенной области поддерживают его избирательную платформу. Если 72 избирателя случайно отобраны из числа избирателей данной области, найдите вероятность того, что выборочная доля избирателей, поддерживающих кандидата, не будет отличаться по абсолютной величине от истинной доли более, чем на 0,09.

13. Еженедельный выпуск продукции на заводе приблизительно распределен по нормальному закону со средним значением, равным 150000 единиц продукции в неделю, и стандартным отклонением - 12000 ед. Найдите вероятность того, что еженедельный выпуск продукции:

а) превысит 170000 единиц;

б) окажется ниже 100000 единиц в данную неделю?

в) Предположим, что возникли трудовые споры, и недельный выпуск продукции стал ниже 90000 ед. Менеджеры обвиняют профсоюз в беспрецедентном падении выпуска продукции, а профсоюз утверждает, что выпуск продукции находится в пределах принятого уровня (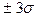). Можно ли доверять профсоюзу?

14. Вес тропического грейпфрута, выращенного в Краснодарском крае, - нормально распределенная случайная величина с неизвестным математическим ожиданием и дисперсией, равной 0,09. Агрономы знают, что 75% фруктов весят меньше, чем 0,5 кг. Найдите ожидаемый вес случайно выбранного грейпфрута.

15. Один из методов, позволяющих добиться успешных экономических прогнозов, состоит в применении согласованных подходов к решению конкретной проблемы. Обычно прогнозом занимается большое число аналитиков. Средний результат таких индивидуальных прогнозов представляет собой общий согласованный прогноз. Пусть этот прогноз относительно величины банковской процентной ставки в текущем году подчиняется нормальному закону со средним значением а = 11% и стандартным отклонением 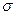= 3,6%. Из группы аналитиков случайным образом отбирается один человек. Найдите вероятность того, что согласно прогнозу этого аналитика уровень процентной ставки:

а) превысит 13%;

б) окажется менее 16%;

в) будет в пределах от 13 до 17%.

16. Предположим, что в течение года цена на акции некоторой компании есть случайная величина, распределенная по нормальному закону с математическим ожиданием, равным 50 условным денежным единицам, и стандартным отклонением, равным 10. Чему равна вероятность того, что в случайно выбранный день обсуждаемого периода цена за акцию будет:

а) более 70 условных денежных единиц?

б) ниже 50 за акцию?

в) между 45 и 58 условными денежными единицами за акцию?

17. По данным университета лишь 45% абитуриентов получают положительные оценки на вступительных экзаменах. Предположим, что в приемную комиссию поступило 2120 заявлений. Чему равна вероятность того, что:

а) хотя бы 970 абитуриентов получат положительные оценки на вступительных экзаменах?

б) 950 абитуриентов получат положительные оценки на вступительных экзаменах?

18. Средний срок службы коробки передач до капитального ремонта у автомобиля определенной марки составляет 56 месяцев со стандартным отклонением 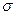= 16 мес. Привлекая покупателей, производитель хочет дать гарантию на этот узел, обещая сделать ремонт коробки передач нового автомобиля в случае ее поломки до определенного срока. Пусть срок службы коробки передач подчиняется нормальному закону. На сколько месяцев в таком случае производитель должен дать гарантию для этой детали, чтобы число бесплатных ремонтов не превышало 2,275% проданных автомобилей?

19. При производстве безалкогольных напитков специальный аппарат разливает определенное число унций (1 унция = 28,3 г) напитка в стандартную ёмкость. Число разлитых унций подчиняется нормальному закону с математическим ожиданием, зависящим от настройки аппарата. Количество унций напитка, разлитых отдельным аппаратом, имеет стандартное отклонение s = 0,4 унции. Пусть ёмкости объёмом в 8 унций наполняются кока-колой. Сколько унций напитка должен в среднем разливать аппарат, чтобы не более 3% ёмкостей оказались переполненными?

20. Налоговая инспекция утверждает, что нарушения налогового законодательства характерны для 35% предприятий города. Тщательной проверке были подвергнуты 59 предприятий. Чему равна вероятность того, что доля предприятий – нарушителей будет отличаться от истинной доли более чем на 0,12?

Date: 2015-05-08; view: 1991; Нарушение авторских прав