
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Давление – величина, равная отношению элементарной силы, действующей на элемент поверхности нормально к ней, к элементарной площади этого элемента
|
|
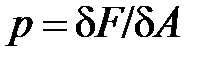
(символом 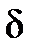 принято обозначать элементарность величины, в отличие от символа дифференциала d, который означает малое приращение, изменение величины).
принято обозначать элементарность величины, в отличие от символа дифференциала d, который означает малое приращение, изменение величины).
При равномерном распределении силы  по поверхности площадью
по поверхности площадью  давление выражается формулой:
давление выражается формулой:
 .
.
Единица давления СИ: 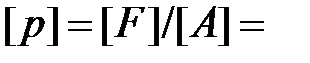 1 H/1 м2 = 1 Па.
1 H/1 м2 = 1 Па.
Единице давления СИ присвоено специальное наименование паскаль (Па) в честь французского математика Блеза Луи Паскаля (1623 –1662).
Паскаль равен давлению, вызываемому силой 1 Н, равномерно распределённой по поверхности площадью 1 м 2 , расположеннойперпендикулярно силе.
Давление 1 Па по сравнению с атмосферным давлением очень маленькая величина и для практического пользования используется внесистемная единица бар
1 бар = 105 Па = 0,1 МПа 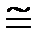 750 мм рт. ст.
750 мм рт. ст.
В технической литературе прошлых лет издания, а также при проведении измерений использовались (и до сих пор используются, хотя не рекомендуются) в качестве единицы давления техническая атмосфера (единица системы МКГСС) и внесистемные единицы: бар, физическая атмосфера (атмосфера физическая); мм рт. ст., мм вод. ст., мм сп. ст. (с помощью последних измеренное давление сравнивают с давлением столба жидкости – воды, ртути, спирта).
Связь между различными единицами давления следующая:
1 атмосфера техническая = 1 ат = 1 кгс/см2 =
= 0,981×105 Па = 735,6 мм рт. ст. = 10 м вод. ст.,
1 ат = 1 кгс/см2 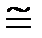 0,1 МПа;
0,1 МПа;
1 атмосфера физическая = 1 атм = 760 мм рт. ст. =
= 101325 Па = 1,033 ат = 10,33 м вод.ст.,
1 атм = 760 мм рт. ст. = 101325 Па;
1 мм вод. ст. = 9,81 Па; 1 мм рт. ст. = 133,322 Па.
Различают абсолютное давление 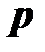 (в дальнейшем – просто давление, см. приложение Б), атмосферное или барометрическое давление
(в дальнейшем – просто давление, см. приложение Б), атмосферное или барометрическое давление 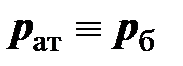 , измеряемое барометром, избыточное давление
, измеряемое барометром, избыточное давление 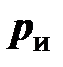 , измеряемое манометром, и разрежение
, измеряемое манометром, и разрежение 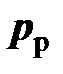 (не следует применять термин «вакуум» вместо разрежения, т. к. вакуум не является физической величиной), измеряемое вакуумметром.
(не следует применять термин «вакуум» вместо разрежения, т. к. вакуум не является физической величиной), измеряемое вакуумметром.
Термодинамическое (абсолютное) давление в сосуде
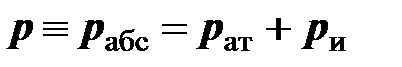 .
.
Избыточным давлением называется разность между давлением газа в сосуде и атмосферным давлением:
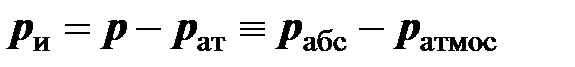 .
.
Если давление в сосуде меньше атмосферного, то разность между атмосферным давлением и давлением в сосуде называется разрежением
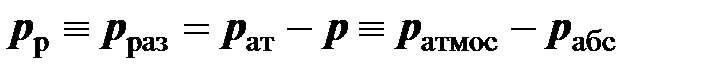 .
.
Из этой формулы видно, что минимальное разрежение равно нулю (давление в сосуде равно атмосферному), а максимальное – атмосферному (давление в сосуде равно нулю). Поскольку атмосферное давление не постоянно, то и максимальное разрежение не является постоянной величиной. Возникает вопрос: может ли вакуумметр показать разрежение больше 760 мм рт. ст? Ответ: может, если атмосферное давление в момент измерения превышает 760 мм рт. ст.
На рисунке 1 представлена графическая связь между рассмотренными видами давления, а на рисунке 2 показаны способы их измерения.


Рисунок 2 – Способы измерения давлений
Температура. Температура характеризует степень нагретости тела (интенсивность хаотического, теплового движения микрочастиц тела). Непосредственно измерить температуру пока не удаётся. Однако с изменением температуры изменяются многие свойства тел, которые относительно легко измерить, например, объём, давление, электрическое сопротивление и другие (как уже отмечалось, наименования физических величин – количественных характеристик свойств тел – могут совпадать с наименованиями самих свойств, которые и измеряются в опытах.). Изобретение термометра (первого
измерительного теплового прибора) можно рассматривать как начало
развития термодинамики, так как понятие температуры является основным в учении о тепловых процессах.
В 1592 году Галилейво время лекции демонстрировал прообраз термометра (термоскопа). Термометр Галилея состоял из стеклянного шара, наполненного воздухом; от нижней части шара отходила трубка, частично заполненная водой, которая заканчивалась в сосуде с водой. Когда воздух в шаре нагревался или охлаждался, уровень воды в стеклянной трубке изменялся, что служило указанием на отклонение температуры от первоначального значения.
Наряду с термоскопом Галилео Галилей (1564 – 1642) сконструировал телескоп 32 x увеличения, с помощью которого он разрушил догмат о совершенстве небесных тел: на Солнце оказались пятна, Луна – с кратерами, Млечный путь распался на отдельные звёзды. Всё видимое им стали считать оптическим обманом. Суд инквизиции принудил его отречься от своих «заблуждений». Через пять лет после процесса Галилей издал свой основной труд «Беседы о двух новых науках», где его научные взгляды остались непоколебимы.
Слова, произнесённые им согласно легенде сразу после отреченья: «И всё-таки она вертится!» (Земля вокруг своей оси и Солнца, а не Солнце вокруг неподвижной Земли), – стали синонимом борьбы за научную истину.
Первый современный термометр был описан в 1724 г. немецким физиком Д. Фаренгейтом (1686 – 1736). За начало шкалы (нуль температуры) он предложил принять температуру таяния смеси льда с нашатырём или поваренной солью (которая оказалась равной минус 17,8 оС). Вторую точку он получил, погружая термометр в смесь льда и воды. Интервал между этими двумя точками он разделил на 32 части. В качестве третьей опорной точки он брал температуру человека, которую он округлил до 96 единиц (величины, кратной 32), что равняется 35,6 оС (одни исследователи считают, что это была температура здорового человека, которая постепенно приняла значение 36,6 оС в наши дни, а другие,– что в качестве «эталона» был взят человек, которого знобило).
В качестве четвёртой опорной точки он брал температуру кипения воды, составившую 212 единиц (градусов). Таким образом, интервал от точки таяния льда до точки кипения воды по шкале Фаренгейта равен 180о. Применяют термометры со шкалой Фаренгейта (рисунок 3) в англоязычных странах (Великобритания, США, Канада и др.). Читая английские книги, не следует удивляться, что температура ребенка 98оне вызывает тревоги у матери, а температура минус 60о не является такой уж редкой на Аляске.
Во Франции в употребление вошла шкала Р. Реомюра (1683 – 1757), предложенная им в 1730 году. В этой шкале в качестве реперных точек выбраны температура таяния льда и кипения воды при нормальном давлении в 1 атмосферу. Интервал между этими точками разбит на 80 частей и 1/80 часть представляет собой градус Реомюра. До революции в России была принята шкала Реомюра – термометры Реомюра висели на улицах и во всех домах. Лишь в тридцатых годах они были вытеснены термометрами Цельсия. В настоящее время шкала Реомюра не применяется.

В 1742 году шведский физик А. Цельсий (1701 – 1744) разделил интервал между температурами плавления льда и кипения воды на 100 частей. Точке кипения воды он присвоил при этом значение температуры, равное 0, точке плавления льда – 100. В 1750 г. Трёмер переменил местами числа градусов у температуры плавления и кипения воды. Эта шкала получила название стоградусной термодинамической температурной шкалы или шкалы Цельсия (см. рисунок 3).
Рисунок 3 – Температурные шкалы
Жидкостные термометры, заполненные ртутью или этиловым спиртом, а при низких температурах – пентаном, применяют и в настоящее время, несмотря на присущие им недостатки, связанные с зависимостью их показаний от свойств термометрического вещества (с зависимостью температурного коэффициента объёмного расширения от температуры).
Особое место занимают газовые термометры, в которых термометрическим веществом являются газы (азот, водород, гелий) при малых давлениях. Принцип действия газовых термометров основан на линейной зависимости объёма газа от температуры при постоянном давлении, устанавливаемой законом Гей-Люссака
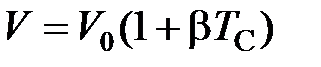 ,(2.1)
,(2.1)
где 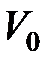 – объём при температуре Цельсия
– объём при температуре Цельсия 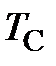 = 0 оС;
= 0 оС;
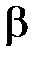 = 1/273,15 K–1 = 0,003661 K–1 – температурный коэффициент объёмного расширения газа при постоянном давлении, остающийся практически постоянным в большом интервале температур при малом давлении для многих газов.
= 1/273,15 K–1 = 0,003661 K–1 – температурный коэффициент объёмного расширения газа при постоянном давлении, остающийся практически постоянным в большом интервале температур при малом давлении для многих газов.
| Рисунок 4 – Температурные шкалы Кельвина и Цельсия |
 Процесс, протекающий при постоянном давлении, называется изобарным. Для газа такой процесс для различных давлений в соответствии с зависимостью (2.1) изобразится прямыми линиями в диаграмме
Процесс, протекающий при постоянном давлении, называется изобарным. Для газа такой процесс для различных давлений в соответствии с зависимостью (2.1) изобразится прямыми линиями в диаграмме 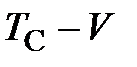 (рисунок 4). Все изобары пересекают ось
(рисунок 4). Все изобары пересекают ось 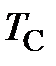 в одной и той же точке
в одной и той же точке 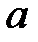 , определяемой из условия
, определяемой из условия 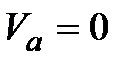 или
или 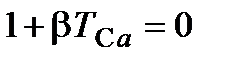 , откуда
, откуда
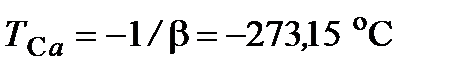 .
.
Сместив начало отсчёта температур в эту точку, мы перейдём от шкалы температур по Цельсию к другой температурной шкале, которая называется абсолютной термодинамической шкалой или шкалой Кельвина. Температуру, отсчитанную по такой шкале, стали называется абсолютной температурой (в настоящее время эту температуру принято называть термодинамической температурой).
Единица температуры в этой шкале получила наименование кельвин (К) в честь английского физика В.Томсона (1824 – 1907), который первым в 1848 году предложил отсчитывать температуру от абсолютного нуля (шкалу Кельвина). В 1892 году Вильяму Томсону был присвоен титул лорда Кельвина ( по имени речки Кельвин, протекающей вблизи университета в г. Глазго, где он преподавал) за научные заслуги при разработке первого трансатлантического кабеля (1856 – 1865).
Связь между температурой по шкале Кельвина 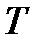 (термодинамической температурой) и температурой
(термодинамической температурой) и температурой 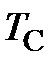 по шкале Цельсия (в дальнейшем температурой Цельсия) устанавливается соотношением (см. рисунок 4)
по шкале Цельсия (в дальнейшем температурой Цельсия) устанавливается соотношением (см. рисунок 4)
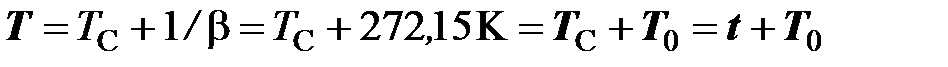 , (2.2)
, (2.2)
где 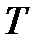 – термодинамическая температура (температура Кельвина), К;
– термодинамическая температура (температура Кельвина), К;
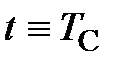 – температура Цельсия, оС;
– температура Цельсия, оС;
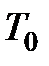 = 273,15 К – термодинамическая температура таяния льда.
= 273,15 К – термодинамическая температура таяния льда.
Таким образом, шкалы Кельвина и Цельсия смещены друг относительно друга так, что температура Цельсия находится как разность температур Кельвина
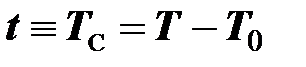 . (2.3)
. (2.3)
Единицы температур Цельсия и Кельвина равны по значению, так как характеризуют одну и ту же порцию измеряемого свойства (как будет показано далее – интенсивность хаотического движения отдельных молекул газа):
[ 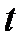 ] = [
] = [ 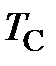 ] = 1 oC = [
] = 1 oC = [ 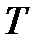 ] = 1 K,
] = 1 K,
следовательно, термины «градус Цельсия» и «кельвин» являются синонимичными наименованиями одной и той же порции измеряемого свойства.
Похожее положение раньше было с давлением, когда единица давления 1 кгс/см 2 = 1 ат имела синонимичные наименования: ата – атмосфера абсолютная – для абсолютного давления, ати – атмосфера избыточная – для избыточного давления. После введения единой единицы давления паскаля (Па) вид давления стал определяться не по наименованию соответствующей единицы давления (5 ат и – избыточное давление), а по наименованию данного вида давления, например, избыточное давление 5 МПа. Аналогичным образом следует выбрать единый термин для наименования единицы термодинамической температуры и температуры Цельсия, например, градус (град) или кельвин (применение кельвина в качестве наименования единицы отрицательной температуры Цельсия может вызвать затруднения), а виды температур различать по их наименованиям: температура Цельсия минус пять градусов (Т С = – 5 град = – 5о= – 5 К), температура Кельвина (термодинамическая) пять градусов (Т = 5 град = 5 о= 5 К).
Поэтому разность температур (температурный интервал) может выражаться как в кельвинах, так и в градусах Цельсия (см. рисунок 3):
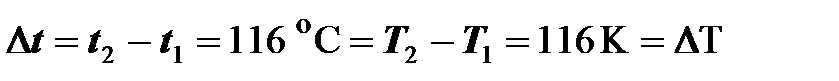 (2.4)
(2.4)
Для лучшего понимания сказанного можно провести аналогию между термодинамическим (абсолютным) давлением 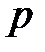 и термодинамической (абсолютной) температурой
и термодинамической (абсолютной) температурой 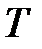 , между атмосферным давлением
, между атмосферным давлением 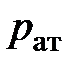 и температурой таяния льда
и температурой таяния льда 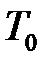 , избыточным давлением
, избыточным давлением 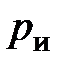 и температурой Цельсия
и температурой Цельсия 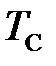 . Данные величины имеют аналогичную математическую
. Данные величины имеют аналогичную математическую
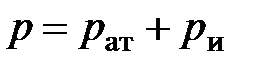
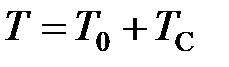

и графическую связь (рисунок 5).
Рисунок 5 – Аналогия между термодинамическими температурами и давлениями
Физический смысл температуры. Согласно кинетической теории газов средняя кинетическая энергия молекулы 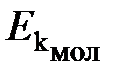 и термодинамическая температура газа связаны соотношением
и термодинамическая температура газа связаны соотношением
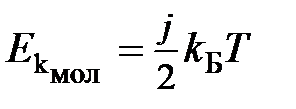 ,
,
где  – коэффициент пропорциональности, зависящий от числа атомов в молекуле, называется числом степеней свободы;
– коэффициент пропорциональности, зависящий от числа атомов в молекуле, называется числом степеней свободы;
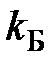 – постоянная Больцмана.
– постоянная Больцмана.
Если разделить кинетическую энергию молекулы на численное значение температуры 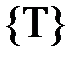 , то с учётом (1.17) получим единичную кинетическую энергию молекулы – энергию молекулы при единичной температуре (при Т = 1К)
, то с учётом (1.17) получим единичную кинетическую энергию молекулы – энергию молекулы при единичной температуре (при Т = 1К)
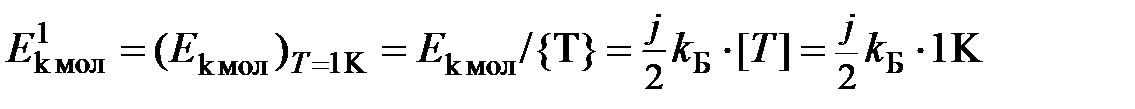
Отсюда 
и физический смысл температуры – термодинамическая температура показывает, во сколько раз кинетическая энергия молекулы газа в данном состоянии отличается от кинетической энергии молекулы при единичной температуре, принятой за основу (1 К). Если представить энергию молекулы при единичной температуре в виде энергетического кубика, то температура (численное значение) будет показывать число таких энергетических кубиков, составляющих энергию молекулы при этой температуре. Таким образом, температура 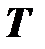 позволяет сравнить малые энергии молекул и их изменения (для одноатомного газа
позволяет сравнить малые энергии молекул и их изменения (для одноатомного газа 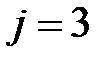 и
и 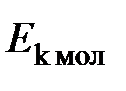 = 2,070987. 10 –23 Дж) в виде конечных значений, удобных для практики.
= 2,070987. 10 –23 Дж) в виде конечных значений, удобных для практики.
Количество вещества.Количество (совокупность) частиц (структурных единиц, элементов – атомов, молекул, ионов и т. п.), содержащихся в теле, характеризуется числом частиц, которое не имеет собственной единицы. Число частиц – величина, имеющая большое числовое значение даже для тел малой массы (например, водород массой 2 г содержит число молекул порядка 1023) и поэтому она мало пригодна для практических расчетов изменения запаса вещества в системе. Поэтому возникла необходимость задавать количество частиц системы не числом отдельных частиц, а числом укрупнённых порций таких частиц.
В качестве такой укрупнённоё порции частиц принято брать число атомов, содержащихся в порции изотопа углерода 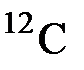 массой 0,012 кг (12 г). Это число частиц можно получить, если разделить массу
массой 0,012 кг (12 г). Это число частиц можно получить, если разделить массу 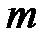 этой порции углерода на массу одного атома углерода
этой порции углерода на массу одного атома углерода
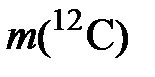 = 1,9926482×10 –26 кг – по данным на 1987 год [ГСССД 1-87],
= 1,9926482×10 –26 кг – по данным на 1987 год [ГСССД 1-87],
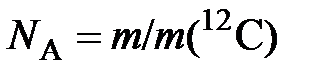 = 0,012 кг /1,9926482×10 –26 кг= 6,0221367×10 23.
= 0,012 кг /1,9926482×10 –26 кг= 6,0221367×10 23.
Этому числу частиц было присвоено наименование «число Авогадро» в честь итальянского физика Амедео Авогадро (1776 – 1856), сформулировавшего в 1811 г. закон (закон Авогадро), согласно которому в равных объёмах различных газов при одинаковых условиях содержится одинаковое количество молекул. Несмотря на то, что Авогадро ввёл новое для науки понятие «молекула» (от греч. – массочка) в 1811 году, только на химическом конгрессе 1860 года была принята резолюция, закрепляющая различные понятия атома и молекулы.
Порция вещества, характеризуемая числом частиц
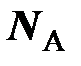 = 6,0221367×10 23, названа молем (моль), а физическая величина, характеризующая запас (количество) вещества в таких укрупнённых порциях, – количеством вещества
= 6,0221367×10 23, названа молем (моль), а физическая величина, характеризующая запас (количество) вещества в таких укрупнённых порциях, – количеством вещества 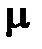 , единичное значение которого
, единичное значение которого 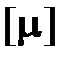 так же названо молем.
так же названо молем.
Числовое значение количества вещества 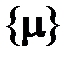 есть не что иное, как относительное число частиц – число укрупнённых порций частиц (молей), содержащихся в данном теле:
есть не что иное, как относительное число частиц – число укрупнённых порций частиц (молей), содержащихся в данном теле:
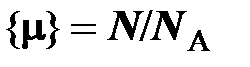 (2.5)
(2.5)
Именно так и следует пояснять смысл этой величины.
Если в уравнении (2.5) числовое значение количества вещества в соответствии с выражением (1.17) представить в виде 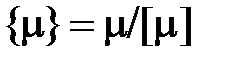 , то можно установить связь между числом частиц N и количеством вещества
, то можно установить связь между числом частиц N и количеством вещества 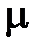 :
:
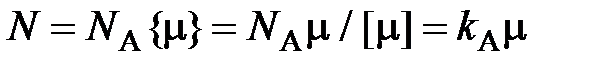 , (2.6)
, (2.6)
где 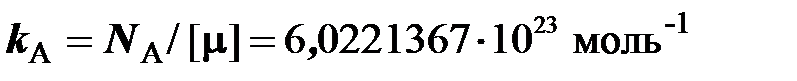 – постоянная Авогадро, равная отношению числа Авогадро
– постоянная Авогадро, равная отношению числа Авогадро 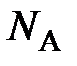 к единице количества вещества
к единице количества вещества 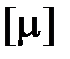 = 1 моль.
= 1 моль.
В настоящее время постоянную Авогадро обозначают символом N A, в основу которого положен символ N, используемый для обозначения числа частиц, что даёт основание, как это иногда встречается, постоянную Авогадро, имеющую единицу моль –1, называть числом Авогадро, не имеющим обозначения своей единицы. Чтобы избежать такой путаницы, постоянную Авогадро рекомендуется обозначать символом k A (по аналогии с обозначением постоянной Больцмана k Б), а число Авогадро – N A
Исходя из (2.6), получаем следующее уравнение связи для количества вещества
 ;
; 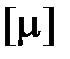 = 1 моль.
= 1 моль.
Следовательно, количество вещества – физическая величина, характеризующая количество частиц (структурных единиц, элементов) системы в укрупнённых порциях этих частиц – молях.
Единицей количества вещества является моль – одна из основных единиц СИ, – определяемый как количество вещества системы, содержащей столько же структурных элементов(такую порцию частиц), сколько содержится атомов в изотопе углерода 12С массой 0,012 кг.
Молярная масса. Отношение массы вещества к количеству вещества (молярности) называется молярной массой
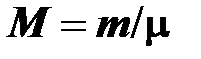 , [
, [ 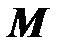 ] = 1 кг/моль. (2.7)
] = 1 кг/моль. (2.7)
Рекомендуемые дольные единицы молярной массы – г/моль и кг/кмоль.
Значение молярной массы вещества, выраженной в г/моль или кг/кмоль, числено равно относительной молекулярной массе вещества, определяемой по таблице Д. И. Менделеева: 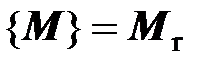 . Например,
. Например, 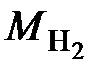 = 2,0158 г/моль = 2,0158 кг/кмоль. В связи с этим молярную массу на практике чаще всего выражают в г/моль или кг/кмоль. Не следует отождествлять молярную массу и относительную молекулярную массу, так как последняя является величиной безразмерной, отличающейся по физическому смыслу от молярной массы.
= 2,0158 г/моль = 2,0158 кг/кмоль. В связи с этим молярную массу на практике чаще всего выражают в г/моль или кг/кмоль. Не следует отождествлять молярную массу и относительную молекулярную массу, так как последняя является величиной безразмерной, отличающейся по физическому смыслу от молярной массы.
Mолярная масса численно равна массе молекул, число которых равно числу Авогадро,  , если в качестве единицы молярной массы берётся 1 кг/кмоль или 1 г/моль.
, если в качестве единицы молярной массы берётся 1 кг/кмоль или 1 г/моль.
Молярный объём. Отношение объёма однородного вещества к количеству вещества (молярности) называется молярным объёмом
 ,
, 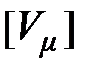 = 1 м3/моль. (2.8)
= 1 м3/моль. (2.8)
Кубический метр на моль равен молярному объёму вещества, занимающего при количестве вещества 1 моль объём 1 м 3.
Молярный объём разрежённого газа при нормальных физических условиях (НФУ): 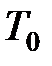 = 273,15 K (0o C) и
= 273,15 K (0o C) и 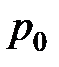 = 101 325 Па равен (по данным на 1986 год)
= 101 325 Па равен (по данным на 1986 год)
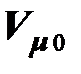 = 22,4141×10 –3 м 3/моль = 22,4141 м 3 / кмоль.
= 22,4141×10 –3 м 3/моль = 22,4141 м 3 / кмоль.
Газовые постоянные. Путём объединения (обобщения) газовых законов Гей-Люссака и Бойля–Мариотта можно получить следующее соотношение
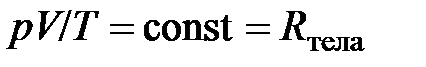 ; [
; [ 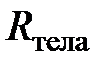 ] = 1 Дж/К, (2.9)
] = 1 Дж/К, (2.9)
из которого следует, что для данного количества (данной массы) разрежённого газа отношение произведения давления на объём к термодинамической температуре есть величина постоянная. Эту постоянную величину, поскольку она относится ко всему телу (системе), назовём газовой постоянной тела (газообразного тела)и обозначим 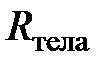 .
.
Удельная газовая постоянная. Отношение газовой постоянной тела к массе газа называется удельной газовой постоянной
 , [
, [ 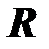 ] = 1 Дж/(кг×К).(2.10)
] = 1 Дж/(кг×К).(2.10)
Молярная (универсальная) газовая постоянная. Отношение газовой постоянной тела к количеству вещества (молярности) газа называется молярной газовой постоянной
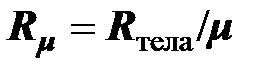 , [
, [ 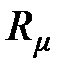 ] = 1 Дж/(моль×К). (2.11)
] = 1 Дж/(моль×К). (2.11)
Решая совместно уравнения (2.8), (2.9) и (2.11), можно выразить молярную газовую постоянную через параметры состояния и вычислить её значение по соответствующим значениям параметров состояния, например, для значений параметров состояния при нормальных физических условиях (по данным на 1986 г)
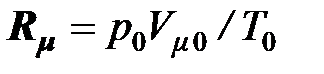 = 101 325 × 22,4141×10–3/273,15 =
= 101 325 × 22,4141×10–3/273,15 =
= 8,314 51Дж/(моль×К) = 8314,51Дж/(кмоль×К).
Поскольку молярный объём  при нормальных физических условиях для всех разрежённых газов имеет одинаковое значение, то и молярная газовая постоянная
при нормальных физических условиях для всех разрежённых газов имеет одинаковое значение, то и молярная газовая постоянная  для всех газов также имеет одинаковое значение. Это дало основание называть эту газовую постоянную универсальной газовой постоянной. Однако этот термин не соответствует уравнению связи (2.11) для молярной газовой постоянной и поэтому считается устаревшим.
для всех газов также имеет одинаковое значение. Это дало основание называть эту газовую постоянную универсальной газовой постоянной. Однако этот термин не соответствует уравнению связи (2.11) для молярной газовой постоянной и поэтому считается устаревшим.
Решая совместно уравнения (2.7), (2.10) и (2.11), можно установить связь между удельной газовой постоянной и молярной газовой постоянной
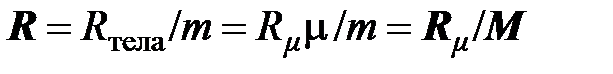 . (2.12)
. (2.12)
Используя это соотношение, определим в качестве примера удельную газовую постоянную водорода (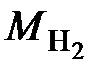 = 2,0158×10 –3 кг/моль)
= 2,0158×10 –3 кг/моль)
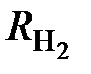 = 8,31451/2,0158×10 –3 = 4124,670 Дж/(кг×К).
= 8,31451/2,0158×10 –3 = 4124,670 Дж/(кг×К).
Отношение газовой постоянной тела к числу молекул газа можно назвать молекулярной газовой постоянной
 ,[RN] = 1 Дж/К. (2.13)
,[RN] = 1 Дж/К. (2.13)
Молекулярная газовая постоянная определяет «долю» газовой постоянной тела, приходящуюся на одну молекулу.
Если 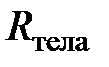 выразить с помощью (2.11) через молярную газовую постоянную, то с учётом (2.6) получим
выразить с помощью (2.11) через молярную газовую постоянную, то с учётом (2.6) получим
 . (2.14)
. (2.14)
Отношение двух констант даёт новую константу, которую принято называть постоянной Больцмана
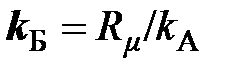 = 8,31451/6,0221367×10 23 = 1,380658×10 –23 Дж/К.
= 8,31451/6,0221367×10 23 = 1,380658×10 –23 Дж/К.
Следовательно, в соответствии с выражением (2.14), постоянная Больцмана есть не что иное, как молекулярная газовая постоянная, определяемая отношением газовой постоянной тела к числу молекул газа (2.13).
Разновидности записи уравнения состояния идеального газа. Уравнение, выражающее связь между параметрами равновесного состояния термодинамической системы или локально равновесных её частей, 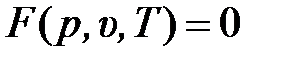 называется уравнением состояния.
называется уравнением состояния.
В связи с данным определением уравнение (2.9) 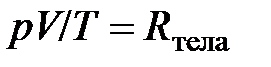 является уравнением состояния идеального газа. С учётом введённых газовых постоянных это уравнение можно записать в следующих видах:
является уравнением состояния идеального газа. С учётом введённых газовых постоянных это уравнение можно записать в следующих видах:
¨ через удельную газовую постоянную 
– для газа объёмом 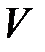
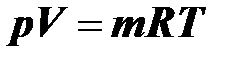 , (2.15)
, (2.15)
– для удельного объёма 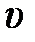
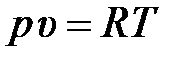
– и для плотности 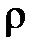
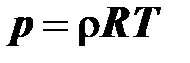 ; (2.16)
; (2.16)
¨¨ через молярную газовую постоянную 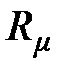
– для газа массой 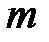
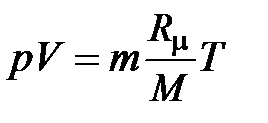 (2.17)
(2.17)
– для количества вещества (молярности) 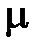
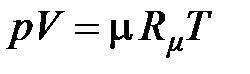
– для молярного объёма 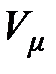
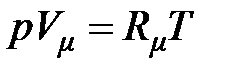 ;(2.18)
;(2.18)
Удельная газовая постоянная для смеси газов находится по формуле
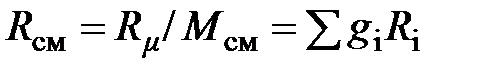 , (2.19)
, (2.19)
где 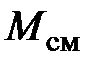 – молярная масса смеси, равная
– молярная масса смеси, равная
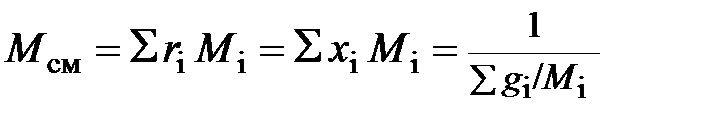 . (2.20)
. (2.20)
Здесь 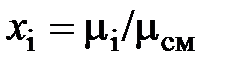 – молярная доля
– молярная доля 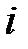 -го компонента смеси, равная в случае идеального газа объёмной доле
-го компонента смеси, равная в случае идеального газа объёмной доле 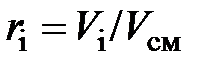 ;
;
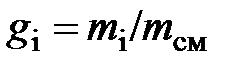 – массовая доля
– массовая доля 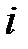 -го компонента смеси.
-го компонента смеси.
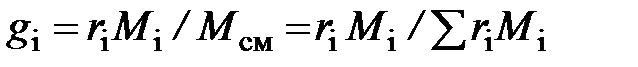 .
.
Плотностью компонента смеси называется отношение массы компонента смеси к его объёму (парциальному объёму)
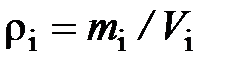 . (2.21)
. (2.21)
Парциальной плотностью, или массовой концентрацией компонента смеси называется отношение массы компонента смеси к объёму смеси
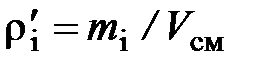 (2.22)
(2.22)
В таблице 3 приведён химический состав атмосфер Земли, Венеры и Марса.
Таблица 3 – Химический состав атмосфер Земли, Венеры и Марса
| Газ | Молярная масса 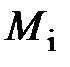 ,
кг/кмоль ,
кг/кмоль
| Массовый состав 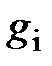 сухого воздуха Земли сухого воздуха Земли
| Объёмный состав 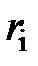 , % атмосферы , % атмосферы
| |||
| Земли | Венеры | Марса | ||||
| Азот N2 | 28,0134 | 0,7553 | 78,03 | 3,5 | 2,5¸2,7 | |
| Кислород O2 | 31,9982 | 0,2314 | 20,99 | < 10 - 3 | 0,1¸0,15 | |
| Аргон Ar | 39,948 | 0,0128 | 0,94 | 0,0015 | 1,5¸1,6 | |
| Диоксид углерода CO2 | 44,0098 | 0,0005 | 0,03 | 96,5 | ||
| Водород H2 | 2,0158 | < 5×10 - 5 | < 5×10 - 5 | < 10 - 3 | – | |
Date: 2015-05-08; view: 1658; Нарушение авторских прав