
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Своимчисловым значениемпоказывает, во сколько раз размерданногосвойства отличается от размераэтого свойства, принятогоза единицу сравнения
|
|
Все перечисленные атрибуты физической величины можно
наглядно представить в виде формулы
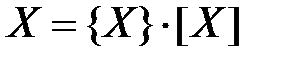 , (1.17)
, (1.17)
где 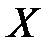 – значение конкретной физической величины;
– значение конкретной физической величины;
{ 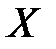 } – числовое значение физической величины(отвлечённое число) в принятой единице (число единичных порций свойства в данном размере свойства);
} – числовое значение физической величины(отвлечённое число) в принятой единице (число единичных порций свойства в данном размере свойства);
[ 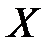 ] – принятая единица физической величины.
] – принятая единица физической величины.
Например, в выражении для давления 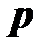 = 101 кПа, 101 – отвлечённое число, представляющее числовое значение давления: {
= 101 кПа, 101 – отвлечённое число, представляющее числовое значение давления: { 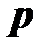 } = 101;
} = 101;
кПа – принятая в данном случае единица давления (вернее, обозначение единицы давления – килопаскаля): [ 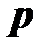 ]= 1 кПа;
]= 1 кПа;
101 кПа – значение давления.
Как размер (количество) свойства не зависит от размера этого свойства, выбранного в качестве единицы сравнения, так и значение ФВ, не зависит от значения выбранной единицы ФВ. Ещё раз подчеркнём, что нет размера ФВ, но есть значение ФВ. Размер имеют каксамо измеряемое свойство таки порция этого свойства, принятая за единицу сравнения, – мера свойства.
1.3.3 Размерность физических величин. В большинстве случаев при рассмотрении физических величин знание их размерности не требуется, т. к. достаточно знать единицу этой величины и её связь с единицами основных величин (метод размерностей находит применение, например, в теории подобия при определении чисел подобия, когда уравнения исследуемых процессов неизвестны). В то же время в литературе широко укоренились утверждения (ошибочные) типа: «размерность скорости – метр в секунду», «моль – размерность количества вещества» и т. п. Ошибочность утверждений такого типа обусловлена отождествлением единицы физической величины и её обозначения с размерностью, а также тем, что раньше квадратные скобки [ 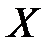 ], содержащие обозначение величины
], содержащие обозначение величины 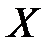 , означали размерность величины, а теперь означают единицу физической величины (а не размерность). Сейчас принята такая запись [ p ] = 1 Па, которая читается так: «Единица давления равна паскалю». Неправильно заключать в квадратные скобки единицу величины, например, [Па], хотя такая запись встречается часто.
, означали размерность величины, а теперь означают единицу физической величины (а не размерность). Сейчас принята такая запись [ p ] = 1 Па, которая читается так: «Единица давления равна паскалю». Неправильно заключать в квадратные скобки единицу величины, например, [Па], хотя такая запись встречается часто.
Символическое выражение производной (вторичной) величины через основные (первичные) называется размерностью физической величины. Она отражает связь данной величины с величинами, принятыми за основные в рассматриваемой системе величин.
Так, система величин, которая определяется Международной системой единиц SI (в русской транскрипции СИ – система интернациональная; СИ читается раздельно: «эс-и», а не слитно «си»), содержит семь основных системных величин 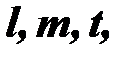
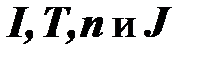 , где
, где 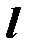 – длина,
– длина, 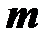 – масса,
– масса, 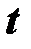 – время,
– время, 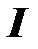 – сила электрического тока,
– сила электрического тока, 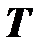 – термодинамическая температура,
– термодинамическая температура,  – количество вещества,
– количество вещества,  – сила света. Для этих величин условно приняты следующие размерности: для длины – L, массы – M, времени – T, силы электрического тока – I, термодинамической температуры –
– сила света. Для этих величин условно приняты следующие размерности: для длины – L, массы – M, времени – T, силы электрического тока – I, термодинамической температуры –  , количества вещества – N и силы света J. Размерности записываются прописными буквами и печатаются прямым шрифтом.
, количества вещества – N и силы света J. Размерности записываются прописными буквами и печатаются прямым шрифтом.
Над размерными величинами, как и над самими величинами, можно производить действия умножения, деления, возведения в степень и извлечения корня. Показатель степени, в которую возведена размерность основной величины, входящей в степенной одночлен, называют показателем размерности.
Размерность величины 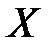 обозначается так:
обозначается так:
dim 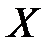 (англ. dimension – размерность). Например, размерности силы
(англ. dimension – размерность). Например, размерности силы  и работы:
и работы: 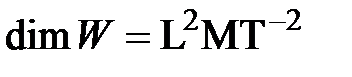 .
.
Различают размерные и безразмерные величины. Размерной физической величинойназывают такую величину, в размерности которой хотя бы один из показателей размерности не равен нулю. Безразмерной физической величиной называют физическую величину, в размерности которой все показатели размерности равны нулю, а размерность равна единице. Например, размерность относительной плотности (она равна отношению плотности данного вещества к плотности образцового вещества) равна 1 (единице). Поэтому не следует допускать ошибок при установлении размерности безразмерных относительных величин: их размерности равны 1 (единице), а не 0 (нулю), как нередко ошибочно пишут. Необходимо использовать понятие «размерность физической величины», а не понятие «размерность единицы физической величины».
Следует строго различать следующие понятия: обозначение физической величины, размерность физической величины, единица физической величины, обозначение единицы физической величины. Разграничение этих понятий наглядно представлено в виде таблицы 1.
Таблица 1 – Атрибуты физической величины
| Физическая величина (наименование величины) | Обозначение физической величины | Размерность физической величины | Наименование единицы физической величины | Единица физической величины |
| Скорость | с | 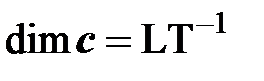
| метр в секунду | [ с ] = 1 м/с |
1.3.4 Определения физических величин в соответствии с уравнениями связи. Определения физических величин должны находиться в строгом соответствии с уравнениями связи между величинами, из которых их выводят. Уравнениями связи между физическими величинами являются уравнения, в которых под буквенными символами понимаются физические величины. Определения физических величин в соответствии с уравнениями связи формулируются так:
1) плотность однородного вещества – физическая величина, равная отношению массы вещества к его объёму: 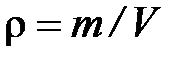 ;
;
2) удельная теплоёмкость – физическая величина, равная отношению теплоёмкости всего тела (вещества) к его массе: 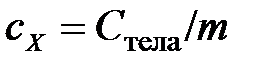 .
.
В связи с тем, что физическая величина – первичное понятие, а единица физической величины – вторичное понятие и физическая величина не зависит от единиц, в которых её выражают, неприемлемы такие определения физических величин, которые содержат единицы или обозначения физических величин, например:
1) плотность однородного тела – это масса единицы объёма (1 м3), или масса тела, отнесённая к единице объёма.
Оба эти утверждения неправильны. Плотность это вовсе не масса, а физическая величина другой природы с размерностью массы, делённой на объём. Сказать, что плотность – это масса (единицы объёма), значит сказать, что хвост – это животное (без головы и туловища). Плотность не является также массой, отнесенной к единице объёма, т. е. 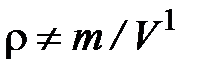 , где
, где 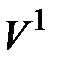 =
=
= 1 м3 – единичный объём (СИ). Кроме того, термины «единица объёма», «единичный объём» неоднозначны, поскольку любой объём (1 л, 1 см 3,
1 м 3 и т. д.), может быть принят в качестве единичного объёма, а физическая величина, как уже отмечалось, не зависит от единиц, в которых её выражают;
2) удельной теплоёмкостью вещества 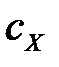 называют величину, равную количеству теплоты (тепла)
называют величину, равную количеству теплоты (тепла) 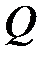 , которое необходимо сообщить 1 кг вещества, чтобы увеличить его температуру на 1 о С.
, которое необходимо сообщить 1 кг вещества, чтобы увеличить его температуру на 1 о С.
Во-первых, удельная теплоёмкость не может равняться теплоте (это разные физические величины); во-вторых, определение физической величины не зависит от единиц, в которых выражены величины; в-третьих, введение в определение обозначений величин усложнило его.
Однако, кроме определения величины, следующего из формулы связи между физическими величинами, полезно давать дополнительные пояснения, которые способствуют усвоению физического смысла величины. Например, «единицей плотности СИ является килограмм на кубический метр, равный плотности однородного вещества, масса которого при объёме 1 м3 равна 1 кг» или «числовое значение плотности равно числовому значению массы тела единичного объёма», т. е. плотность может равняться массе тела единичного объёма лишь численно. Например, нельзя говорить, что при единичном объёме плотность 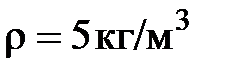 равна массе
равна массе 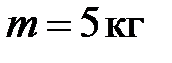 , но можно говорить, что числовое значение
, но можно говорить, что числовое значение 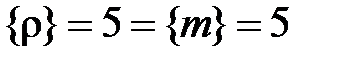 при единичном объёме
при единичном объёме 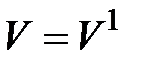 = 1 м3.
= 1 м3.
Аналогичным образом, теплоёмкость численно равна теплоте, которую нужно подвести к телу, чтобы изменить его температуру на один градус.
Расчётные формулы рекомендуется записывать в виде уравнений между физическими величинами, когда отсутствуют коэффициенты, зависящие от единиц, в которых выражены физические величины. При подстановке в такие формулы значений величин (вместо буквенных обозначений величин), выраженных в единицах СИ, результат будет получаться также в единицах СИ. При этом не потребуется затрачивать время на проверку правильности выбора единиц и на выяснение, в каких единицах выражены числовые коэффициенты и сам результат вычисления. Поэтому запись уравнения состояния идеального газа через числовые множители:
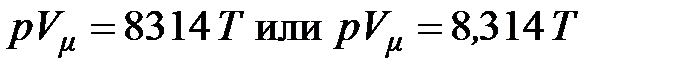 ,
,
как это иногда практикуется в курсах термодинамики, нельзя считать рациональной по трём причинам: во - первых, числовое значение величины не является полной характеристикой физической величины и, в отличие от значения физической величины, зависит от выбранной единицы; во-вторых, нарушается размерность левой и правой частей уравнения и,
в-третьих, числовое значение опытной величины, к которым следует отнести молярную газовую постоянную, в процессе повышения точности измерений всё время уточняется [например, 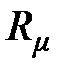 = 8314,51 Дж/(кмоль×К)], а значит постоянно нужно уточнять и запись уравнения состояния.
= 8314,51 Дж/(кмоль×К)], а значит постоянно нужно уточнять и запись уравнения состояния.
1.3.5 О наименовании физических величин. Первоначально наименование физических величин осуществлялось по схеме: «количество свойства» или «величина свойства». Например, «количество вещества», «количество движения», «количество теплоты (тепла)», «величина массы», «величина энергии» и др. Данные словосочетания имеют смысл, если под словом «величина» понимать количество, размер свойства, наименование которого следует за словом «величина». Например, «величина массы» дословно должно означать «количество» свойства, именуемого словом «масса», «количество теплоты» - «количество свойства», именуемого словом «теплота».
Постепенно стали применяться сокращенные наименования физических величин, названия которых зачастую совпадали с названиями свойств. Например, под массой стали понимать в первую очередь не свойство тела (инертность), а физическую величину, характеризующую это свойство с количественной стороны. Поэтому стали критиковаться выражения типа «на нити висит масса 5 кг», «элементарный объем вошёл через клапан», «энергия превращается», «заряд перемещается» и т. п. Рекомендуется разделять названия физических величин и физических свойств, например,
записывая приведённые выше выражения так: «на нити висит тело массой
5 кг», «элемент среды объёмом 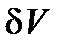 входит через клапан», «движение изменяет свою форму, или вид», «заряженные частицы перемещаются» и т. п. С этой же целью для вновь вводимых величин стали использовать названия, не совпадающие с названиями физических свойств, например, «энтальпия», «энтропия», «эксергия» (уже никому в голову не придёт мысль сказать, что «энтропия превратилась в энтальпию», т. к. всем ясно, что это – физические величины, а они превращаться ни во что не могут).
входит через клапан», «движение изменяет свою форму, или вид», «заряженные частицы перемещаются» и т. п. С этой же целью для вновь вводимых величин стали использовать названия, не совпадающие с названиями физических свойств, например, «энтальпия», «энтропия», «эксергия» (уже никому в голову не придёт мысль сказать, что «энтропия превратилась в энтальпию», т. к. всем ясно, что это – физические величины, а они превращаться ни во что не могут).
В настоящее время не рекомендуется применять термины «величина» (в смысле количества) и «количество» для выражения количественной стороны рассматриваемого свойства, характеризуемой понятием «физическая величина». Например, писать «величина массы», «величина длины», «количество энергии», «количество теплоты» и т. п., так как эти словосочетания двусмысленны из-за многозначности терминов «величина», «масса», «длина», «энергия», «теплота», означающих и физическую величину ( числовую характеристику свойства), и само свойство.
Если под терминами «масса», «энергия», «теплота» и др. понимать физические величины, то использование слов «величина» и «количество» перед наименованием физической величины приводит к тавтологии («величина величины» или «количество количества»), кроме того, физическая величина не имеет размера и, следовательно, нельзя говорить об её количестве (например, термин «количество теплоты» можно понять как количество физической величины «теплота»). В приведённых примерах слово «величина» следует по возможности опускать как излишнее; в отдельных случаях его можно заменить термином «значение», например, «значение массы».
Более того, некоторые свойства оказались столь общими, многогранными (например, «вещество» и «движение»), что для количественной характеристики отдельных сторон этих свойств стали использовать различные величины. В результате использование общих терминов «количество движения» и «количество вещества» для наименования только одной из ФВ, характеризующих эти свойства, оказалось нецелесообразным.
Например, первоначально термин «количество движения» использовался для наименования векторной физической величины, получаемой как произведение массы на вектор скорости: 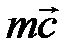 . В последствии выяснилось, что эту векторную величину нельзя использовать для оценки запаса (количества) хаотического движения в телах. Для этой цели стала использоваться новая физическая величина «энергия». Следовательно, для характеристики запаса (количества) движения в системе стали использовать две различные величины и, чтобы не использовать общий термин «количество движения» для величины
. В последствии выяснилось, что эту векторную величину нельзя использовать для оценки запаса (количества) хаотического движения в телах. Для этой цели стала использоваться новая физическая величина «энергия». Следовательно, для характеристики запаса (количества) движения в системе стали использовать две различные величины и, чтобы не использовать общий термин «количество движения» для величины 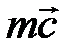 , её стали называть «импульсом».
, её стали называть «импульсом».
Итак, в настоящее время общая количественная характеристика движения «количество движения» стала включать в себя несколько количественных характеристик (физических величин): импульс, энергию, момент импульса и др. Следовательно, под количеством движения КД следует понимать обобщающую величину: КД { Е, 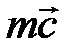 ,
, 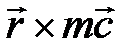 и др.}.
и др.}.
Аналогичным образом, оказалось, что для характеристики запаса (размера, количества) вещества (материи) в системе могут использоваться различные количественных характеристики (физические величины): масса, число частиц, объём, вес. Поэтому использование общего термина «количество вещества» для наименования одной из величин 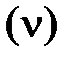 , характеризующей запас (количество) вещества через порцию частиц (моль) нецелесообразно. Однако до настоящего времени эту величину так и не переименовали (по соображениям, изложенным в разделе 1.4.2, данную величину рекомендуется назвать «молярность вещества», или коротко «молярность»). По аналогии с количество движения количество вещества (материи) КВ (КМ) следует рассматривать в качестве обобщающей величины: КВ { m, V, N,
, характеризующей запас (количество) вещества через порцию частиц (моль) нецелесообразно. Однако до настоящего времени эту величину так и не переименовали (по соображениям, изложенным в разделе 1.4.2, данную величину рекомендуется назвать «молярность вещества», или коротко «молярность»). По аналогии с количество движения количество вещества (материи) КВ (КМ) следует рассматривать в качестве обобщающей величины: КВ { m, V, N, 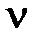 и др.}.
и др.}.
Итак, в настоящее время для наименования физических величин используются только два составных термина: «количество вещества» и «количество теплоты». В последнем термине слово «теплота» должно означать наименование свойства – хаотического движения. Однако термин «теплота» часто используется, даже в одних и тех же учебниках, в качестве сокращенного наименования той же физической величины, т. е. термины «теплота» и «количество теплоты» рассматриваются как синонимы. В результате возникает путаница с категориями. Поэтому целесообразно для сокращенного наименования хаотического движения использовать термин «тепло» (например, «перенос тепла»), а для наименования ФВ использовать термины «теплота», или «количество тепла» – количество хаотического движения (последнее менее предпочтительно, т. к. оно составное ).
Для каждой физической величины, как правило, допускается применение только одного наименования. Допускается использовать, кроме основных наименований физических величин, их краткую (так называемую усечённую) форму при непременном условии, что это не вызовет каких-либо недоразумений, например, «линейная скорость» и «скорость»; «поверхностная плотность теплового потока» и «плотность теплового потока».
Для производных величин, получаемых от деления какой-либо величины на массу тела, следует дополнительно применять прилагательное «удельный»; при отношении к объёму – «пространственный», или «объёмный»; при отношении к количеству вещества – «молярный», но не «мольный» и не «молекулярный»; при отношении к числу частиц – «молекулярный»; при отношении к длине – «линейный»; при отношении к площади поверхности – «поверхностный».
Примеры: «удельная теплоёмкость» (а не «массовая теплоёмкость»), Дж/(кг×К); «удельная теплота парообразования воды» (сокращённо «теплота парообразования»), кДж/кг; «объёмная энергия», Дж/м3; «объёмный вес» (а не «удельный вес», как общепринято), Н/м3; «молярная газовая постоянная» (а не молекулярная), Дж/(моль.К).
Во избежание многозначности терминов, получаемых с применением прилагательных «объёмный» и «поверхностный» и используемых как для разграничения наименований разновидностей одной и той же величины (например, в гидромеханике рассматриваются поверхностные силы, действующие на поверхности выделенного элемента жидкости и объёмные силы, действующие по всему объёму элемента жидкости), так и для наименования производных величин, следует при образовании терминов производных величин после соответствующих прилагательных добавлять слово «плотность ». Например, «поверхностная плотность потока энергии», «объёмная плотность потока энергии».
Не следует использовать устаревшие наименования физических величин, даже если они встречаются в литературе. Например, следует использовать термины вместимость сосуда, а не ёмкость сосуда; динамическая вязкость, а не коэффициент динамической вязкости; теплопроводность материала, а не коэффициент теплопроводности; количество вещества, а не число молей; молярная масса, а не мольная или молекулярная масса; массовый или объёмный расход, а не весовой, часовой или секундный расход; энтальпия, а не теплосодержание, чёрное тело, а не абсолютно чёрное тело, теплота сгорания топлива, а не теплотворность топлива и др. Примеры использования современных терминов теплотехнических величин приведены в приложении Б.
Date: 2015-05-08; view: 1020; Нарушение авторских прав