Латинский алфавит

A	– площадь	P	– мощность
с	– скорость	p	– давление
d	– диаметр	Q	– теплота
E	– энергия	r	– радиус
F	– сила	s	– путь
g	– ускорение свободного падения	S	– энтропия
H	– энтальпия	t	– время
I	– сила электрического тока	T	– температура
K	– импульс	U	– электрическое напряжение
l	– длина	V	– объём
m	– масса		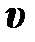– удельный объём
M	– молярная масса	W	– работа
N	– число (частиц, молекул, импульсов, оборотов и т. п.)	w	– удельная работа

Греческий алфавит

	– коэффициент полезного действия		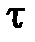– касательное напряжение
	– электрический заряд	F	– энергетический поток (поток энергии), Вт (тепловой, световой, звуковой)
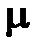
	– количество вещества (молярность)		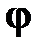– поверхностная плотность энергетического потока (теплового потока), Вт/м2
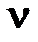
	– частота		– угол (плоский)
P	– период		– телесный угол
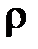
	– плотность		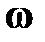– угловая скорость
	– нормальное напряжение		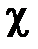– химический потенциал

Приведённые символы основных величин предлагается стандартизировать и использовать во всех дисциплинах, начиная со школьных курсов (число этих величин и их обозначения могут уточняться по решению соответствующих комиссий).

Ещё раз подчеркнём, что в отличие от общепринятых обозначений соответствующих величин, когда каждая величина имеет несколько синонимичных обозначений, в предлагаемом стандарте основных величин каждая величина имеет одно единственное обозначение, которое должно неукоснительно использоваться во всех дисциплинах. В этой связи совершенно недопустимо использовать символ одной основной величины для обозначения другой основной величины, например, для массы использовать символ молярной массы M, для обозначения работы использовать символ площади A, для обозначения импульса – символ давления p и т. п. В то же время за каждым из этих символов сохраняется многозначность, т. е. они могут использоваться для обозначения не только основных величин, но и других величин, не входящих в таблицу основных величин. Например, буквой U можно обозначать не только электрическое напряжение, но и внутреннюю энергию; буквой M не только молярную массу, но и момент силы и т. п.

1.4.3 Использование индексации при обозначении однородных величин. Расчленение общего понятия на частные может быть достигнуто применением:

1) самостоятельных буквенных обозначений в специальных дисциплинах, например, при обозначении составляющих сил (F, P, Q, R, G) в теоретической механике;

2) индексации, т. е. применения индексов у одних и тех же буквенных обозначений в общих дисциплинах, таких как физика, например, для обозначения различных видов энергии E: 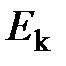–для кинетической энергии, 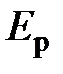– для потенциальной энергии. В этой связи нерационально загружать память обучаемого требованием запомнить, что в одном разделе курса физики буква 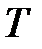используется для обозначения кинетической энергии, а в других разделах – для обозначения температуры и периода колебаний. Следовательно, применение индексации позволяет использовать одну и ту же букву для различных видов одной и той же величины и тем самым уменьшить многозначность букв, используемых для обозначения разнородных величин (в теоретической механике массу тела и момент силы принято обозначать одинаковым символом M, что создаёт большие трудности при изучении этой дисциплины (некоторые авторы даже вынуждены момент силы обозначать символом 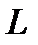, что также нерационально); рационально массу тела обозначать символом , а для обозначения "массы точки" использовать индексацию, например, ).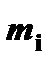

Индексы имеют уменьшенный размер символов и, как правило, располагаются справа внизу у основания буквенного обозначения величины; при этом не рекомендуется использовать для индекса более трёх букв. Буквы, используемые в индексах, печатают прямым шрифтом.

Некоторые индексы физических величин имеют специальное значение. Например, звёздочка служит для обозначения параметров заторможенного потока: 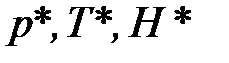; знак нуля – для обозначения стандартных состояний: ,или 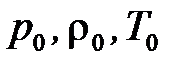; буква «о» – для указания на обратимость процесса: 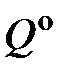, 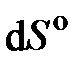и др.

Обозначения величин должны быть наглядными и связанными с терминами этих величин, что весьма важно для запоминания и понимания величин. Например: 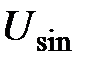– синусоидальное напряжение, 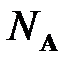– число Авогадро; 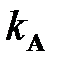– постоянная Авогадро, моль ^–1; 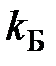– постоянная Больцмана и др.

Использование индексации буквенных обозначений величин позволяет не только использовать одну и ту же букву для обозначения различных видов какой-либо величины (и тем самым облегчить их запоминание), но и даже освободить эту букву для обозначения совершенно других величин. Так, введение символа 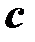для скорости в теплотехнике затруднялось тем, что этой буквой в теплотехнике принято обозначать удельную теплоёмкость произвольного процесса. Однако на практике наиболее часто используются изобарная 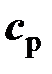и изохорная 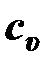теплоёмкости, обозначения которых нельзя спутать с обозначением скорости 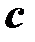. Введение индексов 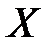для изопроцессов ( 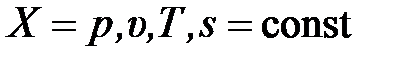и 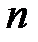для политропного процесса позволяет ввести обозначения теплоёмкостей произвольного изопроцесса 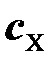и политропного процесса 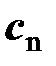. Всё это позволяет освободить букву 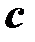для обозначения скорости потока, а букву 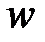, используемую в теплотехнике для обозначения скорости потока, – для обозначения удельной работы, что обеспечит преемственность обозначений величин в теплотехнике, физике (физике ради своих обширных приложений – гидромеханики и теплотехники – следует пойти на уступки и ввести для обозначения скорости вместо символа 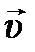символ 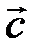, а вместо символа импульса 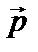символ 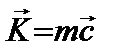) и механике.

1.4.4 Производные обозначения разнородных величин. Производное обозначение физической величины – это обозначение производной физической величины, состоящее из буквенных обозначений основных величин, входящих в определяющее эту величину уравнение. В качестве основного символа производной величины берётся символ величины, стоящей в числителе определяющего уравнения, а обозначения величин, стоящих в знаменателе, записывается в виде нижнего индекса курсивом (с наклоном, как и символ основной величины).

Примерами производных обозначений величин являются обозначения массового расхода: 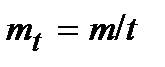, кг/с; объёмного расхода: 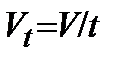, м³/с; молярной теплоёмкости изобарного процесса: 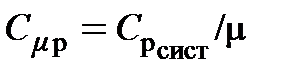, Дж/(моль×К) и др. Для сравнения приведём обозначения индексированных величин, например, массы протона 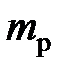и теоретической скорости 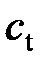,у которых индексы записаны без наклона.

Обозначения производных величин весьма наглядны и легко запоминаемы, позволяют просто определять единицы этих величин и сами формулы, определяющие эти величины, – по виду самого символа. Для этого надо знать основное правило написания уравнения связи по виду производного обозначения величины: буквенное обозначение основного символа необходимо ставить в числитель, а обозначение индекса – в знаменатель уравнения связи. Так, например, единица массового расхода, согласно символу 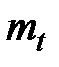: = 1кг/с.

Для обозначения производных величин, получаемых от деления какой-либо величины на время, всё чаще используется применение точки над символом величины, стоящей в числителе. Например, для массового расхода 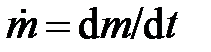и объёмного расхода .

Производные обозначения физических величин всё чаще применяются в технической и учебной литературе. Однако такое обозначение величин ещё не нашло широкого и обоснованного применения во всех дисциплинах, начиная со школьных курсов физики. Например, сейчас молярный объём, как уже отмечалось, обозначается символом 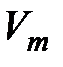, что противоречит производному обозначению величин, согласно которому 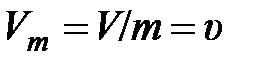– удельный объём. Правильное производное обозначение молярного объёма: 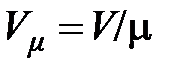, где 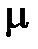– количество вещества (молярность). Последнее ещё раз указывает на необходимость обозначения количества вещества (молярности) символом .

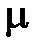Если в теории формула (уравнение) используется редко (однократно), то нет смысла вводить специальные буквенные обозначения для величин, входящих в эту формулу, а лучше для обозначения этих величин использовать производные обозначения, устраняющие многозначность отдельных букв. Усложнение символа в отдельной формуле с лихвой окупается понятностью величин, входящих в эту формулу, без дополнительных разъяснений символов. Например, в термодинамике уравнение, связывающее давление идеального газа с кинетической энергией хаотического движения молекул и их концентрацией n, даётся всего один раз. Поэтому нет надобности для написания этого уравнения вводить специальное обозначение концентрации молекул n (так как этой буквой в термодинамике принято обозначать показатель политропного процесса), а лучше использовать производное обозначение концентрации частиц : .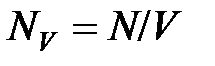

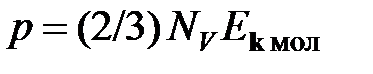Если основная величина ЕСБОВ в специальной дисциплине встречается редко и её символ использован для обозначения какой-либо специальной величины, то в случае возникшей необходимости использовать основную величину, у которой был использован символ для обозначения специальной величины, для её обозначения целесообразно использовать производное обозначение, а не вводить многозначное буквенное обозначение. Например, в электротехнике буквой 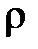обозначается объёмная плотность заряда. Поэтому при расчёте массы, например проводника, для
обозначения его плотности следует использовать производное обозначение : .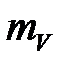

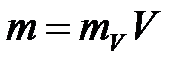Усложнение буквенных обозначений величин (в разумных пределах) путём использования производных обозначений в соответствии с уравнениями связи целесообразнее применения синонимичных буквенных обозначений в общетехнических дисциплинах, где данная величина не является главной (основной). Применение производных обозначений позволяет уменьшить многозначность символов, применяемых в общих курсах, и тем самым делает возможным создание таблиц однозначных символов величин и уравнений связи для них, даваемых в приложениях этих курсов. Таблица обозначений величин лабораторного практикума, построенная по такому принципу, приводится в приложении В (полная таблица теплотехнических величин дана в работе [9].

В заключение отметим, что, хотя идеальную систему буквенных обозначений величин, удовлетворяющую в должной мере всем дисциплинам, создать невозможно, улучшение ЕСБОВ всегда возможно, и оно будет непрерывно происходить по мере развития науки и техники и появления всё новых и новых величин.

Date: 2015-05-08; view: 1143; Нарушение авторских прав