Сутність та формулювання першого закону термодинаміки

Перший закон термодинаміки є кількісним формулюванням закону збереження енергії в застосуванні до процесів, що пов'язані з перетворенням теплоти в роботу. Ще в працях М.Ломоносова (1748р.) дане загальне положення принципу збереження руху (енергії), що безпосередньо зв'язано зі змістом першого закону термодинаміки. В обгрунтуванні закону важливу роль відіграли праці Гесса, Майера, Джоуля, Гельмгольца та інших видатних вчених.

Існує декілька формулювань першого закону термодинаміки. Основними з них є такі:

- енергія ізольованої системи стала;

- різні форми енергії переходять одна в іншу в строго еквівалентних співвідношеннях;

- неможливо створити вічний двигун (perpetum modile) першого роду, який давав би можливість одержувати роботу, не витрачаючи на це енергії.

Як узагальнення всіх формулювань першого закону термодинаміки виступає рівняння

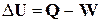, (1.1)

яке є наслідком сталості запасу внутрішньої енергії ізольованої системи: в будь-якому процесі збільшення внутрішньої енергії системи (DU) дорівнює кількості теплоти (Q), що поглинається системою, мінус кількість роботи (W), яку виконала при цьому система.

В системі СІ за одиницю вимірювання теплоти, роботи і внутрішньої енергії беруть джоуль (Дж). Інколи в фізико-хімічних розрахунках користуються калоріями (кал). Співвідношення між джоулем і калорією має вигляд: 1 кал = 4,184 Дж.

Розглянемо фізичний зміст величин рівняння (1.1).

U – внутрішня енергія системи. Це повний запас енергії нерухомої системи, на яку не діють зовнішні сили (тиск). Внутрішня енергія системи складається з енергії поступального та обертального руху молекул, енергії коливання атомів, енергії обертання електронів тощо.

Розглядаючи принцип еквівалентності теплоти і роботи, відкритий Джоулем (1840-1845), стосовно до кругового (циклічного) процесу, одержуємо

.

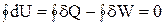З рівняння випливає, що величина dU є повним диференціалом внутрішньої енергії системи. Величина, диференціал якої є повним диференціалом змінних станів, називається функцією стану системи. Попередній вираз можна переписати у вигляді

.

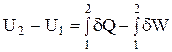Таким чином, внутрішня енергія системи є однозначною, безперервною і кінцевою функцією стану системи.

Розбиваючи інтеграл в попередньому рівнянні на два інтеграли по шляху від стану 1 до стану 2 і навпаки – від стану 2 до стану 1, маємо:

;

.

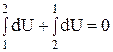Останній вираз вказує на те, що зміна внутрішньої енергії при переході її з одного стану в інший не залежить від шляху процесу, а залежить тільки від початкового і кінцевого стану системи.

За будь-яку температуру (і при 0 К) внутрішня енергія системи більше нуля. При підвищенні температури внутрішня енергія системи зростає, а при фазових перетвореннях (наприклад, плавлення або кипіння) – зростає стрибкоподібно. При сталій температурі внутрішня енергія системи постійна.

Зміна внутрішньої енергії системи відбувається в результаті енергообміну між системою і навколишнім середовищем. Існує дві основні форми енергообміну – теплота і робота.

У разі, коли енергія передається шляхом хаотичного руху частинок тіла, говорять про передачу теплоти. Мірою енергії, що передається шляхом неупорядкованого руху часток системи, є кількість теплоти (Q). У термодинаміці величина Q вважається додатною, якщо теплота поглинається системою, і від'ємною, якщо теплота виділяється системою (правило знаків).

У випадках, коли енергія передається шляхом упорядкованого руху частинок системи, вважають, що відбувається робота. Мірою цієї форми передачі енергії є кількість роботи (W). У загальному випадку робота може бути представлена у вигляді суми декількох різних елементарних робіт – роботи розширення чи стиснення (об'ємна робота), хімічної роботи, роботи руху електричного заряду в електричному полі, роботи проти гравітаційних чи магнітних сил тощо. У кожному конкретному випадку слід визначати, які види робіт мають місце в досліджуваній системі і використовувати їх в рівнянні (1.1). Для багатьох металургійних систем і процесів має практичне значення лише об'ємна робота (W_об), яка може бути визначена за рівнянням

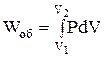. (1.2)

Сума інших видів робіт називається корисною роботою і позначається W'. Тоді маємо W = W_об + W'. Корисна робота для основних металургійних процесів, не пов'язаних з електрохімічними джерелами енергії, звичайно приймається рівною нулю (W' = 0). У термодинаміці роботу вважають додатною, якщо система виконує роботу, і від'ємною, якщо робота виконується над системою.

В рівнянні (1.1) тільки внутрішня енергія є функцією стану системи і її диференціал має властивості повного диференціалу. На відміну від внутрішньої енергії, поняття теплоти і роботи відносяться не до системи, а до процесів. Теплота і робота не є функціями стану системи, вони залежать від шляху процесу і їх диференціали не є повними диференціалами. Тому перший закон термодинаміки в диференціальній формі для нескінченно малих процесів має вигляд

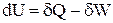, (1.3)

де dQ і dW –нескінченно малі зміни теплоти і роботи при процесі.

1.3. Застосування першого закону термодинаміки до важливіших

термодинамічних процесів

При застосуванні першого закону термодинаміки до найбільш поширених процесів користуються деякими законами ідеальних газів. До реальних газів ці закони можуть застосовуватись лише за певних умов. Головними причинами, що викликають відхилення властивостей реальних газів від властивостей ідеального газу, є наявність у них власного об'єму і взаємного притягання між молекулами, що не враховується при виведенні законів ідеального газу. Взаємне притягання (взаємодія) молекул посилюється із зменшенням відстані між ними. При цьому зростає також частка простору, яку займають самі молекули газу. Таким чином, при зменшенні об'єму, який займає газ (внаслідок підвищення тиску або зниження температури), будь-який реальний газ буде давати все більші відхилення від властивостей ідеального газу. І навпаки, при достатньому зниженні тиску або підвищенні температури реальний газ знаходиться у стані, коли закони ідеальних газів можна застосовувати до нього з будь-яким ступенем точності. Більшість металургійних процесів відбуваються при низькому і сталому тиску та високих температурах. Тому до них можна застосовувати закони ідеальних газів.

Розглянемо ізохорний процес (V = const). Згідно з першим законом термодинаміки (1.1):

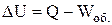при W' = 0;

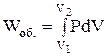; dV = 0; W_об. = 0.

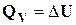. (1.4)

Тобто при сталому об'ємі поглинена системою теплота витрачається на збільшення внутрішньої енергії системи.

При ізобарному процесі (Р = const):

;

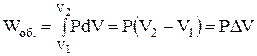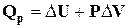. (1.5)

Тобто при сталому тиску поглинена системою теплота витрачається на збільшення внутрішньої енергії системи і виконання об'ємної роботи.

Опрацюємо рівняння (1.5) таким чином:

;

;

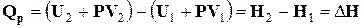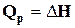. (1.6)

Оскільки U – функція стану системи, а Р і V – параметри стану, то сума U + PV є також функцією стану системи. Ця функція називається ентальпією і позначається символом Н. Визначенням величини Н служить тотожність

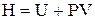. (1.7)

Рівняння (1.6) свідчить про те, що при сталому тиску поглинена системою теплота витрачається на збільшення ентальпії системи.

Ентальпія системи - це повний запас енергії нерухомої системи, на яку діють зовнішні сили (тиск). Оскільки Н – функція стану системи, то її зміна (DН) не залежить від шляху процесу, а залежить лише від початкового і кінцевого стану системи. Вимірюється ентальпія у джоулях (Дж). За будь-яку температуру ентальпія системи додатна (Н > 0). Із зростанням температури ентальпія збільшується, а при фазових перетвореннях – збільшується стрибкоподібно. При сталій температурі ентальпія постійна.

При сталому тиску зміна ентальпії визначається рівнянням

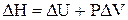, (1.8)

а співвідношення між теплотами ізобарного і ізохорного процесів – рівнянням

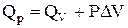. (1.9)

У багатьох випадках зміна ентальпії може бути легко виміряна експериментально, що робить цю функцію дуже важливою в термодинамічних дослідженнях металургійних процесів, оскільки більшість з них протікають при сталому тиску. Абсолютне значення ентальпії не може бути розраховане за допомогою рівнянь термодинаміки, бо воно включає абсолютне значення внутрішньої енергії, яке виміряти не можна.

Для ізотермічного процесу (Т = const), використавши рівняння Менделєєва-Клапейрона

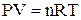, (1.10)

одержуємо

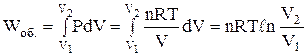
і, враховуючи, що при сталій температурі DU = 0, маємо

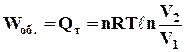, (1.11)

де n – число моль речовини; Т – температура, К; V₁ і V₂ – початковий і кінцевий об'єми системи, м³; R – універсальна газова стала, Дж/(моль×К).

Стала R дійсно є універсальною газовою сталою, оскільки вона не залежить від жодних факторів. Чисельне значення її легко визначається за допомогою рівняння (1.10). Якщо виражати величини рівняння в системі СІ, то значення універсальної газової сталої дорівнюватиме 8,314 Дж/(моль×К).

Фізичний зміст газової сталої можна визначити, якщо рівняння (1.10) написати одного разу для температури Т, а іншого разу для Т + 1, обидва рази для одного моль речовини і однакового тиску. Віднімаючи перше рівняння від другого і позначаючи зміну об'єму через DV, одержуємо R = PDV. Тобто універсальна газова стала дорівнює роботі розширення 1 моль газу при підвищенні температури на 1 К при сталому тиску.

Число моль речовини (n) можна визначити за рівнянням

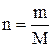, (1.12)

де m – маса речовини, кг; М – молярна (мольна) маса речовини, кг/моль.

При ізобарно-ізотермічному процесі (Р, Т = const), виразивши V₁ і V₂ з рівняння Менделєєва-Клапейрона (1.10):

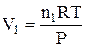і ,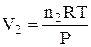

одержимо

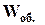
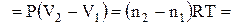
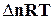, (1.13)

де Dn – зміна числа моль газоподібних речовин при протіканні процесу (реакції).

Наприклад, для реакцій:

С_(Т) + О₂ = СО₂ Dn = 1 моль СО₂ – 1 моль О₂ = 0;

СаСО_3(Т) = СаО_(Т) + СО₂ Dn = 1.

Перехід речовини з одного агрегатного стану в інший при сталих тиску і температурі супроводиться виконанням роботи, яку можна визначити за рівнянням

,

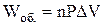де n – число моль речовини; DV – зміна мольного об'єму речовини при переході з одного стану в інший, м³; Р – тиск, Па.

Якщо рідина перетворюється в пару при сталих температурі і тиску, причому тиск дорівнює тиску її насиченої пари, то роботу можна визначити рівнянням

,

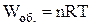де n – число моль речовини; R – універсальна газова стала, Дж/(моль×К); Т – температура випаровування рідини, К.

Задача 1.1. Визначити W_об і DН при плавленні 5,585 кг заліза при тиску 1,013×10⁵ Па і температурі плавлення 1812 К, якщо зміна об'єму системи при плавленні становить 5×10^-7 м³/моль. Теплота плавлення заліза (Q_пл) за цих умов дорівнює 15,49 кДж/моль.

Розв'язання. Плавлення заліза при сталому тиску супроводиться збільшенням ентальпії, яке можна визначити за рівнянням (1.6)

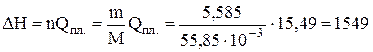кДж.

Робота, виконана системою при плавленні 5,585 кг заліза, дорівнюватиме

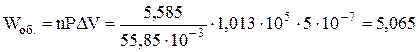Дж.

Задача 1.2. 20 кг доменного газу, взятого при тиску 1,013×10⁵ Па, стискають ізотермічно (Т = 350 К) до об'єму 6,00 м³. Мольна маса газу складає 52×10^-3 кг/моль. Визначити теплоту, роботу і кінцевий об'єм газу.

Розв'язання. При ізотермічному процесі DU = 0, а

.

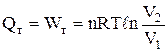Початковий об'єм газу знайдемо з рівняння Менделєєва-Клапейрона

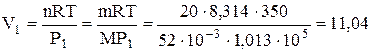м³,

а кінцевий тиск – з рівняння закону Бойля-Маріотта

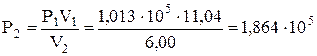Па.

Тоді

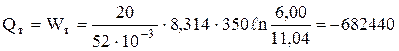Дж = -682,44 кДж.

Date: 2015-05-08; view: 587; Нарушение авторских прав