Адсорбция изотермасы

Көптеген зерттеулер көрсетіп отырғандай, газ қысымы (концентрациясы) артқанда адсорбция мәні артады екен. Бұл шексіз емес. Тұрақты температурада адсорбцияланатын әрбір газ үшін белгілі бір мерзімнен кейін адсорбент бетінде адсорбцияның шекті шамасы орнайды да, екі фаза арасында тепе-теңдік қалыптасады. Адсорбцияның қысымға тәуелділігін өрнектейтін, қисықты адсорбция изотермалары деп атайды. Олар адсорбциялық процестердегі маңызды сипаттамалардың бірі

Мұндайда адсорбция толық қанығады және қысымның артуы адсорбцияға ешбір әсер етпейді. Осылайша адсорбция мен газ қысымының (концентрациясының) арасындағы тура пропорционалдықты көрсететін тәуелділік жоғалады. Бұлжағдай тәжірибе кезінде алынған деректерді тура өрнектейтін математикалық теңдеуді керек етеді. Осы күнге дейін пайдаланып келе жатқан мұндай теңдеуді бірінші болып Фрейндлих ұсынды:

x/m = Kp^1/n (21)

мұндағы x/m – бірлік өлшеміндегі адсорбцияның адсорбент массасындағы шамасы, p – адсорбент үстіндегі газдың тепе-теңдіктегі қысымы (оны ерітінділер үшін тепе-теңдіктегі концентрациямен С алмастырады), K және 1/n – адсорбция константалары, олар белгілі шектерде жүретін адсорбция процесін сипаттайды және өзі соған тән, олардың мәнін тәжірибе кезіндегі алынған мәліметтерге сүйеніп табады.

Фрейндлих теңдеуіне енетін константалардың мәнін түсіну үшін, оны 4-суретте көрсетілген график бойынша талдайды. 4, а-суретте кәдімгі адсорбцияның концентрацияға байланысы кескінделген. Суретте концентрация өскен сайын адсорбцияның оған пропорционалды өсетінін көреміз, бұл изотерманың бастапқы (1) бөлігі, сонан соң концентрация мен адсорбция мәні сәйкес өзгермейді (2). Концентрацияның онан әрі артуы адсорбцияға ешбір ықпал етпейді, ол абцисса осіне параллель күйі қалады (3). Демек, жалпы адсорбция изотермасын үшке бөлуге болады және оның біріншісіне тура пропорционалдық сақталады, бұл кезде адсорбция жылдамдығы үнемі өседі, сонан соң екінші бөлімде шамалы ғана өсіп, үшінші бөлімде адсорбция өзінің шегіне жетеді де адсорбциялық процесте тепе-теңдік орнайды. Осы орайдағы адсорбцияны тепе-теңдік адсорбциясы, ал оған сәйкес концентрацияны шекті не тепе-теңдік концентрациясы дейді.

Фрейндлих теңдеуін логарифмдейік:

lg x/m = lg K + ¹/nlg C (22)

Енді осы түзу сызықты өрнектейтін теңдеуді (11) пайдаланып, б-суретте көрсетілгендей К және ¹/n константалардың мәнін табады.

Көптеген зертттеулер мен тәжірибелер көрсетіп отырғандай, Фрейндлих теңдеуін пайдаланып есептелген адсорбцияның теориялық мәні мен концентрациясының (қысымның) өте аз және аса жоғары кездегі есептелген практикалық мәні сәйкес келе бермейді, яғни теңдеудегі К және ¹/n константаларының физикалық мәні болмайды. 1917 жылы Ленгмюр шыны, слюда, монокристалл сияқты аса жылтыр, тегіс беттерге газдардың адсорбциялануына арналған адсорбцияның өте қарапайым теңдеуін қорытындылап шығарады. Кейінірек бұл теңдеуді басқа да беттерге қолдана беруге болатыны дәлелденді. Ленгмюр өз теңдеуін қорытындылар кезде адсорбциялық қабатты бір молекулалық қабаттан (мономолекулалық) тұрады деп есептеді, яғни адсорбциялайтын заттың (адсорбенттің) беткі қабатымен адсорбцияланатын заттың тек бір молекуладан ғана тұратын қабаты молекулалық ілінісу күшімен байланысты. Сондай-ақ осы тұстағы қойылған шартқа орай, адсорбцияланған бір молекулалық және қабат осындағы адсорбциялық күшті өзіне толық дарытып (сіңіріп) алғандықтан, екінші адсорбциялық қабат түзілмейді.

Ғалым активті орталықтың санын 1-ге тең деп, осы активті орталықтың молекулалармен байланыса адсорбцияланған бөлігін х деп алды. Сонда осы беттің байланыспай қалған бөлігі (1-х) болады. Адсорбцияның шамасын Г арқылы белгілейді. Егер алынған жүйеде ешбір адсорбция жүрмесе, онда х = 0 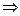Г =0. Ал егер адсорбция құбылысы өте жақсы жүрсе және ондағы барлық активті орталар адсорбцияланатын молекулалармен толық толтырылса, онда х=1, ал Г = Г_∞. Осындай талдаулардан кейін ол х = Г: Г_∞ екенін, яғни адсорбцияланған активті орталықтың шамасы (ауданы) адсорбция мен шексіз адсорбция қатынастарына тең екенін анықтады. Мұндағы Г- толық қаныққан кездегі бірлік өлшемдегі беткі қабаттың адсорбцияланған заттың шамасы.

Тұрақты температура болғанда қатты денедегі адсорбенттік бетте қозғалмалы тепе- теңдік орнайды және осы кездегі адсорбция жылдамдығы (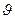 _а) десорбция жылдамдығына ( 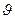_g) теңеледі. Мұнда барлық гетерогенді процестердегідей, адсорбция жылдамдығы бос бетке соғылатын молекула санына, яғни газдың көлемдік концентрациясы (С) мен бос бет үлесіне (1-х) пропорционалды:

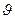_а = К_а С (1-х) (23)

мұндағы К_а – адсорбция жылдамдығының константасы.

Ал десорбция процесінің жылдамдығы тек активті беттерде адсорбцияланған молекулалармен жабылған беттің дәрежесіне ғана тәуелді, газ концентрациясына _gбайланысты емес:

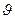_g= _g x (24)

мұндағы K_g – десорбция жылдамдығының константасы.

(24) теңдеуден адсорбциядағы беттің жабылу дәрежесі артқан сайын, адсорбент бетінен бөлініп кеткен молекула саны да артатыны аңғарылады. Адсорбция жылдамдығының константасы мен десорбция жылдамдығының константалары әр түрлі өлшемде: К_а = C^{- 1} K_g = кмоль∙м^-3∙с^-1. Адсорбциялық тепе – теңдік орнағанда, адсорбция жылдамдығы десорбция жылдамдығына тең болады: 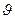_а = 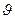_g . Ендеше

К_а С (1-х) = K_gx (25)

Бұл теңдеуден:

x = K_a C / (K_g + K_a C) (26)

Егер осы теңдеудің сол жақ бөлігінің алымын да бөлімін де К_а –ға бөлсе:

x = C / K_g/K_a + C (27)

Мұндағы K_g/K_a = const, оны В әрпімен белгілеп, х-ті Г/Г_∞ -мен алмастырса:

Г/Г_∞ = С/ (С+В) (28)

Г= Г_∞ С / (С+В) (29)

Бұл теңдеуді Ленгмюрдің адсорбция изотермалық теңдеуі дейді. Ол асимптоты Г = Г_∞ болатын гипербола теңдеуін

Енді осы теңдеуді талдап көрелік. Егер концентрация шексіздікке ұмтылса, онда Г = Г_∞. Егер концентрация мәні В-дан әлдеқайда артық болса (С>>В), онда В шамасын ескермеуге болады және Г = Г_∞. Ал (С<<В) болса, онда Г=Г_∞ С/С+В; Г=1 / В Г_∞ С. В коэффициентінің мәні координата басынан гиперболаға жүргізілген жанама түзу осы гиперболаның асимптотын кесіп өткен кесіндімен анықталады (Г=Г_∞), яғни бұл коэффи-

циент гиперболаның көлбеулігін анықтап, заттардың адсорбциялық активтілігі неөлшем болады.

Егер адсорбция жартылай жүрсе (Г =Г/2), онда шексіз адсорбция Г_∞/2 = Г_∞+С/ (С+В) болады және С+В =2С, В=С. Осылайша Ленгмюр теңдеуіндегі В константасы адсорбенттің активті бетінің бір жартысы адсорбтив молекуласымен жабылып (адсорбцияланып), ал екінші жартысы әлі бос күйіндегі концентрация мәнімен өлшенеді.

Көптеген тәжірибе нәтижелері мен есептеулер көрсетіп отырғандай, адсорбция изотермасын сипаттайтын Ленгмюр теңдеуін басқалармен салыстырғанда ол адсорбцияланатын заттың концентрациясы мәніне тәуелсіз адсорбция процесін қанағаттандыратын шамалар береді. Ленгмюр теңдеуін Фрейндлих теңдеуімен салыстырғанда, ондағы теңдеу құрамына енетін тұрақты коэффициенттердің белгілі бір физикалық мәнді түсіндіріп, теориялық пікірге қайшы келмейтіні байқалады.

Ленгмюр теңдеуі адсорбциялық қабат мономолекулалық деген есептен шығады. Алайда бұл пікірмен барлық ғалымдар келісе бермейді. Мысалы, Поляни және басқа да ғалымдардың ойынша, адсорбциялық қабат бір молекуладан тұрмайды, олар екі және одан да көп молекула қабатынан тұрады. Бұл пікірге арналған теория да бар және осы теорияға қайшы келместен, оны дәлелдейтін тәжірибелер де бар.

Ленгмюр теориясы бойынша, жекеленген активті нүктелерге тартылған адсорбтив молекулалары өзара әрекеттеспейді. Бірақ та адсорбциялық қабатта жинақталған, жоғарғы молекулалық массалары бар молекулалар арасында өзара ілінісу күші пайда болуы мүмкін. Мұндай жағдайда Ленгмюр теңдеуі дұрыс шешім бермейді. Кейбір жағдайларда, айталық көмір, силикагель және де басқа қуыс, кеуек адсорбенттерді пайдаланғанда Ленгмюр теңдеуінен гөрі Фрейндлих теңдеуі дұрыс шешім береді.

Date: 2015-05-08; view: 3043; Нарушение авторских прав