Статистика заполнения ПС

Рассмотрим, как меняется заряд ПС при изменении величины поверхностного потенциала ψ _s. Функцию заполнения ПС возьмем в виде функции Ферми – Дирака. Величина энергии Ферми на поверхности полупроводника F _s будет равна:

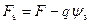. (3.67)

Расстояние от уровня Ферми на поверхности F _s до энергетического уровня ПС E _t, входящее в функцию Ферми – Дирака, равняется:

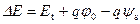, (3.68)

где E _t – энергия ПС, отсчитанная от середины запрещенной зоны. Для ПС в верхней половине запрещенной зоны E _t > 0, в нижней E _t < 0.

Функция заполнения для ПС будет иметь вид:

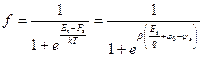. (3.69)

Для моноэнергетических акцепторных ПС заряд Q _ss отрицателен и равен по величине:

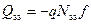, (3.70)

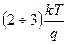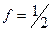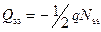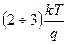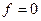где N _ss – плотность моноэнергетических состояний, т.е. их число на единицу площади. Если уровень Ферми на поверхности F _s выше уровня ПС на , то согласно (3.69) f = 1 и Q _ss = - qN _ss. Если уровень Ферми F _s совпадает с уровнем ПС, то и . И наконец, если уровень Ферми ниже уровня ПС на , то и .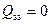

Для моноэнергетических донорных ПС можно с учетом определения, сделанного в разделе 3.1, и свойств функции заполнения записать аналогичное (3.70) выражение.

При квазинепрерывном энергетическом распределении ПС основной величиной, характеризующей ПС, является энергетическая плотность ПС N _ss(E), имеющая размерность [см^-2·эВ^-1].

По смыслу величина N _ss(E) есть плотность состояний на единичный энергетический интервал dE = 1 вблизи значения энергии E, а величина N _ss(E) dE дает число состояний на единицу площади в энергетическом интервале (E; E + dE). Если величина N _ss(E) не зависит от энергии, т.е. плотность ПС постоянна по ширине запрещенной зоны полупроводника, для заряда ПС Q _ss имеем с точностью до размытия функции распределения:

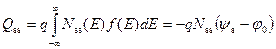. (3.71)

Из соотношения (3.71) следует, как это видно из рисунка 3.9, что при ψ _s < φ ₀ заряд ПС Q _ss положителен, при ψ _s = φ ₀ заряд Q _ss равен нулю и при ψ _s > φ ₀ заряд Q _ss отрицателен.

Поскольку, как следует из соотношений (3.70) и (3.71), заряд ПС не зависит от поверхностного потенциала ψ _s и изменяется при изменении последнего, ПС должны обладать определенной емкостью C _ss, называемой емкостью поверхностных состояний.

Для моноэнергетических ПС:

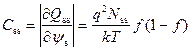. (3.72)

Исследование соотношения (3.72) показывает, что зависимость C _ss(ψ _s) имеет вид колоколообразной кривой с шириной на полувысоте, равной 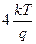и имеющей максимум при пересечении уровнем Ферми на поверхности энергетического уровня ПС, что соответствует условию 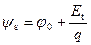. В области максимума величина 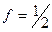, поэтому максимальное значение емкости ПС

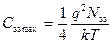. (3.73)

При квазинепрерывном спектре ПС величина емкости C _ss ПС, согласно (3.71), равна

. (3.74)

При экспериментальных измерениях емкость ПС C _ss подключается параллельно емкости ОПЗ C _sc. Минимального значения емкость ОПЗ C _sc достигает в области слабой инверсии при ψ _s ≈ 2 φ ₀. Для кремния при концентрации акцепторов N _A = 1,5·10¹⁵ см^-3 и комнатной температуре, как следует из соотношения (3.57), величина емкости ОПЗ C _sc = 1,6·10^-8 Ф/см². Энергетическая плотность ПС N _ss, обеспечивающих емкость ПС C _ss, равную емкости ОПЗ C _sc, будет, согласно (3.74), N _ss = 10¹¹ см^-2эВ^-1. Таким образом, если плотность ПС на границе раздела полупроводника со средой существенно меньше приведенной цифры, то следует ожидать, что в емкостных измерениях ПС не проявляются.

3.6. Вольт‑фарадные характеристики структур МДП

3.6.1. Устройство МДП‑структур и их энергетическая диаграмма

Структуры металл – диэлектрик – полупроводник, или сокращенно МДП‑структуры, широким интересом к изучению их физических свойств обязаны появлению планарной технологии и развитию нового класса полупроводниковых приборов, работающих на основе эффекта поля, таких как приборы с зарядовой связью, полевые транзисторы с изолированным затвором, репрограммируемые элементы памяти с плавающим затвором и т.п. МДП‑структуры позволяют анализировать основные процессы, протекающие в такого рода приборах, и являются чрезвычайно удобными объектами исследования. Устройство МДП‑структуры следует из ее названия.

МДП-структура представляет собой монокристаллическую пластину полупроводника, называемую подложкой, закрытую с планарной стороны диэлектриком. Металлический электрод, нанесенный на диэлектрик, носит название затвора, а сам диэлектрик называется подзатворным. На обратную непланарную сторону полупроводниковой пластины наносится металлический электрод, называющийся омическим контактом. Довольно часто в качестве диэлектрика в МДП-структурах используют окислы, поэтому вместо МДП употребляется название МОП‑структура [14, 11, 13]. Итак, МДП‑структура, приведенная на рисунке 3.10, состоит из затвора, подзатворного диэлектрика, полупроводниковой подложки и омического контакта.

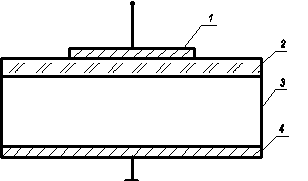
Рис. 3.10. Устройство МДП‑структуры

1 – затвор, 2 – подзатворный диэлектрик, 3 – полупроводниковая подложка, 4 – омический контакт

Рассмотрим зонную энергетическую диаграмму МДП‑структуры при равновесных условиях. Согласно правилу построения зонных диаграмм необходимо, чтобы в системе при отсутствии приложенного напряжения:

а) уровень вакуума был непрерывен;

б) электронное сродство диэлектрика и полупроводника в каждой точке было постоянно;

в) уровень Ферми был одинаков.

На рисунке 3.11а приведена построенная таким образом зонная диаграмма для идеальной МДП‑структуры. Под идеальной МДП‑структурой будем понимать такую систему металл – диэлектрик – полупроводник, когда:

- отсутствуют поверхностные состояния на границе раздела полупроводник – диэлектрик,

- термодинамические работы выхода металла затвора и полупроводника подложки равны между собой,

- отсутствуют заряженные центры в объеме подзатворного диэлектрика,

- сопротивление подзатворного диэлектрика бесконечно велико, так что сквозной ток через него отсутствует при любых напряжениях на затворе.

На рисунке 3.11б, в приведены зонные диаграммы идеальных МДП‑структур при различных полярностях приложенного напряжения V _G к затвору.

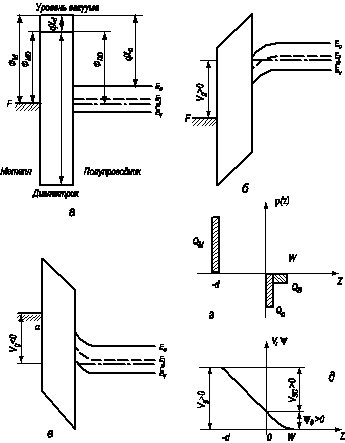
Рис. 3.11. Зонная диаграмма идеальной МДП‑структуры с полупроводником p ‑типа:

а) V _G = 0; б) V _G > 0; в) V _G < 0; г) распределение зарядов в МДП‑структуре при V _G > 0; д) распределение приложенного напряжения V _G между диэлектриком и полупроводником

МДП‑структуры, близкие к идеальным, получают, используя «хлорную» технологию термического выращивания двуокиси кремния на кремнии, причем для n ‑Si в качестве материала затвора используется алюминий, а для p ‑Si используется золото.

МДП‑структуры, в которых нарушается одно из вышеперечисленных требований, получили название реальных МДП‑структур, рассмотрение свойств которых далее и проводится.

Date: 2015-05-05; view: 587; Нарушение авторских прав