Уравнение электронейтральности

Рассмотрим более подробно связь между напряжением на затворе V _G МДП‑структуры и поверхностным потенциалом ψ _s. Все приложенное напряжение V _G к МДП‑структуре делится между диэлектриком и полупроводником, причем очевидно, что падение напряжения в полупроводнике равняется поверхностному потенциалу ψ _s.

Таким образом,

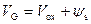. (3.75)

Из (3.75) и анализа зонных энергетических диаграмм на рисунке 3.11 следует, что знак поверхностного потенциала ψ _s, выбранный нами ранее a priori, в действительности соответствует знаку напряжения на затворе V _G. Действительно, положительное напряжение на затворе идеальной МДП-структуры вызывает изгиб зон вниз у полупроводников n‑ и p ‑типа, что соответствует положительным значениям поверхностного потенциала. Отрицательное напряжение V _G вызывает изгиб зон вверх у поверхности полупроводника, что соответствует отрицательному значению поверхностного потенциала ψ _s.

Из условия электронейтральности следует, что заряд на металлическом электроде Q _M должен быть равен суммарному заряду в ОПЗ Q _sc, заряду поверхностных состояний на границе раздела полупроводник-диэлектрик Q _ss и встроенному заряду в диэлектрик вблизи границы раздела Q _ox.

Тогда

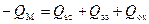. (3.76)

Согласно определению геометрической емкости диэлектрика C _ox,

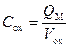, (3.77)

отсюда

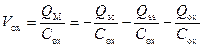. (3.78)

Учитывая, что между металлом и полупроводником существует разность термодинамических работ выхода Δ φ _ms, получаем:

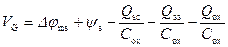. (3.79)

Из соотношения (3.79) следует, что если V _G > 0, то ψ _s > 0, величины Q _sc < 0, Q _ss < 0, т.е. падение напряжения на диэлектрик V _ox > 0. Аналогично будет соотношение знаков и при V _G < 0. Поскольку нами было показано ранее, что

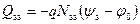, (3.80)

подставив (3.80) в (3.79), имеем:

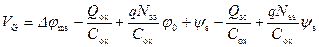. (3.81)

Введем новое обозначение – напряжение плоских зон V _FB (Flat Band). Напряжением плоских зон V _FB называется напряжение на затворе реальной МДП-структуры, соответствующее значению поверхностного потенциала в полупроводнике, равному нулю:

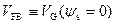. (3.82)

С учетом определения (3.82) из (3.81) следует:

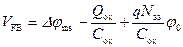. (3.83)

Таким образом, связь между напряжением на затворе V _G и поверхностным потенциалом ψ _s с учетом (3.83) задается в виде:

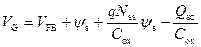. (3.84)

Проведем более подробный анализ (3.84) для различных областей изменения поверхностного потенциала.

Обогащение (ψ _s < 0)

Выражение для заряда в ОПЗ Q _sc описывается соотношением (3.19). Подставляя (3.19) в (3.75), получаем:

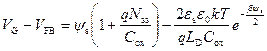. (3.85)

Для больших значений ψ _s (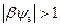), когда Q _sc >> Q _ss, из соотношения (3.85) следует:

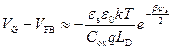. (3.86)

Отсюда

,

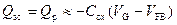. (3.87)

Из (3.86) и (3.87) следует, что при обогащении поверхности дырками, как основными носителями, поверхностный потенциал ψ _s зависит от напряжения на затворе V _G логарифмически, а заряд Q _sc в ОПЗ зависит от напряжения на затворе V _G линейно.

Обеднение и слабая инверсия (0 < ψ _s < 2 φ ₀)

Заряд в ОПЗ Q _sc в этом случае в основном обусловлен ионизованными акцепторами Q _B и выражается соотношением (3.20).

Разложим выражение для Q _B в ряд вблизи ψ _s = φ ₀:

,

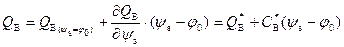здесь Q _B^*, C _B^* – величина заряда и емкости ионизованных акцепторов в ОПЗ при ψ _s = φ ₀.

Подставив выражение для Q _B в (3.84) и учтя выражение для C _B^* (3.57), получаем:

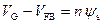, (3.88)

где

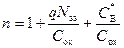. (3.89)

Из соотношения (3.88) следует, что в области обеднения и слабой инверсии поверхностный потенциал ψ _s зависит от напряжения V _G линейно, причем тангенс угла наклона 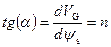определяется плотностью поверхностных состояний N _ss, толщиной подзатворного диэлектрика d _ox и уровнем легирования полупроводниковой подложки N _A.

Сильная инверсия (ψ _s > 2 φ ₀)

Заряд в ОПЗ Q _sc отрицателен, состоит из заряда ионизованных акцепторов Q _B и электронов Q _n в инверсионном слое. Учитывая выражение (3.22) для Q _n, имеем:

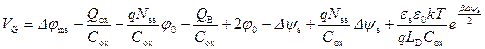, (3.90)

где величина Δ ψ _s = ψ _s - 2 φ ₀.

Введем пороговое напряжение V _T как напряжение на затворе V _G, когда в равновесных условиях поверхностный потенциал ψ _s равен пороговому значению 2 φ ₀.

. (3.91)

Из (3.90) и (3.91) следует, что

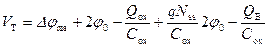, (3.92)

или с учетом определения V _FB

. (3.93)

Из (3.93) следует, что если отсчитывать пороговое напряжение V _T от напряжения плоских зон V _FB, то оно будет состоять из падения напряжения в полупроводнике 2 φ ₀ и падения напряжения на подзатворном диэлектрике за счет заряда ионизованных акцепторов и заряда в поверхностных состояниях. Для достаточно высоких значений ψ _s, когда β Δ ψ _s > 1, имеем:

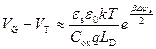. (3.94)

Отсюда

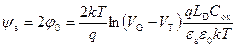, (3.95)

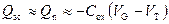. (3.96)

Из (3.95) и (3.96) следует, что в области сильной инверсии, так же как и в области обогащения, поверхностный потенциал логарифмически зависит от напряжения на затворе V _G, а заряд электронов в инверсионном слое Q _n линейно зависит от величины V _G.

На рисунке 3.12 приведена зависимость поверхностного потенциала ψ _s от напряжения на затворе V _G, рассчитанная для различных толщин подзатворного диэлектрика d _ox.

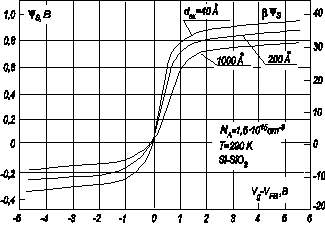
Рис. 3.12. Зависимость поверхностного потенциала ψ _s от напряжения на затворе V _G, рассчитанная из уравнения (3.84) для кремниевой МДП‑структуры с различной толщиной подзатворного диэлектрика

3.6.3. Емкость МДП‑структур

Одним из наиболее распространенных методов изучения свойств структур металл – диэлектрик – полупроводник является метод, основанный на анализе зависимости емкости МДП‑структуры C _МДП от напряжения на затворе V _G, так называемый метод вольт‑фарадных характеристик (ВФХ) или C ‑ V метод. Для использования этого метода рассмотрим подробно теорию емкости МДП-структур. В дальнейшем величину удельной емкости МДП‑структуры будем просто обозначать меткой C без индексов. Согласно определению емкости,

. (3.97)

Используя выражения для заряда на затворе Q _M из (3.77) и для падения напряжения на диэлектрике V _ox из (3.75), получаем:

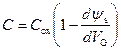. (3.98)

Таким образом, зависимость C МДП‑структуры от напряжения будет определяться полученной нами ранее зависимостью ψ _s(V _G), приведенной на рисунке 3.12. Сразу же можно из анализа (3.86) и (3.98) сказать, что в области сильной инверсии и обогащения емкость C будет слабо зависеть от величины V _G, выходя на насыщение при больших V _G. В области обеднения и слабой инверсии следует ожидать, согласно (4.14), участка с почти постоянной величиной емкости. Общая зависимость емкости от напряжения будет иметь вид кривой с ярко выраженным минимумом.

Воспользуемся выражением (3.84) для напряжения на затворе V _G и продифференцируем (3.79) по ψ _s.

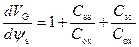, (3.99)

где C _ss, C _sc – емкость поверхностных состояний и емкость ОПЗ, определенные ранее.

Подставляя (3.99) в (3.98) и проводя преобразования, получаем:

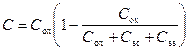(3.100)

или

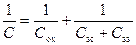. (3.101)

Соотношение (3.101) позволяет нам построить эквивалентную схему МДП‑структуры, представив ее как последовательно соединенную емкость диэлектрика C _ox с параллельной цепочкой емкости ОПЗ C _sc и поверхностных состояний C _ss.

На рисунке 3.13 приведена эквивалентная схема емкости МДП‑структуры. Отметим, что такую схему можно было нарисовать исходя из общих соображений об устройстве МДП‑структур.

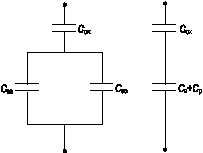
Рис. 3.13. Простейшая эквивалентная схема МДП‑структуры

На рисунке 3.14 приведены равновесные C ‑ V кривые идеальных МДП‑структур с разной толщиной диэлектрика, рассчитанные по уравнению (3.109).

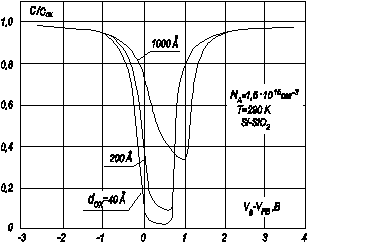
Рис. 3.14. Равновесные C ‑ V характеристики идеальных МДП‑структур на кремнии p ‑типа с различной толщиной подзатворного диэлектрика

3.6.4. Экспериментальные методы измерения вольт‑фарадных характеристик

При экспериментальном измерении вольт‑фарадных характеристик МДП‑структур важное значение имеет частота измерительного сигнала ω. Это связано с тем, что процессы захвата и выброса на поверхностные состояния, а также изменения заряда свободных носителей в инверсионном слое, характеризующие соответствующие емкости C _ss и C _sc, имеют конечные времена τ, сравнимые с периодом обычно используемого в эксперименте сигнала. Напомним, что изменение заряда Q _n в инверсионном слое характеризуется генерационно-рекомбинационным процессом и определяется временем жизни неосновных носителей τ _n в ОПЗ. Характерное время захвата и выброса на поверхностные состояния определяется постоянной времени τ этих состояний. В зависимости от частоты измерительного сигнала различают два метода – метод высокочастотных C ‑ V характеристик и квазистатический C ‑ V метод.

Квазистатический C ‑ V метод

В области низких частот, когда период измерительного сигнала существенно больше времени жизни неосновных носителей τ _n в ОПЗ и постоянной времени поверхностных состояний τ (ω ^-1 >> τ _n, τ), полная емкость МДП‑структуры определяется суммой всех емкостей, входящих в уравнение (3.99). Вольт‑фарадная характеристика, измеренная при этом условии, получила название равновесной низкочастотной C‑V кривой. Характерный вид таких кривых обсуждался ранее (см. рис. 3.14).

Экспериментально низкочастотные кривые получают, обычно используя квазистатический C ‑ V метод. Сущность этого метода сводится к тому, что измеряется ток смещения через МДП‑систему при линейной развертке напряжения V _G, и величина тока смещения I _см оказывается пропорциональной емкости МДП‑структуры. Действительно, если

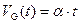, (3.102)

то величина тока смещения I _см, согласно (3.97),

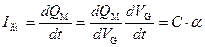. (3.103)

Если емкость МДП-структуры зависит от напряжения C = C (V _G), то и ток смещения также будет зависеть от напряжения I _см = I _см(V _G).

Требование низкой частоты ω ^-1 >> τ _n, τ для измерения равновесных низкочастотных кривых обуславливает малые величины скорости изменения напряжения 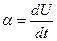в уравнении (3.103). Обычно величина α составляет α = 10^-4÷10^-2 В/с.

При этих условиях ток смещения через МДП‑структуру мал (I _см ≤ 10^-9÷10^-12 А) и для его измерения необходимо пользоваться электрометрическими вольтметрами. На рисунке 3.15 приведена схема реализации квазистатического метода. Для получения абсолютного отсчета емкости используются калибровочные емкости с малыми сквозными утечками, подключаемые вместо МДП‑структур.

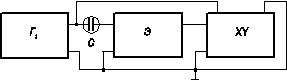
Рис. 3.15. Схема измерения квазистатических вольт‑фарадных характеристик МДП‑структур:

Г ₁ – генератор пилообразного напряжения, Э – электрометрический усилитель, XY – двухкоординатный самописец, C – МДП-структура

Метод высокочастотных C ‑ V характеристик

Сущность метода высокочастотных характеристик заключается в том, что используется для измерения емкости МДП‑структуры малый переменный сигнал с периодом, существенно меньшим, чем время жизни неосновных носителей и время перезарядки поверхностных состояний (ω ^-1 << τ _n, τ).

При этих условиях заряд в инверсионном канале Q _n не успевает следовать за изменением переменного напряжения, и емкость неосновных носителей C _n равна нулю. Следовательно, емкость ОПЗ C _sc в (3.99) будет обусловлена в обогащении основными носителями, а в обеднении и инверсии – только слоем обеднения C _B. Поскольку поверхностные состояния не успевают перезаряжаться с частотой переменного тестирующего сигнала, то их емкость также равна нулю (C _ss = 0). Таким образом, емкость МДП‑структуры на высокой частоте определяется только емкостью диэлектрика C ₀ и емкостью области пространственного заряда C _sc без учета емкости неосновных носителей C _n. Кроме малого по амплитуде измерительного напряжения в этом методе к МДП‑структуре прикладывается постоянное напряжение V _G, изменяющее ее емкость C.

Обычно это напряжение V _G подают от генератора линейно меняющегося напряжения. Полученную вольт‑фарадную характеристику записывают на двухкоординатный самописец. На рисунке 3.16 приведена схема этого метода, иногда называемая схемой Гоетцбергера. Выберем соотношение емкости C МДП‑структуры и нагрузочного сопротивления R _H такое, чтобы всегда выполнялось условие 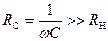. Пусть с генератора переменного напряжения на МДП‑структуру подается малое напряжение 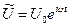, причем 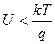. Тогда ток через нашу емкость C и нагрузку R _Н будет:

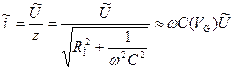. (3.104)

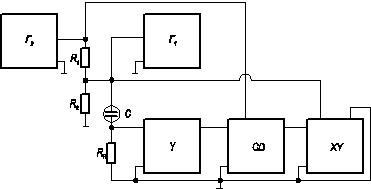
Рис. 3.16. Схема измерения высокочастотных вольт‑фарадных характеристик МДП‑структур

Падение напряжения на нагрузочном сопротивлении 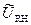равно:

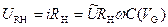. (3.105)

Таким образом, падение напряжения на нагрузочном сопротивлении U _RH пропорционально емкости МДП‑структуры. После усиления этого сигнала узкополосным усилителем и детектирования с использованием синхродетектора для выделения только емкостной составляющей в сигнале, мы получаем отклонение пера на самописце по координате Y, пропорциональное емкости МДП‑системы. Меняя величину V _G и подавая сигнал генератора развертки V _G одновременно на МДП‑структуру и ось X самописца, получаем запись высокочастотной вольт-фарадной характеристики. Для получения абсолютных значений в отсчете емкости вместо МДП‑структуры подключают калибровочную емкость.

3.6.5. Определение параметров МДП‑структур на основе анализа C‑V характеристик

Анализ вольт‑фарадных характеристик позволяет получить обширную информацию об основных параметрах МДП‑структур: типе проводимости полупроводниковой подложки (n‑ или p‑ тип); концентрации легирующей примеси в подложке и законе ее распределения в приповерхностной области полупроводника; величине и знаке встроенного в диэлектрик МДП‑структуры заряда; толщине подзатворного окисла; плотности поверхностных состояний на границе раздела полупроводник – диэлектрик. Рассмотрим более подробно эти вопросы.

Date: 2015-05-05; view: 891; Нарушение авторских прав