Избыток свободных носителей заряда

Важной характеристикой ОПЗ является значение заряда свободных носителей (электронов или дырок) Q _p,n или, если выразить этот заряд в единицах элементарного заряда, величина избытка электронов или дырок G _p,n в ОПЗ. Определим величину G _p как

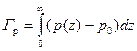, (3.24)

где p (z) – концентрация дырок в ОПЗ, p ₀ – концентрация дырок в квазинейтральном объеме.

Таким образом, избыток электронов или дырок – это избыточное по сравнению с равновесным в нейтральном объеме число свободных носителей на единицу площади ОПЗ. В ряде источников иногда избыток свободных носителей G _p,n называют поверхностной концентрацией. Это не совсем верно, ибо поверхностная концентрация по своему смыслу есть число свободных носителей заряда на единицу объема, рассчитанное на поверхности полупроводника. А избыток G _p,n есть избыточное число свободных носителей, проинтегрированное по глубине ОПЗ и рассчитанное на единицу площади.

Из (3.24) следует, что

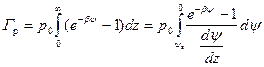. (3.25)

Аналогично избыток электронов G _n равен:

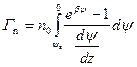. (3.26)

Понятиями избытка G _p,n чаще пользуются, когда говорят о свободных носителях в инверсионном канале. Для случая обогащения выражения (3.25, 3.26), рассчитанные с учетом (3.15), при значениях 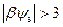будут иметь вид:

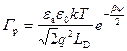, (3.27)

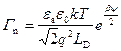. (3.28)

Для области слабой и сильной инверсии выражение для G _p,n можно получить в аналитическом виде из выражений для зарядов в ОПЗ, не прибегая к интегрированию (3.25, 3.26).

Действительно, заряд свободных носителей, например, электронов, в инверсионном канале Q _n равен разности полного заряда Q _sc и заряда ионизованных доноров Q _B, для которых имеются аналитические выражения:

. (3.29)

Для случая инверсии соотношение (3.18) для Q _sc упростится и будет иметь вид:

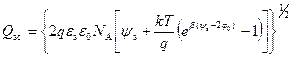. (3.30)

Используя выражения для Q _B в виде (3.20) и (3.23), получаем соответственно для области слабой и сильной инверсии выражения для Q _n в виде:

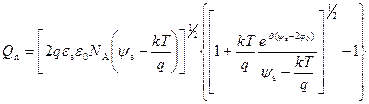, (3.31)

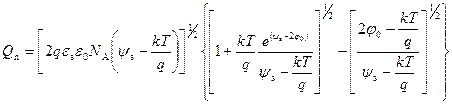. (3.32)

Для случая (3.32), используя соотношение

,

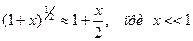получаем:

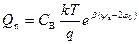. (3.33)

Здесь 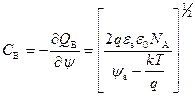– емкость обедненной области.

Для случая (3.33) удовлетворительная аппроксимация существует только при 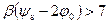и имеет вид:

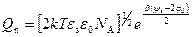. (3.34)

Отметим, что выражение (3.33) совпадает с соответствующим выражением для Q _n в уравнении (3.22). Величина избытка электронов 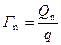будет для области слабой и сильной инверсии при соответствующих ограничениях равна:

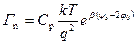, (3.35)

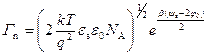. (3.36)

Из соотношения (3.36) при значении y _s = 2 j ₀, т.е. для начала области сильной инверсии, можно получить, что для кремния с удельным сопротивлением r = (1¸10) Ом×см величина избытка G _n(y _s = 2 j ₀) = (10⁹¸10¹⁰) см^-2. Максимальное значение избытка G _n, достигаемое в ОПЗ, составляет G _{n max} = (1¸2)×10¹³ см^-2 и ограничивается пробоем ОПЗ полупроводника.

Из соотношений (1.42 – 1.47) следует, что избыток свободных носителей экспоненциально зависит от значения поверхностного потенциала y _s и слабо зависит от температуры и легирования полупроводника. На рисунках 3.4 и 3.5 приведены соответствующие графики зависимости Q _n и G _n от значения y _s.

Рис. 3.4. Зависимость заряда свободных электронов Q _n в инверсионном канале от поверхностного потенциала y _s, рассчитанная для кремния p ‑типа с различной концентрацией акцепторов

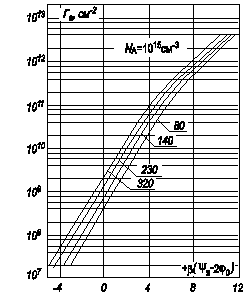
Рис. 3.5. Зависимость избытка электронов G _n в инверсионном канале от поверхностного потенциала y _s, рассчитанная для кремния p ‑типа при различной температуре

Date: 2015-05-05; view: 587; Нарушение авторских прав