Распределение электрического поля и потенциала в барьере Шоттки

Рассмотрим более детально, как меняются электрическое поле и потенциал в области пространственного заряда контакта металл – полупроводник в виде барьера Шоттки. Для определенности будем рассматривать полупроводник n ‑типа. За знак приложенного напряжения примем знак напряжения, приложенного к металлическому электроду, полупроводниковый электрод считаем заземленным.

Вне зависимости от полярности напряжения для барьерных структур все внешнее напряжение будет приложено к области пространственного заряда, поскольку в этой области концентрация свободных носителей существенно меньше, чем в других областях барьера Шоттки.

Связь электрического поля и потенциала для любых материалов с пространственно распределенным объемным зарядом описывается уравнением Пуассона. В одномерном приближении это уравнение имеет вид:

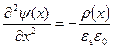, (2.30)

где y (x) – зависимость потенциала от координаты, r (x) – плотность объемного заряда, e _s – диэлектрическая проницаемость полупроводника, e ₀ – диэлектрическая постоянная.

Заряд в области пространственного заряда барьера Шоттки для полупроводника n ‑типа обусловлен зарядом ионизованных доноров с плотностью N _D⁺. Поэтому

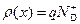. (2.31)

При интегрировании уравнения Пуассона учтем, что величина электрического поля :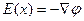

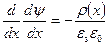, (2.32)

или

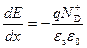. (2.33)

Проведем интегрирование уравнения (2.33). Выберем константу интегрирования из расчета, что при x = W электрическое поле Е равно нулю,

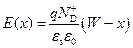. (2.34)

Из соотношения (2.34) следует, что электрическое поле Е максимально на границе металл – полупроводник (x = 0), линейно спадает по области пространственного заряда и равно нулю на границе ОПЗ – квазинейтральный объем полупроводника (x = W).

Для нахождения распределения потенциала (а следовательно, и зависимости потенциальной энергии от координаты) проинтегрируем еще раз уравнение (2.34) при следующих граничных условиях: x = W, y (W) = 0. Получаем (рис. 2.6):

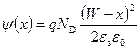. (2.35)

Максимальное значение потенциала реализуется при x = 0 и составляет:

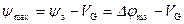, при 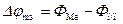. (2.36)

В этом случае можно рассчитать значение ширины обедненной области W, подставляя соотношение (2.36) в (2.35):

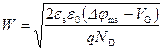. (2.37)

Соотношение (2.37) является очень важным для барьерных структур. В дальнейшем будет показано, что это уравнение является универсальным и описывает зависимость ширины обедненной области W от приложенного напряжения V _G и легирующей концентрации N _D для большинства барьерных структур. На рисунке 2.6 приведена диаграмма, иллюстрирующая распределение электрического поля и потенциала в барьере Шоттки при обратном смещении, рассчитанных на основании соотношений (2.34) и (2.35).

Рис. 2.6. Диаграмма, иллюстрирующая распределение электрического поля и потенциала в барьере Шоттки:

а) структура барьера Шоттки при обратном смещении; б) распределение электрического поля в ОПЗ; в) распределение потенциала в ОПЗ

2.9. Вольт‑амперная характеристика барьера Шоттки

Для рассмотрения вольт‑амперной характеристики (ВАХ) барьера Шоттки воспользуемся диодным приближением.

Вместо критерия 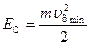для барьера Шоттки воспользуемся для перехода электронов из полупроводника в металл выражением:

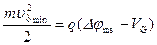. (2.38)

Подставляя это выражение в (2.5) и (2.7), получаем:

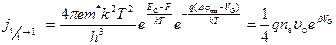, (2.39)

где υ ₀ – тепловая скорость электронов, равная ,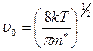

n _s – поверхностная концентрация в полупроводнике на границе с металлом ,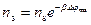

n ₀ – равновесная концентрация основных носителей в полупроводнике, равная 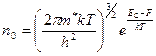[6, 17].

В условиях равновесия V _G = 0 ток из полупроводника в металл 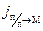уравновешивается током из металла в полупроводник 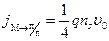. При приложении напряжения этот баланс нарушается и общий ток будет равен сумме этих токов. Следовательно, вольт‑амперная характеристика барьера Шоттки будет иметь вид:

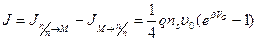; (2.40)

В более компактной форме ВАХ записывается в виде:

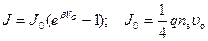. (2.41)

На рисунке 2.7 приведена вольт‑амперная характеристика барьера Шоттки.

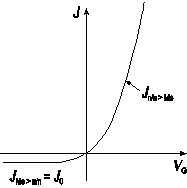
Рис. 2.7. Вольт-амперная характеристика барьера Шоттки

Вольт‑амперная характеристика барьера Шоттки имеет ярко выраженный несимметричный вид. В области прямых смещений ток экспоненциально сильно растёт с ростом приложенного напряжения. В области обратных смещений ток от напряжения не зависит. В обеих случаях, при прямом и обратном смещении, ток в барьере Шоттки обусловлен основными носителями – электронами. По этой причине диоды на основе барьера Шоттки являются быстродействующими приборами, поскольку в них отсутствуют рекомбинационные и диффузионные процессы. Несимметричность вольт-амперной характеристики барьера Шоттки – типичная для барьерных структур. Зависимость тока от напряжения в таких структурах обусловлена изменением числа носителей, принимающих участие в процессах зарядопереноса. Роль внешнего напряжения заключается в изменении числа электронов, переходящих из одной части барьерной структуры в другую.

2.10. Образование и зонная диаграмма р-n перехода

Электронно‑дырочным, или p ‑ n переходом, называют контакт двух полупроводников одного вида с различными типами проводимости (электронным и дырочным).

Классическим примером p ‑ n перехода являются: nSi – pSi, nGe – pGe.

Рассмотрим контакт двух полупроводников n ‑ и p ‑типа. Величина работы выхода Ф определяется расстоянием от уровня Ферми до уровня вакуума. Термодинамическая работа выхода в полупроводнике p ‑типа Ф _p всегда больше, чем термодинамическая работа выхода Ф _n в полупроводнике n ‑типа. Из соотношений (2.13) и (2.14) следует, что

.

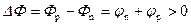При контакте полупроводников n ‑ и p ‑типов вследствие различного значения токов термоэлектронной эмиссии (из-за разных значений работы выхода) поток электронов из полупроводника n ‑типа в полупроводник p ‑типа будет больше. Электроны из полупроводника n ‑типа будут при переходе в полупроводник p -типа рекомбинировать с дырками. Вследствие несбалансированности токов в полупроводнике n ‑типа возникнет избыточный положительный заряд, а в полупроводнике p ‑типа – отрицательный. Положительный заряд обусловлен ионизованными донорами, отрицательный заряд – ионизованными акцепторами. Вследствие эффекта поля произойдет изгиб энергетических зон в полупроводниках n ‑ и p ‑типов, причем в полупроводнике p -типа на поверхности термодинамическая работа выхода будет уменьшаться, а в полупроводнике n ‑типа на поверхности термодинамическая работа выхода будет увеличиваться. Условию термодинамического равновесия соответствуют равные значения токов термоэлектронной эмиссии с поверхности полупроводников p ‑ и n ‑типов, а следовательно, и равные значения термодинамической работы выхода.

На рисунке 2.8 приведены зонные диаграммы, иллюстрирующие этапы формирования электронно‑дырочного перехода.

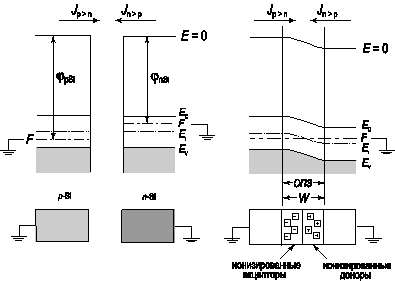
Рис. 2.8. Схема, иллюстрирующая образование p‑n перехода

Граница областей донорной и акцепторной примеси в полупроводнике получила название металлургического p‑n перехода. Границу, где уровень Ферми пересекает середину запрещенной зоны, называют физическим p‑n переходом.

2.10.1. Распределение свободных носителей в p‑n переходе

Рассмотрим несимметричный p‑n переход, будем считать, что концентрация акцепторов больше, чем концентрация доноров N _A > N _D; в этом случае для объемного положения уровня Ферми получаем j _n < j _p. В условиях равновесия (V _G = 0) высота потенциального барьера p‑n перехода будет:

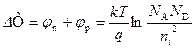. (2.42)

Рассмотрим распределение свободных носителей – электронов и дырок в области пространственного заряда p‑n перехода.

Для квазинейтрального объема полупроводников

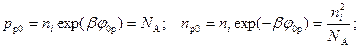
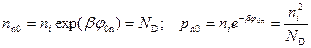. (2.43)

Для области пространственного заряда эти соотношения трансформируются таким образом, что j _0p и j _0n становятся зависимыми от координаты x, то есть j _0p(x) и j _0n(x). Следовательно, и концентрации электронов и дырок в области пространственного заряда тоже будут зависеть от координаты x: p _p(x), n _p(x), n _n(x), p _n(x).

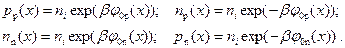(2.44)

Рассмотрим, как меняется концентрация основных и неосновных носителей в ОПЗ полупроводника p -типа. В p‑n переходе величина j _p квазилинейно уменьшается, поэтому концентрация дырок p _p будет экспоненциально убывать. Уровень Ферми совпадает с серединой запрещенной зоны у физического p‑n перехода (j _p = 0), в этой точке концентрация дырок становится равной собственной концентрации, т.е. p _p = n _i.

Для электронов аналогично получаем, что величина концентрации электронов n _p(x) возрастает экспоненциально и также равна собственной концентрации в области физического p‑n перехода.

Аналогично меняется концентрация основных n _n(x) и неосновных p _n(x) носителей в ОПЗ полупроводника n -типа.

На рисунке 2.9 показано распределение концентрации носителей в несимметричном p‑n переходе в логарифмическом масштабе и схема p‑n перехода.

Рис. 2.9. p‑n переход в равновесных условиях:

а) распределение равновесных носителей; б) диаграмма, иллюстрирующая распределение доноров и акцепторов

Таким образом, из приведенного рисунка следует, что в несимметричных p‑n переходах физические и металлургические p‑n переходы пространственно не совпадают. Распределение концентрации основных и неосновных носителей симметрично относительно линии, соответствующей собственной концентрации n _i.

2.10.3. Поле и потенциал в p‑n переходе

Связь электрического поля и потенциала в p‑n переходе описывается уравнением Пуассона. В одномерном приближении это уравнение имеет вид:

, (2.45)

где y (x) – зависимость потенциала от координаты, r (x) – плотность объемного заряда, e _s – диэлектрическая проницаемость полупроводника, e ₀ – диэлектрическая постоянная.

Для рассмотрения этого уравнения выберем начало координат в области металлургического p‑n перехода. При этом донорный полупроводник будет находиться в области x > 0 (в дальнейшем обозначим цифрой I), а акцепторный – в области x < 0 (в дальнейшем обозначим цифрой II).

Заряд в области пространственного заряда p‑n перехода для полупроводника n ‑типа обусловлен зарядом ионизованных доноров с плотностью N _D⁺_, для полупроводника p ‑типа – зарядом ионизованных акцепторов с плотностью N _A⁺. Поэтому для области I 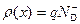, для области II 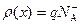. Будем решать уравнение Пуассона отдельно для областей I и II. После интегрирования уравнения Пуассона получаем для области I:

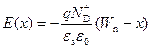, (2.46)

для области II:

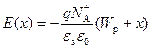. (2.47)

Знак минус в выражениях (2.46, 2.47) указывает, что направление электрического поля противоположно направлению оси x.

Из соотношения (2.34) следует, что электрическое поле Е максимально на металлургической границе p‑n перехода (x = 0), линейно спадает по области пространственного заряда и равно нулю на границах ОПЗ – квазинейтральный объем полупроводника (x = W _n; x = W _p).

Максимальная величина электрического поля E _max будет равна:

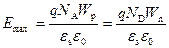. (2.48)

Для нахождения распределения потенциала (а следовательно, и зависимости потенциальной энергии от координаты) проинтегрируем еще раз уравнение (2.34) при следующих граничных условиях: x = W, y (W) = 0. Получаем:

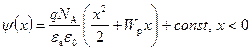. (2.49)

Используя граничные условия 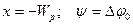, находим константу интегрирования:

.

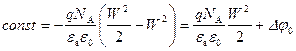Подставляя полученные значения константы в соотношение (2.49), получаем для распределения потенциала y (x) в области x < 0.

.

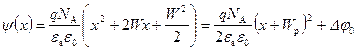Проводя аналогичное интегрировнаие для области x > 0, получаем:

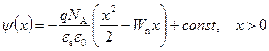. (2.50)

Используя граничные условия 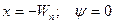; для константы интегрирования в этой области получаем:

,

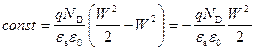Подставляя полученные значения константы в соотношение (2.50), получаем для распределения потенциала y (x) в области x > 0:

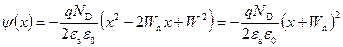. (2.51)

Таким образом, закон изменения потенциала y в p ‑области (отсчет идет от уровня в квазинейтральной области):

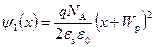, x < 0,

и наоборот, в n ‑области:

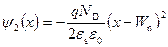, x > 0.

На рисунке 2.10 приведена диаграмма, иллюстрирующая распределение электрического поля и потенциала в p‑n переходе, рассчитанная по соотношениям (2.46), (2.47), (2.50) и (2.51).

Рис. 2.10. Диаграмма, иллюстрирующая распределение электрического поля и потенциала в p‑n переходе:

а) структура p‑n перехода; б) распределение электрического поля в ОПЗ; в) распределение потенциала в ОПЗ

На металлургической границе p‑n перехода при x = 0 значение потенциала y ₁ + y ₂ = D j ₀ = j _n0 + j _p0, или

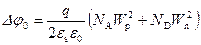. (2.52)

Согласно уравнению электронейтральности в замкнутых системах величины положительного и отрицательного заряда на единицу площади должны быть равны:

.

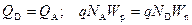Следовательно,

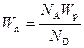. (2.53)

Подставляем выражение (2.45) в (2.46), получаем:

.

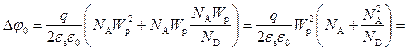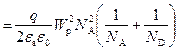
Несложные преобразования позволяют получить выражение для ширины обедненных областей W _p и W _n в p‑ и n ‑областях соответственно:

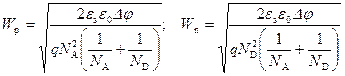. (2.54)

Из предыдущих формул легко видеть, что с ростом легирования p ‑области ширина p‑n перехода W _p в акцепторной части полупроводника уменьшится.

Полная ширина p‑n перехода W, равная W = W _p + W _n, будет:

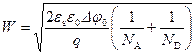. (2.55)

Для несимметричных p ⁺ ‑n переходов (концентрация акцепторов существенно больше концентрации доноров) из соотношений (2.47) и (2.48) следует, что ширина обедненной области в полупроводнике p ‑типа будет существенно меньше, чем ширина обедненной области в полупроводнике n ‑типа:

.

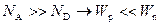Таким образом, вся обедненная область p ⁺ ‑n перехода сосредоточена в области с низким значением легирующей концентрации W = W _n.

2.11. Компоненты тока и квазиуровни Ферми в р‑n переходе

Рассмотрим токи в электронно‑дырочном переходе в равновесном (рис. 2.11) и неравновесном (при наличии внешнего напряжения, рис. 2.12) состоянии.

Рис. 2.11. Зонная диаграмма p‑n перехода, иллюстрирующая баланс токов в равновесном состоянии

В равновесном состоянии в p‑n переходе существуют четыре компоненты тока – две диффузионные и две дрейфовые. Диффузионные компоненты тока обусловлены основными носителями, дрейфовые – неосновными. В условиях термодинамического равновесия (V _G = 0) суммарный ток в p‑n переходе равен нулю, при этом диффузионные и дрейфовые компоненты попарно уравновешивают друг друга:

.

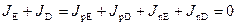При неравновесном состоянии если приложено прямое внешнее напряжение, то доминируют диффузионные компоненты, если приложено обратное напряжение, то доминируют дрейфовые компоненты.

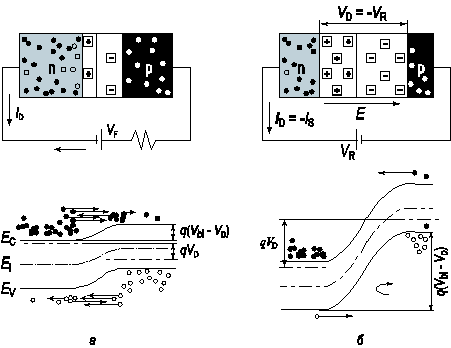
Рис. 2.12. Зонная диаграмма p‑n перехода, иллюстрирующая дисбаланс токов в неравновесном состоянии:

а) прямое смещение; б) обратное смещение

В неравновесных условиях область пространственного заряда p‑n перехода описывается двумя квазиуровнями Ферми – отдельно квазиуровнем Ферми для электронов F _n и отдельно для дырок F _p. При приложении внешнего напряжения расщепление квазиуровней Ферми F _n и F _p равно приложенному напряжению V _G [4, 3]. Пространственно область расщепления квазиуровней находится на расстоянии порядка диффузионной длины от металлургического p‑n перехода (рис. 2.13).

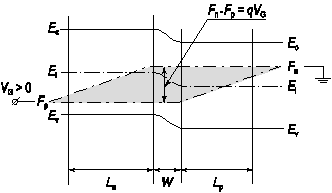
Рис. 2.13. Зонная диаграмма, иллюстрирующая расщепление квазиуровней Ферми F _n и F _p при приложении внешнего напряжения V _G > 0

Распределение концентрации неравновесных носителей в ОПЗ p‑n перехода и в квазинейтральном объеме будет отличаться от равновесного. На границе области пространственного заряда, где F _p - F _n = qV _G, выражение для концентрации n _n, p _n будет:

.

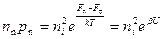В условиях низкого уровня инжекции концентрация основных носителей не меняется. Поэтому

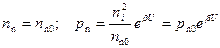. (2.56)

На рисунке 2.14 показано распределение основных и неосновных носителей в p‑n переходе в неравновесных условиях при прямом и обратном смещении.

Закон изменения неосновных неравновесных носителей, инжектированных в квазинейтральный объем, будет обсуждаться в следующем разделе. Здесь же обращаем внимание на то, что на границе с квазинейтральным объемом полупроводника концентрация неосновных носителей меняется в соответствии с уравнением (2.56), т.е. увеличивается при прямом смещении и уменьшается при обратном смещении.

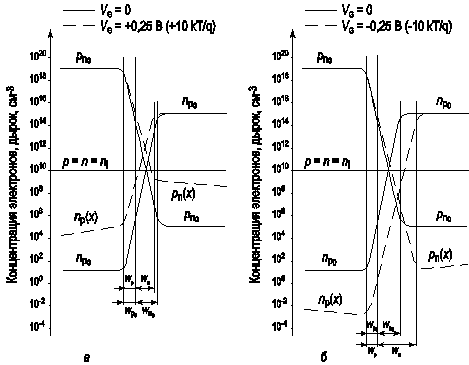
Рис. 2.14. Распределение основных и неосновных носителей в p‑n переходе в равновесном (сплошная линия) и неравновесном (пунктирная линия) состояниях

а) прямое смещение (V _G = +0,25 В); б) обратное смещение (V _G = -0,25 В)

2.12. Вольт‑амперная характеристика р‑n перехода

Получим вольт-амперную характеристику p‑n перехода. Для этого запишем уравнение непрерывности в общем виде:

.

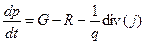Будем рассматривать стационарный случай .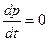

Рассмотрим ток в квазинейтральном объеме полупроводника n -типа справа от обедненной области p‑n перехода (x > 0). Темп генерации G в квазинейтральном объеме равен нулю: G = 0. Электрическое поле E тоже равно нулю: E = 0. Дрейфовая компонента тока также равна нулю: I _E = 0, следовательно, ток диффузионный 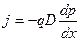. Темп рекомбинации R при малом уровне инжекции описывается соотношением:

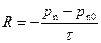. (2.57)

Воспользуемся следующим соотношением, связывающим коэффициент диффузии, длину диффузии и время жизни неосновных носителей: Dt = L _p².

С учетом отмеченных выше допущений уравнение непрерывности имеет вид:

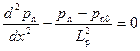. (2.58)

Граничные условия для диффузионного уравнения в p-n переходе имеют вид:

при x = 0, 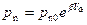; при x → ∞, . (*)

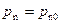Решение дифференциального уравнения (2.58) с граничными условиями (*) имеет вид:

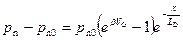. (2.59)

Соотношение (2.59) описывает закон распределения инжектированных дырок в квазинейтральном объеме полупроводника n ‑типа для электронно-дырочного перехода (рис. 2.15). В токе p‑n перехода принимают участие все носители, пересекшие границу ОПЗ с квазинейтральным объемом p‑n перехода. Поскольку весь ток диффузионный, подставляя (2.59) в выражение для тока, получаем (рис. 2.16):

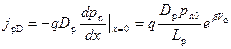. (2.60)

Соотношение (2.60) описывает диффузионную компоненту дырочного тока p‑n перехода, возникающую при инжекции неосновных носителей при прямом смещении. Для электронной компоненты тока p‑n перехода аналогично получаем:

.

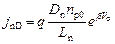При V _G = 0 дрейфовые и диффузионные компоненты уравновешивают друг друга. Следовательно, .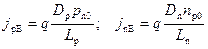

Полный ток p‑n перехода является суммой всех четырех компонент тока p‑n перехода:

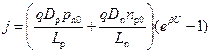. (2.61)

Выражение в скобках имеет физический смысл обратного тока p‑n перехода. Действительно, при отрицательных напряжениях V _G < 0 ток дрейфовый и обусловлен неосновными носителями. Все эти носители уходят из цилиндра длиной L _n со скоростью L _n/ t _p. Тогда для дрейфовой компоненты тока получаем:

.

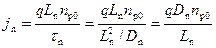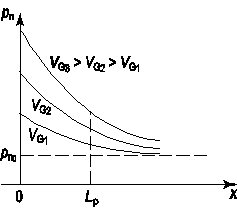
Рис. 2.15. Распределение неравновесных инжектированных из эмиттера носителей по квазинейтральному объему базы p‑n перехода

Нетрудно видеть, что это соотношение эквивалентно полученному ранее при анализе уравнения непрерывности.

Если требуется реализовать условие односторонней инжекции (например, только инжекции дырок), то из соотношения (2.61) следует, что нужно выбрать малое значение концентрации неосновных носителей n _p0 в p ‑области. Отсюда следует, что полупроводник p ‑типа должен быть сильно легирован по сравнению с полупроводником n ‑типа: N _A >> N _D. В этом случае в токе p‑n перехода будет доминировать дырочная компонента (рис. 2.16).

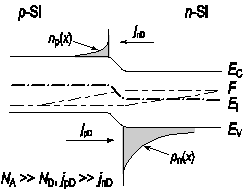
Рис. 2.16. Токи в несимметричном p‑n nереходе при прямом смещении

Таким образом, ВАХ p‑n перехода имеет вид:

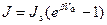. (2.62)

Плотность тока насыщения J _s равна:

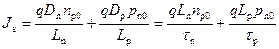. (2.63)

ВАХ p‑n перехода, описываемая соотношением (2.62), приведена на рисунке 2.17.

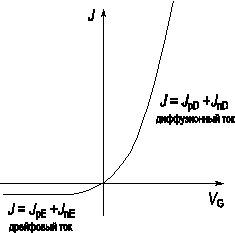
Рис. 2.17. Вольт‑амперная характеристика идеального p‑n перехода

Как следует из соотношения (2.16) и рисунка 2.17, вольт‑амперная характеристика идеального p‑n перехода имеет ярко выраженный несимметричный вид. В области прямых напряжений ток p‑n перехода диффузионный и экспоненциально возрастает с ростом приложенного напряжения. В области отрицательных напряжений ток p‑n перехода – дрейфовый и не зависит от приложенного напряжения.

Емкость p‑n перехода

Любая система, в которой при изменении потенциала j меняется электрический заряд Q, обладает емкостью. Величина емкости С определяется соотношением: .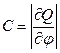

Для p‑n перехода можно выделить два типа зарядов: заряд в области пространственного заряда ионизованных доноров и акцепторов Q _B и заряд инжектированных носителей в базу из эмиттера Q _p. При различных смещениях на p‑n переходе при расчете емкости будет доминировать тот или иной заряд. В связи с этим для емкости p‑n перехода выделяют барьерную емкость C _B и диффузионную емкость C _D.

Барьерная емкость C _B – это емкость p‑n перехода при обратном смещении V _G < 0, обусловленная изменением заряда ионизованных доноров в области пространственного заряда.

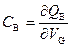. (2.64)

Величина заряда ионизованных доноров и акцепторов Q _B на единицу площади для несимметричного p‑n перехода равна:

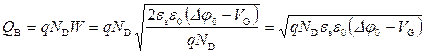. (2.65)

Дифференцируя выражение (2. 65), получаем:

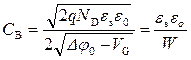. (2.66)

Из уравнения (2.66) следует, что барьерная емкость C _B представляет собой емкость плоского конденсатора, расстояние между обкладками которого равно ширине области пространственного заряда W. Поскольку ширина ОПЗ зависит от приложенного напряжения V _G, то и барьерная емкость также зависит от приложенного напряжения. Численные оценки величины барьерной емкости показывают, что ее значение составляет десятки или сотни пикофарад.

Диффузионная емкость C _D – это емкость p‑n перехода при прямом смещении V _G > 0, обусловленная изменением заряда Q _p инжектированных носителей в базу из эмиттера Q _p.

_,

,

.

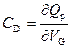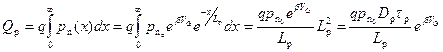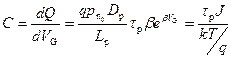Зависимость барьерной емкости С _B от приложенного обратного напряжения V _G используется для приборной реализации. Полупроводниковый диод, реализующий эту зависимость, называется варикапом. Максимальное значение емкости варикап имеет при нулевом напряжении V _G. При увеличении обратного смещения емкость варикапа уменьшается. Функциональная зависимость емкости варикапа от напряжения определяется профилем легирования базы варикапа. В случае однородного легирования емкость обратно пропорциональна корню из приложенного напряжения V _G. Задавая профиль легированияв базе варикапа N _D(x), можно получить различные зависимости емкости варикапа от напряжения C (V _G) – линейно убывающие, экспоненциально убывающие.

Date: 2015-05-05; view: 1162; Нарушение авторских прав