Как выяснить взаимное расположение прямых в пространстве?

Рассмотрим две прямые пространства:

– прямую 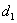, заданную точкой 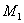и направляющим вектором ;
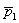– прямую 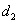, заданную точкой 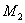и направляющим вектором .

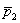Для лучшего понимания выполним схематический чертёж:

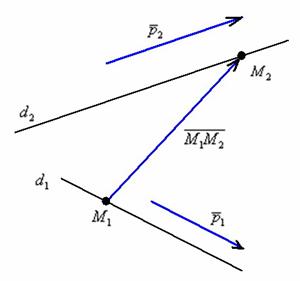
На чертеже в качестве примера изображены скрещивающиеся прямые.

Как разобраться с этими прямыми?

Так как известны точки 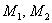, то легко найти вектор .

Если прямые скрещиваются, то векторы 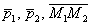не компланарны (см. урок Линейная (не) зависимость векторов. Базис векторов), а, значит, определитель, составленный из их координат, ненулевой. Или, что фактически то же самое, смешанное произведение векторов будет отлично от нуля: .

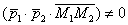В случаях №№2-4 наша конструкция «падает» в одну плоскость, при этом векторы 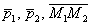компланарны, а смешанное произведение линейно зависимых векторов равняется нулю: .

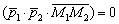Раскручиваем алгоритм дальше. Предположим, что , следовательно, прямые либо пересекаются, либо параллельны, либо совпадают.

Если направляющие векторы 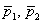не коллинеарны, то прямые пересекаются. Как проверить два вектора на коллинеарность, подробно рассмотрено в той же статье Линейная (не) зависимость векторов. Базис векторов.

Если направляющие векторы 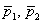коллинеарны, то прямые либо параллельны, либо совпадают. Финальным гвоздём предлагаю следующий приём: берём какую-либо точку одной прямой и подставляем её координаты в уравнение второй прямой; если координаты «подошли», то прямые совпадают, если «не подошли», то прямые параллельны.

Ход алгоритма незатейлив, но практические примеры всё равно не помешают:

Пример 11

Выяснить взаимное расположение двух прямых

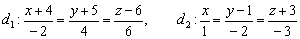
Решение: как и во многих задачах геометрии, решение удобно оформить по пунктам:

1) Вытаскиваем из уравнений точки и направляющие векторы:

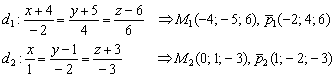
2) Найдём вектор: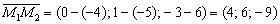

3) Вычислим смешанное произведение векторов:

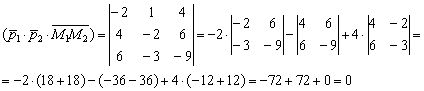
Таким образом, векторы 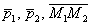компланарны, а значит, прямые 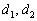лежат в одной плоскости и могут пересекаться, быть параллельными или совпадать.

4) Проверим направляющие векторы 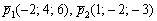на коллинеарность.

Составим систему из соответствующих координат данных векторов:

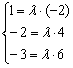
Из каждого уравнения следует, что 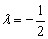, следовательно, система совместна, соответствующие координаты векторов пропорциональны, и векторы коллинеарны.

Вывод: прямые 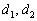параллельны либо совпадают.

5) Выясним, есть ли у прямых общие точки. Возьмём точку , принадлежащую первой прямой, и подставим её координаты в уравнения прямой :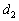

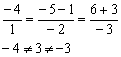
Таким образом, общих точек у прямых нет, и им ничего не остаётся, как быть параллельными.

Ответ: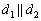

Интересный пример для самостоятельного решения:

Пример 12

Выяснить взаимное расположение прямых

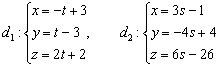
Это пример для самостоятельного решения. Обратите внимание, что у второй прямой в качестве параметра выступает буква 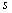. Логично. В общем случае – это же две различные прямые, поэтому у каждой прямой свой параметр.

И снова призываю не пропускать примеры, пороть буду предлагаемые мной задачи далеко не случайны;-)

Date: 2015-04-23; view: 1622; Нарушение авторских прав