Как найти уравнения прямой, содержащей общий перпендикуляр?

в) Эта задачка посложнее будет. Чайникам рекомендую пропустить данный пункт, не хочу охлаждать вашу искреннюю симпатию к аналитической геометрии =) Кстати, и более подготовленным читателям, возможно, лучше тоже повременить, дело в том, что по сложности пример надо бы поставить последним в статье, но по логике изложения он должен располагаться здесь.

Итак, требуется найти уравнения прямой 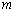, которая содержит общий перпендикуляр скрещивающихся прямых.

Общий перпендикуляр скрещивающихся прямых – это отрезок, соединяющий данные прямые и перпендикулярный данным прямым:

Вот наш красавец: 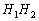– общий перпендикуляр скрещивающихся прямых 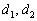. Он единственный. Другого такого нет. Нам же требуется составить уравнения прямой 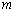, которая содержит данный отрезок.

Что известно о прямой «эм»? Известен её направляющий вектор 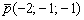, найденный в предыдущем пункте. Но, к сожалению, мы не знаем ни одной точки, принадлежащей прямой «эм», не знаем и концов перпендикуляра – точек 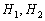. Где эта перпендикулярная прямая пересекает две исходные прямые? В Африке, в Антарктиде? Из первоначального обзора и анализа условия вообще не видно, как решать задачу…. Но есть хитрый ход, связанный с использованием параметрических уравнений прямой.

Решение оформим по пунктам:

1) Перепишем уравнения первой прямой в параметрической форме:

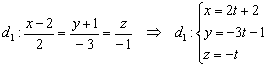
Рассмотрим точку 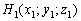. Координат мы не знаем. НО. Если точка принадлежит данной прямой, то её координатам 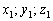соответствует вполне конкретное значение параметра, обозначим его через 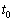. Тогда координаты точки запишутся в виде:

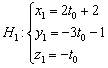
Или: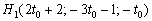

Жизнь налаживается, одна неизвестная – всё-таки не три неизвестных.

2) Такое же надругательство нужно осуществить над второй точкой. Перепишем уравнения второй прямой в параметрическом виде:

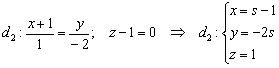
Если точка 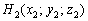принадлежит данной прямой, то при вполне конкретном значении 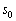её координаты должны удовлетворять параметрическим уравнениям:

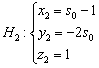
Или: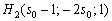

3) Вектор 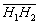, как и ранее найденный вектор 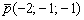, будет направляющим вектором прямой 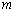. Как составить вектор по двум точкам, рассматривалось в незапамятные времена на уроке Векторы для чайников. Сейчас отличие состоит в том, что координаты векторов записаны с неизвестными значениям параметров. Ну и что? Никто же не запрещает из координат конца вектора вычесть соответствующие координаты начала вектора.

Есть две точки: .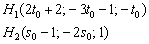

Находим вектор:

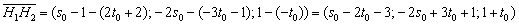
4) Поскольку направляющие векторы 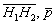коллинеарны, то один вектор линейно выражается через другой с некоторым коэффициентом пропорциональности «лямбда»:

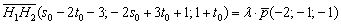
Или покоординатно:

Получилась самая, что ни на есть обычная система линейных уравнений с тремя неизвестными 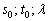, которая стандартно разрешима, например, методом Крамера. Но здесь есть возможность отделаться малой кровью, из третьего уравнения выразим «лямбду» и подставим её в первое и второе уравнение:

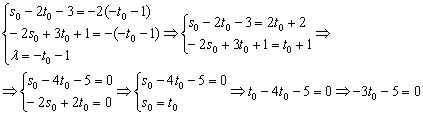
Таким образом: 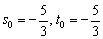, а «лямбда» нам не потребуется. То, что значения параметров получились одинаковыми – чистая случайность.

5) Небо полностью проясняется, подставим найденные значения 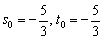в наши точки:

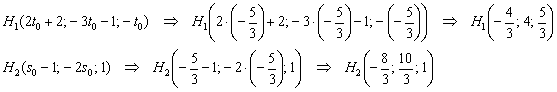
Направляющий вектор 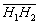особо не нужен, так как уже найден его коллега .

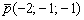После длинного пути всегда интересно выполнить проверку.

Подставим координаты точки 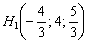в уравнения :

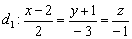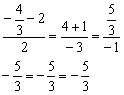
Получены верные равенства.

Подставим координаты точки 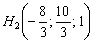в уравнения :

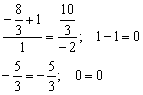
Получены верные равенства.

6) Заключительный аккорд: составим уравнения прямой 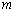по точке 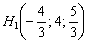(можно взять 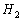) и направляющему вектору :

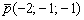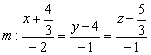
В принципе, можно подобрать «хорошую» точку с целыми координатами, но это уже косметика.

Date: 2015-04-23; view: 1253; Нарушение авторских прав