Поворот и параллельный перенос эллипса

Вернёмся к каноническому уравнению эллипса 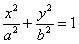, а именно, к условию 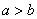, загадка которого терзает пытливые умы ещё со времён первого упоминания о данной кривой. Вот мы рассмотрели эллипс 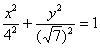, но разве на практике не может встретиться уравнение 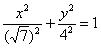? Ведь здесь 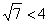, однако, это вроде бы как тоже эллипс!

Подобное уравнение нечасто, но действительно попадается. И оно действительно определяет эллипс. Развеем мистику:

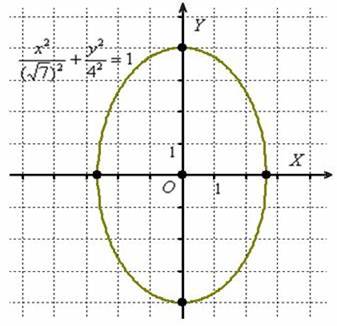
В результате построения получен наш родной эллипс, повёрнутый на 90 градусов. То есть, 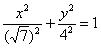– это неканоническая запись эллипса 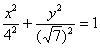. Запись! – уравнение 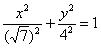не задаёт какой-то другой эллипс, поскольку на оси 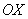не существует точек 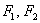(фокусов), которые бы удовлетворяли определению эллипса.

Как быть, если такое чудо-яйцо всё-таки встретилось на жизненном пути? В том случае если вам предложено построить эллипс, то, наверное, лучше построить его в нестандартном виде. С вершинами и дополнительными точками, думаю, трудностей не возникнет. Но если вам предложено найти фокусы, эксцентриситет и т.д., то настоятельно рекомендую начать (или продолжить после чертежа) решение так:

«Повернём эллипс на 90 градусов и перепишем его уравнение 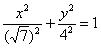в каноническом виде: 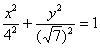» – дальше по обычной схеме.

! Примечание: в теории принято поворачивать не саму фигуру, а оси! И если от вас ТРЕБУЕТСЯ привести уравнение к каноническому виду, то решение, строго говоря, следует оформить иначе: «Перейдём к новой прямоугольной системе координат 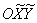, повернув координатные оси на 90 градусов против часовой стрелки, и запишем уравнение эллипса в каноническом виде: ».

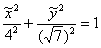Впрочем, эрудиты могут встать на скользкую дорожку путаницы, модифицировав все расчёты с учётом поворота. Но всё равно не советую. Потому что ребячество. Ведь эллипс можно повернуть и на другой угол =) Об этом мы ещё поговорим позже.

В практических задачах гораздо чаще встречается параллельный перенос эллипса:

Уравнение 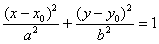задаёт эллипс с большой полуосью «а», малой полуосью «бэ» и центром симметрии в точке .

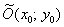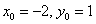Изобразим на чертеже эллипс . Согласно формуле: , то есть наш подопытный эллипс «переехал» в точку :

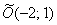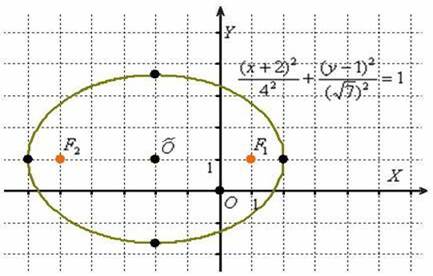
Значения 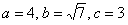остались прежними, а вот фокусы, разумеется, мигрировали, и формулы их координат придётся находить с поправкой на соответствующие сдвиги:

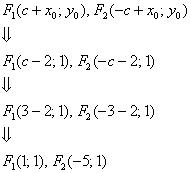
Здесь всё обходится значительно проще, чем при повороте, и если по условию не нужно приводить уравнение к каноническому виду, то лично я предпочту оставить его в виде . Что делать, если нужно приводить? «Чайникам» в большинстве случаев простят фразу: «Осуществим параллельный перенос эллипса в начало координат и перепишем уравнение в каноническом виде: 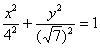». Но академический подход предполагает параллельный перенос не самой фигуры, а системы координат! Поэтому людям, изучающим высшую математику по профилю и/или углублённо, гораздо лучше завернуть примерно следующее: «С помощью параллельного переноса исходной системы координат перейдём к новой прямоугольной системе координат 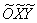с началом в точке 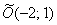и запишем уравнение эллипса в каноническом виде ».

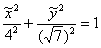На самом деле упрощенная версия формулы нам знакома ещё со школьных времён:

Уравнение 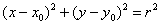задаёт окружность радиуса 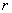с центром в точке .

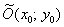Освежая ностальгические воспоминания, изобразим на чертеже окружность, заданную уравнением :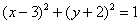

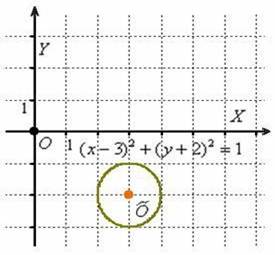
В исследовательских целях приведём наше уравнение к общему виду, выполнив возведение в квадрат и приведение подобных слагаемых:

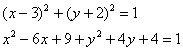
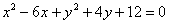– как правило, в таком обличье оно и встречается в природе.

Таким образом, в практических задачах часто предварительно нужно выполнить обратное действие – выделить полные квадраты. Данный приём подробно разобран на уроках о геометрических преобразованиях графиков и интегрировании дробей. Хотя следующий простой пример не должен вызвать у вас затруднений даже без отработки данного метода:

Пример 3

Построить график линии, заданной уравнением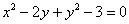

Решение и чертёж в конце урока.

На практике эллипс (как и другие линии) может быть одновременно повёрнут на любой угол относительно своего канонического положения и перенесен в любую точку, отличную от начала координат. В таком случае решается типовая задача приведения линии 2-го порядка к каноническому виду, к которой я потихоньку начал вас готовить уже сегодня.

Ну а пока самое время перейти ко второй части лекции, где жертвами станут гипербола и парабола.

Решения и ответы:

Пример 2: Решение: поскольку фокусы канонически расположенного эллипса имеют координаты 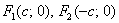, то расстояние от каждого из фокусов до начала координат равно: .
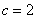По условию известно значение 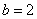, из соотношения 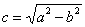находим:

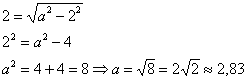
Запишем каноническое уравнение эллипса:

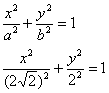
Вершины эллипса расположены в точках .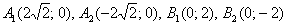
Найдём дополнительные точки:

Выполним чертёж:

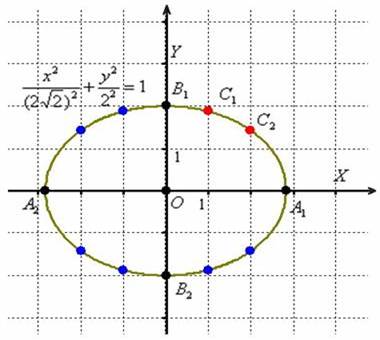
Вычислим эксцентриситет: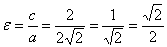

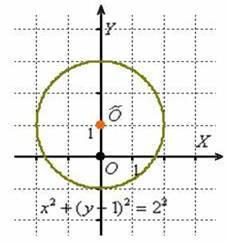
Пример 3: Решение: выделим полный квадрат:

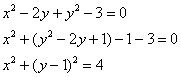
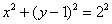– окружность радиуса 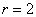с центром в точке .
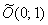Выполним чертёж:

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Гипербола и парабола

Переходим ко второй части статьи о линиях второго порядка, посвященной двум другим распространённым кривым – гиперболе и параболе. Если вы зашли на данную страницу с поисковика либо ещё не успели сориентироваться в теме, то рекомендую сначала изучить первый раздел урока, на котором мы рассмотрели не только основные теоретические моменты, но и познакомились с эллипсом. Остальным же читателям предлагаю существенно пополнить свои школьные знания о параболе и гиперболе. Гипербола и парабола – это просто? …Не дождётесь =)

Date: 2015-04-23; view: 3479; Нарушение авторских прав