Как найти точку пересечения двух прямых?

Если прямые 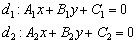пересекаются в точке 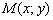, то её координаты являются решением системы линейных уравнений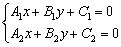

Как найти точку пересечения прямых? Решить систему.

Вот вам и геометрический смысл системы двух линейных уравнений с двумя неизвестными – это две пересекающиеся (чаще всего) прямые на плоскости.

Пример 4

Найти точку пересечения прямых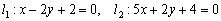

Решение: Существуют два способа решения – графический и аналитический.

Графический способ состоит в том, чтобы просто начертить данные прямые и узнать точку пересечения непосредственно из чертежа:

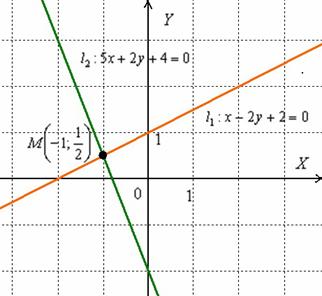
Вот наша точка: 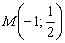. Для проверки следует подставить её координаты в каждое уравнение прямой, они должны подойти и там, и там. Иными словами, координаты точки 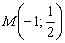являются решением системы 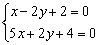. По сути, мы рассмотрели графический способ решения системы линейных уравнений с двумя уравнениями, двумя неизвестными.

Графический способ, конечно, неплох, но существует заметные минусы. Нет, дело не в том, что так решают семиклассники, дело в том, что на правильный и ТОЧНЫЙ чертёж уйдёт время. Кроме того, некоторые прямые построить не так-то просто, да и сама точка пересечения может находиться где-нибудь в тридесятом царстве за пределами тетрадного листа.

Поэтому точку пересечения 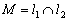целесообразнее искать аналитическим методом. Решим систему:

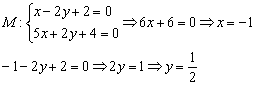
Для решения системы использован метод почленного сложения уравнений. Чтобы наработать соответствующие навыки, посетите урок Как решить систему уравнений?

Ответ: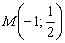

Проверка тривиальна – координаты точки пересечения должны удовлетворять каждому уравнению системы.

Пример 5

Найти точку пересечения прямых 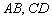в том случае, если они пересекаются.

Это пример для самостоятельного решения. Задачу удобно разбить на несколько этапов. Анализ условия подсказывает, что необходимо:
1) Составить уравнение прямой .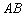
2) Составить уравнение прямой .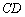
3) Выяснить взаимное расположение прямых .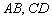
4) Если прямые пересекаются, то найти точку пересечения.

Разработка алгоритма действий типична для многих геометрических задач, и я на этом буду неоднократно заострять внимание.

Полное решение и ответ в конце урока:

Ещё не стоптана и пара башмаков, как мы подобрались ко второму разделу урока:

Date: 2015-04-23; view: 1825; Нарушение авторских прав