
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Термодинамические потенциалы. Все расчеты в термодинамике основываются на использовании функций состояния, называемых термодинамическими потенциалами
|
|
Все расчеты в термодинамике основываются на использовании функций состояния, называемых термодинамическими потенциалами. Каждому набору независимых параметров соответствует свой термодинамический потенциал. Изменения потенциалов, происходящие в ходе каких-либо процессов, определяют либо совершаемую системой работу, либо получаемое системой тепло.
При рассмотрении термодинамических потенциалов мы будем пользоваться соотношением
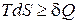 . (1.115)
. (1.115)
Знак равенства относится к обратимым, знак неравенства - к необратимым процессам.
Термодинамические потенциалы являются функциями состояния. Поэтому приращение любого из потенциалов равно полному дифференциалу функции, которой он выражается. Полный дифференциал функции f(x, у) переменных х и у определяется выражением
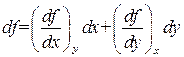 .
.
Поэтому, если в ходе преобразований мы получим для приращения некоторой величины выражение вида
 , (1.116)
, (1.116)
можно утверждать, что эта величина является функцией параметров 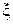 и
и 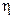 , причем функции
, причем функции 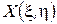 и
и  представляют собой частные производные функции
представляют собой частные производные функции 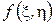 :
:
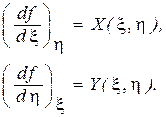 (1.117)
(1.117)
Внутренняя энергия. С одним из термодинамических потенциалов мы уже хорошо знакомы. Это — внутренняя энергия системы. Выражение первого начала для обратимого процесса можно представить в виде
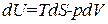 . (1.118)
. (1.118)
Сравнение с (1.116) показывает, что в качестве так называемых естественных переменных для потенциала U выступают переменные S и V. Из (1.117) следует, что
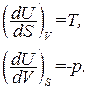 (1.119)
(1.119)
Из соотношений 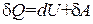 следует, что в случае, когда тело не обменивается теплом с внешней средой, совершаемая им работа равна
следует, что в случае, когда тело не обменивается теплом с внешней средой, совершаемая им работа равна
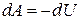 ,
,
или в интегральной форме:
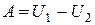 (нет теплообмена). (1.120)
(нет теплообмена). (1.120)
Таким образом, при отсутствии теплообмена с внешней средой работа равна убыли внутренней энергии тела.
При постоянном объеме
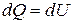 . (1.121)
. (1.121)
Следовательно, теплоемкость при постоянном объеме равна
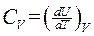 . (1.122)
. (1.122)
Свободная энергия. Согласно (1.118) работа, производимая телом при обратимом изотермическом процессе, может быть представлена в виде
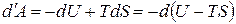 . (1.123)
. (1.123)
Функцию состояния
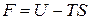 (1.124)
(1.124)
называют свободной энергией тела.
В соответствии с формулами (1.123) и (1.124) при обратимом изотермическом процессе работа равна убыли свободной энергии тела:
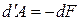 (1.125)
(1.125)
или
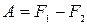 (T = const, обр.). (1.126)
(T = const, обр.). (1.126)
Сравнение с формулой (1.120) показывает, что при изотермических процессах свободная энергия играет такую же роль, как внутренняя энергия при адиабатических процессах.
Заметим, что формула (1.120) справедлива как при обратимых, так и при необратимых процессах. Формула же (1.126) справедлива только для обратимых процессов. При необратимых процессах δ Q<T dS (см. (1.115)). Подставив это неравенство в соотношение δ A= δ Q-dU, легко получить, что при необратимых изотермических процессах
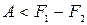 (T = const, необр.). (1.127)
(T = const, необр.). (1.127)
Следовательно, убыль свободной энергии определяет верхний предел количества работы, которую может совершить система при изотермическом процессе.
Возьмём дифференциал от функции (1.124). Приняв во внимание (1.118), получим
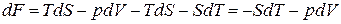 . (1.128)
. (1.128)
Из сравнения с (1.116) заключаем, что естественными переменными для свободной энергии являются Т и V. В соответствии с (1.117)
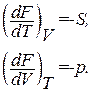 (1.129)
(1.129)
Заменим в (1.115) δ Q через dU + pdV и разделим получившееся соотношение на dt (t - время). В результате получим, что
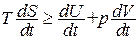 . (1.130)
. (1.130)
Если температура и объем остаются постоянными, то соотношение (1.130) может быть преобразовано к виду
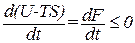
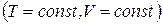 . (1.131)
. (1.131)
Из этой формулы следует, что необратимый процесс, протекающий при постоянных температуре и объеме, сопровождается уменьшением свободной энергии тела. По достижении равновесия F перестает меняться со временем. Таким образом, при неизменных Т и V равновесным является состояние, для которого свободная энергия минимальна.
Энтальпия. Если процесс происходит при постоянном давлении, то количество пoлyчaемого тепла можно представить следующим образом:
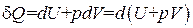 . (1.132)
. (1.132)
Функцию состояния
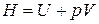 . (1.133)
. (1.133)
называют энтальпией или тепловой функцией.
Из (1.132) и (1.133) вытекает, что количество тепла, получаемого телом в ходе изобарического процесса, равно
δ Q=dH (1.134)
или в интегральной форме
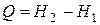 . (1.135)
. (1.135)
Следовательно, в случае, когда давление остается постоянным, количество получаемого телом тепла равно приращению энтальпии. Дифференцирование выражения (1.133) с учетом (1.118) дает
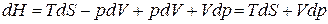 . (1.136)
. (1.136)
Отсюда заключаем, что энтальпия есть термодинамический потенциал в переменных S и р. Его частные производные равны:
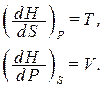 (1.137)
(1.137)
В соответствии с (1.134) теплоемкость при постоянном давлении равна
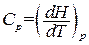 . (1.138)
. (1.138)
Сравнив формулы (1.134) и (1.138) с формулами (1.121) и (1.122), приходим к выводу, что при постоянном давлении энтальпия обладает свойствами, аналогичными тем, какие имеет внутренняя энергия при постоянном объеме.
Термодинамический потенциал Гиббса. Так называется функция состояния, определяемая следующим образом:
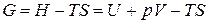 . (1.139)
. (1.139)
Ее полный дифференциал равен (см.(1.136))
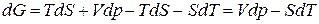 . (1.140)
. (1.140)
Следовательно, естественными переменными для функции G являются р и Т.
Частные производные этой функции равны:
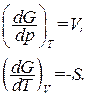 (1.141)
(1.141)
Если температура и давление остаются постоянными, соотношение (1.130) можно записать в виде
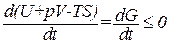
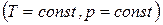 . (1.142)
. (1.142)
Из этой формулы следует, что необратимый процесс, протекающий при постоянных температуре и давлении, сопровождается уменьшением термодинамического потенциала Гиббса. По достижении равновесия G перестает изменяться со временем. Таким образом, при неизменных Т и р равновесным является состояние, для которого термодинамический потенциал Гиббса минимален (ср. с (1.131)).
В табл. 1.6 приведены основные свойства термодинамических потенциалов.
Таблица 1.6
| Название и обозначение термодинамического потенциала | Свойства |
Внутренняя энергия 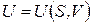
| 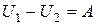 при адиабатическом процессе, при адиабатическом процессе,
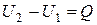 при V=const при V=const
|
Свободная энергия 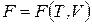
| 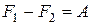 при обратимом изотермическом процессе при обратимом изотермическом процессе
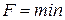 для равновесного состояния при T=const и p=const для равновесного состояния при T=const и p=const
|
Энтальпия 
| 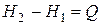 при p=const при p=const
|
Термодинамический потенциал Гиббса 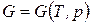
| 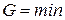 для равновесного состояния при T=const и p=const для равновесного состояния при T=const и p=const
|
Date: 2015-05-05; view: 1008; Нарушение авторских прав