Связь энтропии со статистическим весом. Свойства энтропии

В предыдущем параграфе мы установили, что вероятность макросостояния (в дальнейшем мы будем говорить просто – состояния) пропорциональна его статистическому весу Ω, т.е. числу микроскопических способов, которым может быть осуществлено данное макросостояние. Поэтому в качестве характеристики вероятности состояния можно было бы взять само это число, т.е. Ω. Однако такая характеристика не обладала бы свойством аддитивности. Чтобы убедиться в этом, разобьем данную систему на две практически не взаимодействующие подсистемы. Пусть эти подсистемы находятся в состояниях со статистическими весами Ω₁ и Ω₂. Число способов, которым может осуществляться соответствующее состояние системы, равно произведению чисел способов, которыми могут быть осуществлены состояния каждой из подсистем в отдельности:

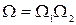. (1.88)

Отсюда следует, что Ω действительно не является аддитивной величиной.

Взяв логарифм от соотношения (21.1), получим

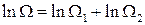. (1.89)

Из (1.89) видно, что – аддитивная величина. Иметь дело с аддитивными величинами много проще и удобнее. Поэтому в качестве характеристики вероятности состояния принимается величина 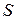, пропорциональная логарифму статистического веса. По причине, которая выяснится ниже, коэффициент пропорциональности выбирают равным постоянной Больцмана k. Определенную таким способом величину

. (1.90)

называют энтропией системы.

В рамках статистической физики будет показано, что энтропия, определенная с точки зрения термодинамики (п. 1.19) и энтропия, связанная со статистическим весом (1.90), представляет собой одну и ту же величину.

Из сказанного в предыдущем параграфе вытекают следующие свойства энтропии:

1. Энтропия изолированной системы при протекании необратимого процесса возрастает. Действительно, изолированная (т.е. предоставленная самой себе) система переходит из менее вероятных в более вероятные состояния, что сопровождается ростом величины (1.90).

2. Энтропия системы, находящейся в равновесном состоянии, максимальна.

3. Энтропия - величина аддитивная (то есть энтропия системы равна сумме энтропий подсистем).

Подчеркнем еще раз не абсолютно строгий характер высказанных утверждений. Например, энтропия системы, находящейся в равновесном состоянии, претерпевает незначительные кратковременные отрицательные флуктуации. Однако эти флуктуации столь малы, что практически энтропию можно считать постоянной и равной максимальному значению.

Утверждение о том, что энтропия изолированной системы может только возрастать (либо по достижении максимального значения оставаться неизменной), носит название закона возрастания энтропии или второго начала термодинамики. Иначе можно сказать, что энтропия изолированной системы не может убывать.

Итак, при протекании в изолированной системе необратимого процесса энтропия возрастает, т.е. выполняется соотношение

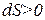. (1.91)

Date: 2015-05-05; view: 775; Нарушение авторских прав