Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Энтропия как функция состояния. Энтропия идеального газа
|
|
Величина S, определяемая соотношением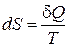 
(только для обратимых процессов), называется энтропией системы. Это понятие было введено в термодинамику Клаузиусом в середине XIX века.
Несмотря на то, что изменение количества теплоты зависит от процесса, энтропия является функцией состояния. Для необратимых процессов будет выполняться неравенство: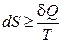 
. Интегрируя обе части полученного выражения получим неравенство, которое называется неравенством Клаузиуса: 
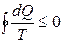, которое для квазистатических (процессов, состоящих из непрерывно следующих друг за другом равновесных состояний) процессов переходит в равенство 
.
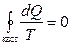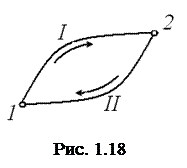Пусть система может переходить из начального состояния 1 (рис. 1.18) в конечное состояние 2 несколькими способами, каждый из которых является квазистатическим процессом. Возьмём два из них I и II. Эти процессы можно объединить в один квазистатический круговой процесс 1" I "2" II "1. Применим равенство Клаузиуса:
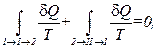или
или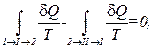, наконец,
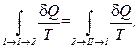(1.78)
Количество теплоты, полученное системой, делённое на абсолютную температуру Т, при которой оно было получено, иногда называют приведённым количеством теплоты. Величина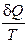 
есть элементарное приведённое количество теплоты, полученное в бесконечно малом процессе, а интеграл 
можно назвать приведённым количеством теплоты, полученным в конечном процессе. Тогда равенству Клаузиуса (1.78) можно дать следующую формулировку: приведённое количество теплоты, квазистатически полученное системой, не зависит от пути перехода, а определяется лишь начальным и конечным положениями системы. Этот результат позволяет ввести новую функции состояния – энтропию. То есть энтропия – функция состояния.
Рассчитаем энтропию идеального газа. Для этого используем первое начало термодинамики:
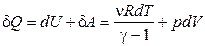. (1.79)
Подставим (1.79) в выражение, определяющее энтропию:
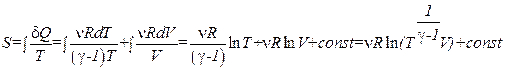. (1.80)
Это равенство также доказывает, что энтропия – функция состояния, поскольку при выводе не было сделано никаких предположений по поводу происходящего в системе процесса.
Date: 2015-05-05; view: 1081; Нарушение авторских прав