
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Характеристики турбины
|
|
Под характеристикой турбины турбобура принято понимать зависимость момента, мощности, перепада давления и коэффициента полезного действия от числа оборотов вала турбины при фиксированном расходе промывочной жидкости.
По способу получения характеристики турбин делятся на теоретические и экспериментальные.
Теоретические характеристики получают на основе формул, описывающих поведение указанных параметров турбины в функции числа оборотов вала при фиксированном расходе жидкости.
Экспериментальные характеристики получают на специальных стендах посредством испытаний 5 – 8 ступеней турбины с последующим пересчетом полученных результатов либо на одну ступень, либо на турбину в целом.
Остановимся на теоретических характеристиках турбин. Для этого обратимся к уравнению Л. Эйлера, представленному формулами (12) и (13) и к планам скоростей для входа и выхода из ротора (рис. 3.).
 |
Рис. 3. Планы скоростей: а) – для входа в ротор; б) – для выхода из ротора.
Используя планы скоростей, (рис. 3.) выразим окружные составляющие абсолютных скоростей c 1u и c 2u:
c 1u= c z·ctg α 1; c 2u= u - c z·ctg β 2. (27)
Подставив полученные выражения для окружных составляющих согласно (27) в уравнение момента (12) получим:
M i = ρ·Q [ c z·ctg α 1-(u - c z·ctg β 2)] r ср.= ρ·Q [ c z(ctg α 1+ ctg β 2) - u ] r ср=
= ρ·Q (u max- u) r ср, (28)
где c z(ctg α 1+ ctg β 2)= u max т. к. при полностью разгруженной турбине M i = 0, но ρ, Q и r ср не равны нулю, следовательно должна быть равна нулю разность, стоящая в квадратных скобках, а последнее возможно при u = u max.
Выразив в уравнении (28) окружную скорость через число оборотов, выраженное n мин-1, и памятуя, что u = 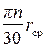 , получим:
, получим:
M i= ρ·Q (n max- n)  = ρ·Q·a м(n max- n), (28а)
= ρ·Q·a м(n max- n), (28а)
где a м=  - коэффициент момента.
- коэффициент момента.
Следовательно, зависимость момента от числа оборотов линейная, но из-за наличия дискового трения эта зависимость имеет некоторое отклонение от линейной.
Величина дискового трения может быть найдена по формуле:
M д= ρ·g·λ·n 2· D 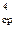 · l,
· l,
где λ – коэффициент трения (при работе на воде λ =0,52 – 0,54).
Анализируя уравнение (28а) видно, что при n =0 момент на валу имеет максимальное значение M i max= ρ·Q·a м· n max, а при n= n max M i=0.
Из уравнения (28) легко получить уравнение мощности ступени турбины:
N i= M i· ω = ρ·Q (u max- u) r ср· ω = ρ·Q (u max- u) u = ρ·Q·a n(n max- n) n, (29)
где a n= 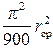 - коэффициент мощности.
- коэффициент мощности.
Уравнение (29) представляет собой уравнение параболы. Падение мощности слева и справа от экстремального режима обусловлено потерями на удар.
Определим экстремальное число оборотов. Для этого возьмём производную от уравнения (29) и приравняем её к нулю:
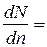 ρ·Q·a n(n max-2 n э)=0.
ρ·Q·a n(n max-2 n э)=0.
Поскольку ρ, Q и a n не равны нулю, то от сюда следует, что нулю может быть равна только разность, стоящая в скобках и, следовательно, n э= 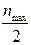 .
.
Тогда максимальная величина мощности будет равна:
N max= ρ·Q·a n 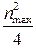 . (30)
. (30)
Известно, что коэффициент циркуляции определяют по формуле:
σ= 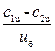 =
= 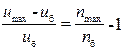 ; откуда
; откуда 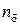 =
= 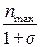 .
.
Следовательно, безударный режим у низкоциркулятивных турбин расположен справа от экстремального, т.к. σ <1. Если σ> 1, то безударный режим находится слева от экстремального; при σ =1 безударный и экстремальный режимы совпадают.
Рассмотрим поведение линии перепада давления.
Общий перепад давления Δ p о в ступени турбины можно разделить на три составляющие: перепад Δ p i, затрачиваемый на совершение полезной работы; перепад давления Δ p iб, затраченный на удар при «безударном режиме» и перепад давления на удар Δ p i уд при режиме отличном от безударного.
Перепад Δ p i, затрачиваемый на совершение полезной работы может быть найден с использованием уравнения напора турбины (16). Для этого правую и левую части этого уравнения умножим на ρ·g:
 ρ·g· H i=Δ p i=
ρ·g· H i=Δ p i= 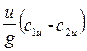 · ρ·g = ρ
· ρ·g = ρ 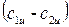 ·u = ρ · a н(n max- n) ·n, (31)
·u = ρ · a н(n max- n) ·n, (31)
где a Н – коэффициент напора, a Н = 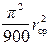 .
.
Левая часть выражения (31) представляет перепад давления. Не трудно видеть, что максимальная величина перепада давления будет аналогично мощности при n э= 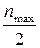 , а его максимальная величина будет равна:
, а его максимальная величина будет равна:
Δ p i max= ρ·a Н 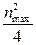 , (32)
, (32)
Перепад давления, затраченный на удар при «безударном режиме» Δ p iб минимален и он образуется из-за постоянства конструктивных углов лопаток вдоль длины.
Перепад давления на удар, при режиме отличном от безударного Δ p i уд, вычисляют по формуле:
Δ p i уд= ρ·b 1(2)· a Н(n-n б)2,
где b 1(2) – коэффициент, величина которого различна для левой и правой частей характеристики.
Таким образом, общие потери давления в ступени составят:
Δ p о= ρ · a н(n max- n) ·n + Δ p i б+ ρ·b 1,(2)· a Н(n-n б)2. (33)
Разделив почленно правую и левую части уравнения (33) на максимальный перепад давления, описываемый уравнением (32), получим перепад давления в турбине в безразмерной форме:
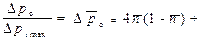
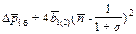 , (34)
, (34)
где 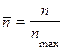 ,
, 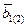 =
= 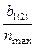 - безразмерные параметры.
- безразмерные параметры.
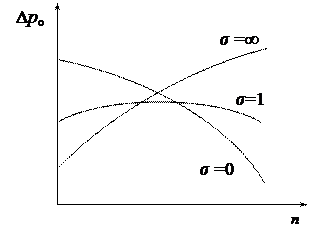
|
 Уравнение (34) есть уравнение линии перепада давления в безразмерной форме.
Уравнение (34) есть уравнение линии перепада давления в безразмерной форме.
Рис. 4. Зависимость перепада
давления от частоты вращения
ротора турбины.
 |
Рассмотрим поведение коэффициента полезного действия турбины.
Известно, что коэффициент полезного действия η есть отношение полезной мощности N п к затраченной N з:
η = 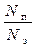 . (35)
. (35)
Значение полезной мощности нами было уже получено ранее в виде уравнения (29).
Величину затраченной мощности получим, умножив правую и левую часть уравнения (33) на расход жидкости Q:
N з= Δ p о· Q = Q [ ρ · a н(n max- n) ·n + Δ p i б+ ρ·b 1,(2)· a Н(n-n б)2]. (36)
Подставив в уравнение (35) значения числителя и знаменателя соответственно по уравнениям (29) и (36), получим:
η = 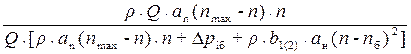 =
=
= 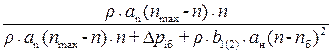 . (37)
. (37)
Разделив числитель и знаменатель уравнения (37) на максимальный перепад давления, описываемый выражением (32), получим:

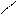

|
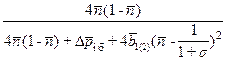 . (38)
. (38)

3.9. Характеристика «турбобур-долото-забой» (ТДЗ).
Действительная характеристика существенно отличается от характеристики турбины, поскольку турбобур содержит радиальные опоры и узел осевой опоры. Кроме того, в процессе бурения на вал турбобура действует сила реакции забоя, обусловленная осевой нагрузкой на долото и момент сил сопротивления вращению долота. Указанная сила и момент на вращение долота суммируются с внутренними силами и моментами, образующимися в турбине в процессе преобразования гидравлической энергии в механическую и, таким образом, формируют внешнюю характеристику гидравлического забойного двигателя.
Рассмотрим более подробно силы, действующие на вал ГЗД. Основные силы направлены вдоль оси вала. К ним относится сила, обусловленная весом всей вращающейся системы (с учетом Архимедовых сил) и направленная вниз, гидравлическая сила, обусловленная перепадом давления на роторах и статорах ступеней турбины и по направлению совпадающая с силой тяжести.
При бурении возникает третья сила, обусловленная реакцией забоя и направленная в противоположную сторону по отношению к первым двум силам. Результирующая сила, равная алгебраической сумме перечисленных трёх сил, передаётся осевой опоре, а от неё – бурильной колонне.

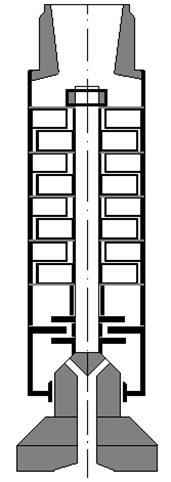 Рис. 6. Принципиальная схема турбобура.
Рис. 6. Принципиальная схема турбобура.
Составим уравнение равновесия осевых сил, приложенных к валу ГЗД в процессе бурения.
G + T – R=P, (39)
где G - вес вращающейся системы с учетом Архимедовых сил; T - гидравлическая сила; R – реакция забоя; P – сила, передаваемая на осевую опору.
К валу ГЗД приложены следующие моменты: момент, вырабатываемый турбиной М к, момент сил трения в радиальных опорах М р.о., момент сил трения в элементах осевой опоры М о.о. и момент сил сопротивления вращению долота М д.
Следовательно, уравнение моментов будет иметь вид:
М д= М к – М р.о. – М п. (40)
Представив момент на долоте в виде М д= М у· R и отбросив момент в радиальных опорах М р.о. в виду его малости (в сравнении с другими моментами), уравнение (40) примет вид:
М у· R = М к – М п. (41)
Момент в осевой опоре представим в виде:
М п.= P·μ·r пр= ± (G + T – R) μ·r пр, (42)
где μ – коэффициент трения; r пр – приведенный радиус трения, r пр= 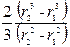 .
.
Подставим в уравнение (41) значение момента сил трения в осевой опоре в соответствии с уравнением (42):
М у· R = М к ± (G + T – R) μ·r пр (43)
Проведем преобразования в уравнении (43), записав его в виде:
М у· R ± R· μ·r пр = М к ± (G + T) μ·r пр,
R (М у ± μ·r пр)= М к ± (G + T) μ·r пр (44)
Уравнение (44) запишем в виде:
R = 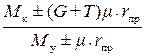 (45)
(45)
Умножив правую и левую части уравнения (45) на М у, а так же принимая во внимание линейную зависимость момента турбины М к от числа оборотов, получим:
R · М у= М д= 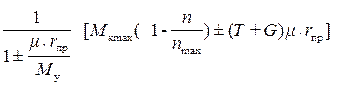 (46)
(46)
Обозначив отношение 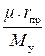 = φ и разделив обе части уравнения (46) на
= φ и разделив обе части уравнения (46) на 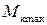 , получим:
, получим:
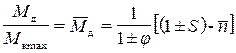 , (47)
, (47)
где S = [ 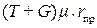 ] ∕
] ∕ 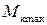 .
.
Уравнение (47) представляет зависимость момента на долоте от числа оборотов долота, представленное в безразмерной форме.
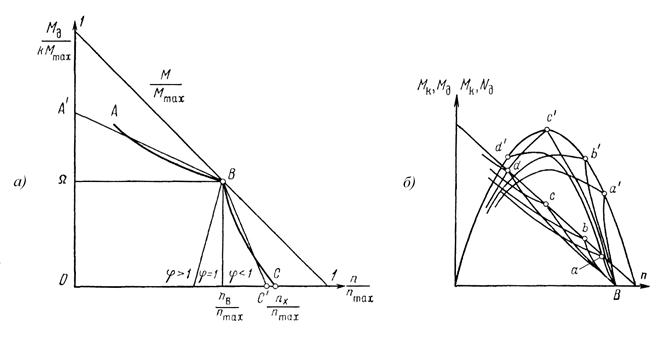
Рис. 3.6. Внешняя характеристика турбобура
а) – зависимость момента 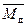 на долоте от числа оборотов долота
на долоте от числа оборотов долота 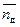 ;
;
б) - зависимость момента 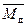 и мощности
и мощности 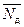 на долоте от числа оборотов долота
на долоте от числа оборотов долота 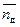 .
.
Date: 2015-05-05; view: 1532; Нарушение авторских прав
 n
n