Макроскопическое состояние. Термодинамические функции состояния. Уравнение состояния. Внутренняя энергия. Интенсивные и экстенсивные параметры

макроскопическое состояние-(макросостояние) системы, определяется значениями её термодинамических параметров: давления р, температуры Т, удельного объёма v, внутренней энергии U и т. п. Для определения макроскопического состояния однокомпонентной, однофазной системы достаточно знать значения любых 2 независимых параметров (например, Т и р или Т и v).

Функция состояния в термодинамике — функция независимых параметров, определяющих равновесное состояние термодинамической системы; не зависит от пути (характера процесса), следуя которому система пришла в рассматриваемое равновесное состояние (т.е. не зависит от предыстории системы); к функциям состояния относят, в частности, характеристические функции системы:

внутренняя энергия;

энтропия;

энтальпия и др.

Термодинамическая работа и количество теплоты не являются функциями состояния, так как их значение определяется видом процесса, в результате которого система изменила своё состояние.

Уравнение состояния идеального газа. Изопроцессы

Соотношение p = nkT, связывающее давление газа с его температурой и концентрацией молекул, получено в §3.2 для модели идеального газа, молекулы которого взаимодействуют между собой и со стенками сосуда только во время упругих столкновений. Это соотношение может быть записано в другой форме, устанавливающей связь между макроскопическими параметрами газа – объемом V, давлением p, температурой T и количеством вещества ν. Для этого нужно использовать равенства

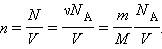
Здесь N – число молекул в сосуде, NА – постоянная Авогадро, m – масса газа в сосуде, M – молярная масса газа. В итоге получим:

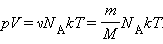
Произведение постоянной Авогадро NА на постоянную Больцмана k называется универсальной газовой постоянной и обозначается буквой R. Ее численное значение в СИ есть: R = 8,31 Дж/моль·К.

Соотношение

(*)

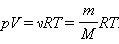называется уравнением состояния идеального газа.

Для одного моля любого газа это соотношение принимает вид: pV=RT.

Если температура газа равна Tн = 273,15 К (0 °С), а давление pн = 1 атм = 1,013·105 Па, то говорят, что газ находится при нормальных условиях. Как следует из уравнения состояния идеального газа, один моль любого газа при нормальных условиях занимает один и тот же объем V0, равный V0 = 0,0224 м3/моль = 22,4 дм3/моль.

Это утверждение называется законом Авогадро.

Для смеси невзаимодействующих газов уравнение состояния принимает вид pV = (ν1 + ν2 + ν3 +...)RT,

где ν1, ν2, ν3 и т. д. – количество вещества каждого из газов в смеси.

Уравнение, устанавливающее связь между давлением, объемом и температурой газа было получено в середине XIX века французским физиком Б. Клапейроном, в форме (*) оно было впервые записано Д. И. Менделеевым. Поэтому уравнение состояния газа называется уравнением Клапейрона–Менделеева.

Следует отметить, что задолго до того, как уравнение состояния идеального газа было теоретически получено на основе молекулярно-кинетической модели, закономерности поведения газов в различных условиях были хорошо изучены экспериментально. Поэтому уравнение (*) можно рассматривать как обобщение опытных фактов, которые находят объяснение в молекулярно-кинетической теории.

ВНУТРЕННЯЯ ЭНЕРГИЯ

термодинамич. ф-ция состояния системы, ее энергия, определяемая внутр. состоянием. В. э. складывается в осн. из кинетич. энергии движения частиц (атомов, молекул, ионов, электронов) и энергии взаимод. между ними (внутри- и межмолекулярной). На В. э. влияет изменение внутр. состояния системы под действием внеш. поля; во В. э. входит, в частности, энергия, связанная с поляризацией диэлектрика во внеш. электрич. поле и намагничиванием парамагнетика во внеш. магн. поле. Кинетич. энергия системы как целого и потенциальная энергия, обусловленная пространств. расположением системы, во В. э. не включаются. В термодинамике определяется лишь изменение В. э. в разл. процессах. Поэтому В. э. задают с точностью до нек-рого постоянного слагаемого, зависящего от энергии, принятой за нуль отсчета.

В. э. Uкак ф-ция состояния вводится первым началом термодинамики, согласно к-рому разность между теплотой Q, переданной системе, и работой W, совершаемой системой, зависит только от начального и конечного состояний системы и не зависит от пути перехода, т. е. представляет изменение ф-ции состояния

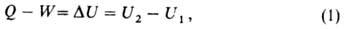
где U1 и 2 - В. э. системы в начальном и конечном состояниях соответственно. Ур-ние (1) выражает закон сохранения энергии в применении к термодинамич. процессам, т. е. процессам, в к-рых происходит передача теплоты. Для циклич. процесса, возвращающего систему в начальное состояние,. В изохорных процессах, т. е. процессах при постоянном объеме, система не совершает работы за счет расширения, W=0 и теплота, переданная системе, равна приращению В. э.: v=. > Для адиабатич. процессов, когда Q= 0, ∆U= - W.

В. э. системы как ф-ция ее энтропии S, объема V и числа молей mi i-того компонента представляет собой термодинамический потенциал. Это является следствием первого и второго начал термодинамики и выражается соотношением:

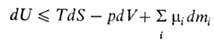
где Т - абс. т-ра, р- давление, -хим. потенциал i-того компонента. Знак равенства относится к равновесным процессам, знак неравенства-к неравновесным. Для системы с заданными значениями S, V,mi (закрытая система в жесткой адиабатной оболочке) В. э. при равновесии минимальна. Убыль В. э. в обратимых процессах при постоянных Vи Sравна макс. полезной работе (см. Максимальная работа реакции).

Зависимость В. э. равновесной системы от т-ры и объема U =f(T, V)наз. калорическим уравнением состояния. Производная В. э. по т-ре при постоянном объеме равна изохорной теплоемкости:

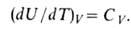
В. э. идеального газа от объема не зависит и определяется только т-рой.

Экспериментально определяют значение В. э. в-ва, отсчитываемое от ее значения при абс. нуле т-ры. Определение В. э. требует данных о теплоемкости С V (Т),> теплотах фазовых переходов, об ур-нии состояния. Изменение В. э. при хим. р-циях (в частности, стандартная В. э. образования в-ва) определяется по данным о тепловых эффектах р-ций, а также по спектральным данным. Теоретич. расчет В. э. осуществляется методами статистич. термодинамики, к-рая определяет В. э. как среднюю энергию системы в заданных условиях изоляции (напр., при заданных Т, V,mi). В. э. одноатомного идеального газа складывается из средней энергии поступат. движения молекул и средней энергии возбужденных электронных состояний; для двух- и многоатомных газов к этому значению добавляется также средняя энергия вращения молекул и их колебаний около положения равновесия. В. э. 1 моля одноатомного идеального газа при т-рах порядка сотен К составляет 3RT/2, где R-газовая постоянная; она сводится к средней энергии поступат. движения молекул. Для двухатомного газа мольное значение В. э.-ок. 5RT/2 (сумма поступат. и вращат. вкладов). Указанные значения отвечают закону равнораспределения энергии для названных видов движения и вытекают из законов классич. статистич. механики. Расчет колебат. и электронного вкладов во В. э., а также вращат. вклада при низких т-рах требует учета квантовомех. закономерностей. В. э. реальных систем включает помимо вкладов, учитываемых для идеального газа, также среднюю энергию межмолекулярных взаимодействии.

"Термодинамическое состояние — это состояние вещества с точки зрения его давления, температуры, внутренней энергии, плотности, удельного объема, энтальпии и энтропии. Любые два параметра вещества определяют его термодинамическое состояние. Существует две категории термодинамических параметров: интенсивные и экстенсивные. Интенсивный параметр — это свойство, которое не зависит от количества или размера системы. Температура и давление — интенсивные параметры веществ и систем. Экстенсивные параметры зависят от количества или размера вещества или системы. Масса и объем — экстенсивные параметры."