
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Полярная система координат
|
|
Полярная система координат на плоскости определяется заданием некоторой точки О, называемой полюсом, луча  , исходящего из этой точки и называемого полярной осью, и единицы масштаба
, исходящего из этой точки и называемого полярной осью, и единицы масштаба 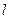 (рис. 4.10).
(рис. 4.10).
Пусть М – произвольная точка плоскости. Обозначим 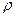 = ОМ – расстояние точки М от полюса,
= ОМ – расстояние точки М от полюса,  – угол, отсчитываемый от полярной оси против часовой стрелки до направления ОМ.
– угол, отсчитываемый от полярной оси против часовой стрелки до направления ОМ.
Числа 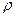 и
и  называются полярными координатами точки М,
называются полярными координатами точки М, 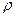 – полярный радиус,
– полярный радиус,  – полярный угол точки М.
– полярный угол точки М.
Задание пары чисел (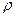 ,
,  ) однозначно определяет точку М на плоскости. Если ограничить изменение
) однозначно определяет точку М на плоскости. Если ограничить изменение  пределами
пределами  (или
(или 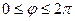 ), то каждой точке плоскости также будет однозначно соответствовать пара чисел (
), то каждой точке плоскости также будет однозначно соответствовать пара чисел (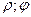 ).
).
Исключение составляет полюс, для которого 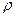 = 0, а угол
= 0, а угол  не определен.
не определен.

Рис. 4.10
Часто оказывается полезным рассматривать на плоскости полярную систему координат (ПСК) вместе с декартовой системой координат (ДСК). Выберем ДСК так, чтобы ее начало 0 совпадало с полюсом, а ось ОХ была направлена по полярной оси  (рис.4.11). Тогда полярные координаты (
(рис.4.11). Тогда полярные координаты (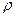 ,
,  ) и декартовы координаты (
) и декартовы координаты (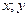 ) точки М связаны соотношениями:
) точки М связаны соотношениями:
 ; ; 
| (4.25) |

| (4.26) |
 (4.27)
(4.27)
Из этих формул следует:
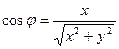 ; ; 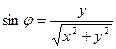
| (4.28) |

Рис. 4.11
Формула для 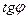 определяет два угла
определяет два угла  и
и  +
+  в промежутке [0; 2
в промежутке [0; 2  ). Чтобы уточнить, какой из углов выбрать, нужно учесть четверть, в которой находится точка М, или воспользоваться формулами (4.28).
). Чтобы уточнить, какой из углов выбрать, нужно учесть четверть, в которой находится точка М, или воспользоваться формулами (4.28).
Чтобы перейти от уравнения линии в декартовых координатах к ее полярному уравнению, нужно вместо (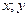 ), подставить в уравнение их выражения из формул (4.25). Обратный переход от полярного уравнения к уравнению в декартовых координатах осуществляется с помощью формул (4.26), (4.28).
), подставить в уравнение их выражения из формул (4.25). Обратный переход от полярного уравнения к уравнению в декартовых координатах осуществляется с помощью формул (4.26), (4.28).
Пример. Построить в полярной системе координат точки:

Решение. Построение точек показано на рис. 4.12.
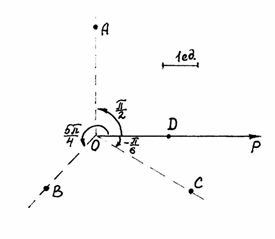
Рис. 4.12
Уравнение  , связывающее три переменные
, связывающее три переменные  , задает в пространстве некоторую поверхность
, задает в пространстве некоторую поверхность 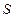 .
.
Основная задача: на основании некоторой информации о данной поверхности 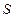 (обычно геометрического смысла) составить уравнение, которому удовлетворяют координаты любой точки поверхности
(обычно геометрического смысла) составить уравнение, которому удовлетворяют координаты любой точки поверхности 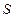 и только они.
и только они.
Рассмотрим простейшую поверхность – плоскость.
Date: 2015-05-04; view: 683; Нарушение авторских прав