Универсальная математическая модель ГТД

В работах [1,2,3,4,5,6,7] сделаны попытки сформулировать требования к математическим моделям ГТД. Наиболее полно на наш взгляд такие требования сформулированы в работе [7]. Они разделены на три группы. К первой группе относятся требования, обеспечивающие адекватность математических моделей, т.е. такие модели должны достаточно точно описывать рабочий процесс в проточной части ГТД. Ко второй группе относятся требования, обеспечивающие достаточную универсальность математической модели, т.е. возможность ее использования для решения широкого круга задач. К третьей группе относятся требования, обеспечивающие высокий уровень программирования. Ниже приведены эти требования, исправленные и дополненные по сравнению с [7].

Первая группа.

1. Учет изменения теплофизических свойств рабочего тела в зависимости от его состава и температуры, а в двигателях сложных схем и в зависимости от давления.

2. Учет влияния влажности воздуха, входящего в двигатель.

3. Учет влияния изменения состава и свойств рабочего тела, т.е. конденсации паров, диссоциации или, реже, ионизации газов.

4. Учет изменения полноты сгорания топлива, в особенности на больших высотах полета.

5. Возможность учета изменения состава и свойств рабочего тела при низких значениях коэффициента полноты сгорания.

6. Возможность использования любых заданных характеристик компрессоров с погрешностью не более 0.2...0.5%.

7. Возможность использования любых заданных характеристик турбин с погрешностью не более 0.2...0.5%.

8. Учет изменения коэффициентов потерь в узлах ГТД в зависимости от режима работы, характеризуемого различными параметрами.

9. Возможность учета радиальной неравномерности потока за вентилятором в ТРДД с большой степенью двухконтурности.

10. Возможность учета различий статического давления в газовых потоках внутреннего и наружного контуров на входе в камеру смешения.

11. Возможность учета влияния неравномерности и нестационарности потока на входе в узлы двигателя на характеристики этих узлов.

12. Возможность учета изменений в характеристиках узлов ГТД при изменении внешних условий.

13. Учет влияния числа Рейнольдса на коэффициенты потерь и характеристики узлов.

14. Учет затрат мощности на привод агрегатов и на механические потери каждого из валов в зависимости от режимов работы.

15. Учет влияния температуры деталей на изменение геометрических размеров проточной части.

16. Учет влияния упругой раскрутки длинных лопаток осевого компрессора на изменение его характеристики.

17. Возможность уточнения наименее достоверных параметров модели путем ее идентификации по результатам эксперимента.

Вторая группа.

18. Возможность расчета со сложными системами отбора воздуха за различными ступенями компрессоров, отбираемого как на охлаждение горячей части ГТД, так и безвозвратно на самолетные и другие нужды.

19. Возможность расчета со сложными системами подвода воздуха для охлаждения горячей части с учетом его влияния не только на температуру, но и на потери в потоке газа.

20. Возможность расчета при параметрах атмосферного воздуха, отличающихся от стандартных.

21. Универсальность, т.е. пригодность для ГТД большинства применяемых схем.

22. Возможность применения для ГТД с узлами различных типов.

23. Многорежимность, т.е. возможность расчета на любых реальных режимах работы ГТД.

24. Возможность расчета переходных процессов (приемистость, сброс оборотов).

25. Возможность расчета на глубоких нерасчетных режимах (малый газ, авторотация, реверс и т.п.).

26. Возможность расчета процесса запуска при заданной характеристике стартера.

27. Возможность реализации произвольных и сложных программ управления.

28. Универсальность применения, т.е. возможность решения широкого набора задач для данного двигателя.

29. Возможность изменения уровня сложности модели в целом или ее модулей, описывающих отдельные узлы ГТД.

30. Возможность расчета с различными топливами.

Третья группа.

31. Модульный принцип построения программы или программного комплекса.

32. Защищенность модели, т.е. возможность расчета при любых самых неблагоприятных сочетаниях входных данных без прерываний и аварийных остановов.

33. Применимость для САПР.

Трудностью при создании математических моделей проточной части ГТД (особенно многорежимных) является организация вычислительного процесса. Эта трудность заключается в том, что при расчете двигателей, особенно сложных схем необходимо ряд параметров задавать в нулевом приближении, т.к. их точное значение может быть определено только после завершения расчета. Но задание таких параметров в нулевом приближении приводит по окончании расчета по модели к различного рода рассогласованиям (невязкам). Так, например, при расчете высотно-скоростных характеристик двухконтурного, двухвального ТРД с нерегулируемыми проходными сечениями при законе управления Т_г^* = const, неизвестны заранее значения суммарного расхода воздуха G_Вå, частот вращения роторов n₁ и n₂, степени двухконтурности m, положение точек совместной работы компрессоров и, как следствие, неизвестны значения степени повышения давления и к.п.д. компрессоров, необходимые для расчета. Для того чтобы алгоритм расчета формально отработал, необходимо задать в нулевом приближении значения этих или других параметров, при помощи которых они могут быть определены.

После выполнения расчета с этими приближенными значениями параметров возникают невязки, характеризуемые отсутствием баланса мощностей на валах двигателя, баланса расходов газа через характерные сечения проточной части, отсутствием равенства статических давлений во входных сечениях камеры смешения (если она есть в двигателе). Возможны и другие невязки.

Возникает задача устранения невязок, т.е. обращение их в “ноль”, путем уточнения значений параметров, заданных в нулевом приближении. Известны три различных метода решения этой задачи.

1. Метод закольцовок (точнее метод вложенных итерационных циклов). Он заключается в том, что при получении первой невязки отличной от нуля, процесс расчета прерывается и организуется цикл, т.е. расчет повторяется с того момента, когда были заданы параметры в нулевом приближении. На каждом приближении значения этих параметров уточняются так, чтобы данная невязка обратилась в ноль. Применяются различные алгоритмы уточнения. При появлении второй невязки отличной от нуля, аналогично организуется второй цикл, причем внутри него будет находиться первый цикл. Аналогично организуются циклы и для всех последующих невязок.

2. Метод систем уравнений. Он заключается в том, что заранее составляется и программируется система уравнений. Каждое уравнение в этой системе обеспечивает равенство нулю одной из невязок, а искомыми неизвестными являются те параметры, которые задавались в нулевом приближении (варьируемые параметры).

3. Метод систем невязок. Он заключается в том, что, как и в первом методе, неизвестные значения параметров задаются в нулевом приближении, рассчитываются и запоминаются значения всех невязок. Отличие заключается в том, что циклы не организуются, а с помощью входных данных автоматически формируется необходимая система уравнений, аналогичная системе из второго метода, т.е. она не является заранее запрограммированной.

Из трех описанных методов первым стал применяться метод вложенных итерационных циклов и, несмотря на его недостатки, он до сих пор применяется в большинстве математических моделей ГТД. Основные его недостатки заключаются в том, что алгоритм становится чрезмерно громоздким в двигателях сложных схем, когда значительно возрастает количество невязок. Кроме того, его применение практически невозможно в универсальных математических моделях, рассчитанных на ГТД различных схем.

Из-за этих недостатков данный метод в настоящее время считается устаревшим. Его рекомендуется применять только в математических моделях ГТД простых схем и, если число схем невелико.

Методы систем уравнений и систем невязок близки между собой. В обоих случаях задача сводится к решению некоторой системы нелинейных, трансцендентных уравнений. Разница заключается только в том, что в одном случае система программируется заранее, а в другом формируется автоматически. Математические модели, в которых применяется метод систем уравнений, получаются более простыми. Они получили широкое распространение в промышленности [1,2,3]. Модели, базирующиеся на методе систем невязок, удается сделать более универсальными [4,11].

Во всех версиях программного комплекса ГРАД применяется метод систем невязок, т.к. требование универсальности было одним из основных при его создании.

Номенклатура варьируемых параметров и невязок задается с входными данными математической модели. Для каждого из варьируемых параметров задается адрес, по которому его значение находится во входных данных модели. Каждая невязка задается двумя адресами: один из них позволяет найти значение нужного параметра в массиве выходных данных модели, а второй значение параметра, которое нужно сопоставить с первым для получения невязки. Второй параметр может находиться как в числе выходных, так и входных данных модели.

1.1. Структура входной и выходной информации

Для удобства реализации выбранного метода организации вычислительного процесса вся входная и выходная информация математической модели сведена в единый информационный массив с идентификатором “А”. Он содержит все необходимые входные данные, в число которых входят различные константы модели, данные, описывающие конструктивную схему (определяющие последовательность расчета), входные данные, определяющие отдельные узлы двигателя (параметры узлов, характеристики узлов, информация об отборах и подводах воздуха или газа, информация о коррекции характеристик), входные данные, представляющие собой список варьируемых параметров и параметров, образующих невязки, список параметров, определяющих условия управления. По окончании расчета в этот же массив заносятся результаты расчета по модели.

Этот массив имеет строго определенную структуру. Условно он подразделяется на два подмассива, каждый из которых делится на группы. Группы первого подмассива содержат информацию по двигателю в целом. Группы второго подмассива содержат информацию по отдельным узлам двигателя, входящим в конструктивную схему. Эти группы дополнительно подразделяются на подгруппы, число которых может для разных узлов меняться от двух до пяти.

Первая подгруппа содержит входные параметры узла. Вторая - результаты расчета этого узла. Третья - его характеристики (точнее входные данные, описывающие характеристики). Четвертая - входные данные, описывающие отборы или (и) подводы воздуха (газа), производимые в данном узле. Пятая - входные данные, описывающие возможную коррекцию характеристик узла при его регулировании, модификации или любых других воздействиях.

Структура всех групп и подгрупп массива “А” одинаковая и имеет вид NG, Z, P₁, P₂,...,P_z-2,

где NG - условный номер группы, подгруппы,

Z - количество элементов в группе, включая условный номер,

P₁, P₂, P_z-2 - параметры группы (подгруппы).

Каждому элементу группы приводится в соответствие определенная позиция.

Так NG - нулевая позиция

Z - первая позиция

P₁ - вторая позиция

P₂ - третья позиция и т.д.

Подробно, структура и состав основного информационного массива математической модели, приведены в отдельном документе.

Такая организация входных и выходных данных обеспечивает не только удобную организацию вычислительного процесса, но и удобство адаптации модели к решению различных задач в произвольных постановках, особенно при решении задач идентификации математической модели (уточнения) по результатам испытаний двигателя, различного рода оптимизационных задач и при моделировании произвольных программ управления.

1.2. Структура универсальной математической модели ГТД

Схематично структуру универсальной математической модели можно представить, как иерархическую совокупность программных модулей. На вход внешнего модуля математической модели (подпрограмм “MODEL”) подается основной информационный массив “А” и ряд вспомогательных массивов (все они передаются через именованные общие области).

Модулями верхнего уровня на основе анализа поступивших входных данных организуется вычислительный процесс, включающий в себя организацию обращений в требуемой последовательности к модулям нижнего уровня (модуль “Двигатель” - модули узлов) с целью формирования системы уравнений, определяющих условия совместной работы узлов двигателя. Затем организуется процесс решения этой системы уравнений. В результате ее решения определяются параметры двигателя в одной режимной точке при заданных (через массив “А”) внешних условиях и условиях управления. Затем осуществляется выход из модели, с передачей управления внешнему обрабатывающему модулю, вызвавшему модель.

1.3. Алгоритм решения системы трансцендентных уравнений, определяющих

условия совместной работы узлов двигателя.

Как уже указывалось выше, в математической модели данного программного комплекса вычислительный процесс построен по методу невязок, т.е. в результате последовательного расчета модулей узлов (в соответствии с шифром схемы) и на основе анализа входных данных автоматически формируется система определяющих уравнений вида

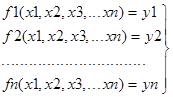(1.1)

Где f_j (j=1,2,...,n) - некоторые функции отличные от нуля на величину невязки y_j (j=1,2,...,n) вследствие приближенного задания значений независимых переменных (варьируемых параметров) x_i (i=1,2,...,n). В результате решения системы уравнений (1.1) требуется определить значения варьируемых параметров x_i, при которых невязки y_i обратились бы в ноль с заданной точностью. Для решения таких систем применяются различные математические методы. Хорошо зарекомендовал себя метод Ньютона и ряд его модификаций.

Опыт эксплуатации показал, что широко известный метод Ньютона и его модификации часто не обеспечивает решения данной системы, поэтому был разработан гибкий полиметод. Он включает в себя метод Ньютона-Рафсона. Основное усовершенствование метода заключается в следующем.

Вычисление матрицы Якоби осуществляется путем односторонней вариации по всем варьируемым параметрам "x" системы уравнений (1.1) с нормированием столбцов по формуле

x_i^' = x_0i + d_i m (x_maxi - x_mini), (1.2)

где x_0i - исходное значение варьируемого параметра;

x_i^' - значение варьируемого параметра после вариации;

x_maxi,x_mini - границы изменения варьируемого параметра;

m - масштаб вариации;

d_i - нормирующий коэффициент, первоначально принимаемый равным 1 и затем после вычисления элементов матрицы Якоби уточняемый по формуле

d_i = 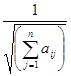_2, 1.3)

где 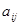- элементы матрицы Якоби.

А = 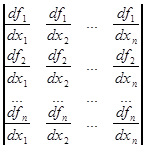(1.4)

Частные производные 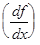_ij вычисляются численным методом по следующей формуле

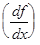_{ij = 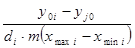.} (1.5)

Таким образом получаются матрица Якоби А и матрица нормирующих коэффициентов

D = 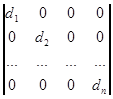(1.6)

В результате перемножения матриц А и D получается матрица N.

N = A×D (1.7)

После обращения матрицы N и умножения ее на вектор невязок в исходной точке получается искомый вектор приращений к варьируемым параметрам

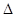X = N^-1×y₀ (1.8)

После чего определяются новые значения варьируемых параметров на данном приближении.

X_i = X_0i + 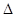X_i (1.9)

В процессе каждого приближения вдоль вектора, проходящего через точки x_0i и x_i, определяющего направление поиска решения, осуществляется линейный поиск лучшего значения нормированной суммы квадратов невязок

S = 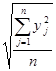, (1.10)

поэтому вместо уравнения (1.9) используется уравнение вида

X_i = X_0i + 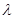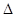X_i (1.11)

Линейный поиск сводится к поиску такого значения 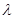, при котором бы функция S(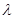) принимала минимальное значение.

Стратегия линейного поиска заключается в следующем. Вначале делается единичный шаг по уравнению (1.11) при 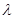=1 и если он удачен (произошло уменьшение S), то на этом приближение заканчивается. В случае неудачного шага (S 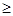S₀), осуществляется поиск наилучшей длины шага методом параболы (аппроксимация функции S (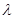) уравнением параболы с поиском его минимума), или методом Киффера (с использованием чисел Фибоначчи). Выбор того или другого метода осуществляется автоматически в зависимости от сложившейся ситуации в процессе поиска. В случае нулевых шагов ( 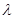= 0), что дает возможность предполагать наличие “овражной” ситуации, или “локального минимума” используется овражный алгоритм И.М.Гельфанда [10].

Кроме перечисленных усовершенствований предусмотрена возможность сохранения матрицы N^-1 текущего приближения, если оно оказалось удачным по темпу уменьшения S. В этом случае при расчете 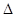X для последующего приближения по уравнению (1.8) вместо “y₀”, берется вектор невязок “y” полученный в процессе данного приближения.