Доход потребителя, цены и бюджетное ограничение потребителя

Однако предпочтения потребителя – это не единственный фактор, влияющий на его выбор. Существенное влияние на этот процесс оказывают также доход, которым располагает потребитель и цены, по которым он покупает товары на рынке. В совокупности эти два параметра определяются как бюджетное ограничение потребителя (consumer budget constraint).

Для упрощения, мы продолжаем пользоваться введенными ранее допущениями, ограничивая анализ двумя товарами, полагая, при этом, что доход потребителя (I), то есть сумма денег, доступная для расходования, постоянен в рассматриваемой нами перспективе. Мы также полагаем, что цены, то есть сумма денег, которую потребитель должен заплатить за единицу каждого товара (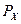 и 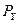), не зависят от потребителя. Графические построения мы будем выполнять в рамках того же товарного пространства.

Если потребитель потратит весь свой доход на приобретение товаров 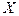и 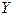, то его бюджетное ограничение можно выразить линейной функцией:

,

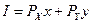где: 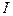– денежный доход потребителя; 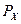, 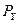– цены товаров 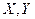, 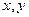– количество товаров .

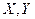Как известно, для построения графика линейной функции достаточно иметь две точки. Пусть это будут точки, в которых график нашей функции пересекает оси (Рис. 2.4.). Эти точки показывают, какое количество одного 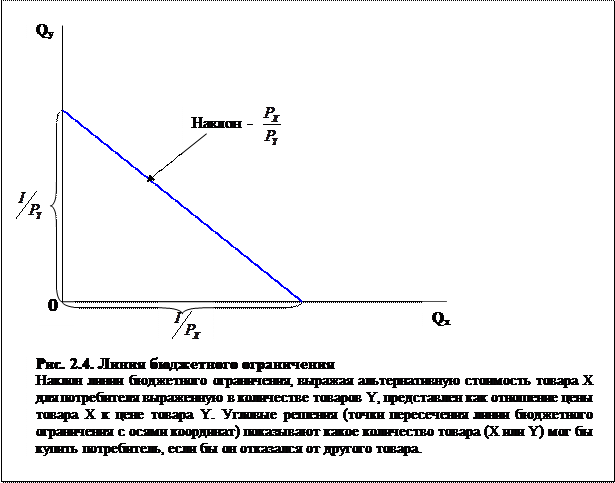товара мог бы купить потребитель, если бы полностью отказался от другого товара, и получили название угловых решений. Для оси 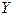это точка будет на расстоянии 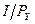от начала координат, для оси 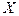– на расстоянии 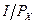от начала координат. Графическое изображение этой кривой получило название линии бюджетного ограничения или бюджетной линии (budget line).

Вообще, удобнее представить эту линейную функцию в традиционной форме, когда в левой ее части располагается переменная, которую обычно отображают на вертикальной оси, а в правой – все остальное:

.

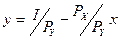Теперь свободный член (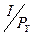) выражает расстояние от начала координат до точки, в которой наша кривая пересекает вертикальную ось, а коэффициент при 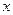– это тангенс угла ее наклона. Умножение этого коэффициента на -1 дает соотношение цен 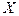и 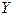. Чем круче бюджетная линия, тем больше отношение цены 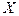к цене 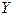и, следовательно, тем большим количеством товара 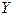должен пожертвовать, чтобы получить дополнительную единицу товара 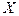. Фактически отношение 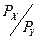показывает, от какого количества товара 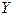должен отказаться потребитель при полном расходовании своего бюджета, если он пожелает приобрести дополнительную единицу товара 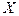, то есть не что иное, как альтернативную стоимость блага X, выраженную в количестве блага .

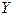Бюджетное ограничение может меняться при изменении составляющих его параметров. Так, изменение дохода приведет к параллельному сдвигу линии бюджетного ограничения вверх, если доход увеличивается, или вниз, если доход уменьшается. Изменение цен, по которым потребитель покупает товары, приведет к тому, что угловое решение сдвинется по оси, соответствующей товару, цена которого изменилась. Сдвинется влево при повышении цены и вправо при снижении цены. Пропорциональное изменение цен обоих товаров приведет к изменениям, аналогичным тем, которые имеют место при изменении дохода.

Date: 2015-06-08; view: 786; Нарушение авторских прав