Поиск оптимальной трассы на неориентированном графе

1. Процедуру поиска оптимальной трассы покажем на примере неразветвляющего трубопровода. Имеем сеть, множество дуг которой образуют неориентированный граф, формальные па­раметры которого обозначим: D — одномерный массив инфор­мации о сети, состоящей из последовательностей трех элемен­тов, характеризующих одну дугу: N_HАЧ — номер узла начала дуги, N_koh — номер узла конца дуги, до — критерий оптималь­ности, IPB —номер узла начальной точки сети, IPE — номер узла конечной точки сети, NT — массив номеров в массиве D с информацией о дугах дерева; ОРТ — массив номеров элемен­тов в массиве D с информацией о дугах кратчайшего пути.

Поиск производится следующим образом.

В массиве информации D отыскиваются дуги, вершиной ко­торых является точка, определенная в исходных данных, как начальная. Для этой цели организуются вложенные циклы, ко­торые обеспечивают поиск любой дуги, вершиной которой яв­ляется заданная точка независимо от ориентации дуги (после­довательности записи элементов массива D_i, D_{i +1}, инцидентных дуге вершин). Информация о найденной дуге заносится в мас­сивы Р и ND, где Р — массив значений длины всей цепи от на­чального узла до рассматриваемого; ND — номер элемента мас­сива Р, содержащего информацию о рассматриваемой дуге. Запоминаются значение длины цепи для рассмотренного узла, номер соответствующего элемента в массиве Р. Для указания последнего значащего элемента P_(j) в массиве Р элементу P_{(j+ 1)} присваивается заведомо большое и нереальное при расчетах значение. Следующие циклы ограничены именно этим элементом массива. В массиве Р исключаются большие из пу­тей достижения одного узла, если такие имеются. Кроме того, определяется элемент справочного массива, содержащий мини­мальное значение длины цепи. Рассмотренная дуга включается в состав ветвей дерева и инцидентный ей узел становится уз­лом дальнейшего развития поиска. Цикл по j продолжается до тех пор, пока не встретится узел, определенный в исходных данных как конечный. Если дерево построено (число его вет­вей KNT), то на нем фиксируется кратчайший путь. Результа­том работы процедуры, выходными формальными параметрами является массив NT номеров элементов массива D —дуг де­рева и массив ОРТ — значений номеров узлов следования кратчайшего пути на графе.

2. В предыдущем пункте рассмотрен метод поиска кратчай­шего пути между двумя точками неориентированного графа. Этот метод эффективен при поиске кратчайшего пути на сети с большим числом дуг. Однако его эффективность существенно снижается в задачах поиска точек разветвления систем трубо­проводов, поскольку во всех возникающих ситуациях много­кратно повторяются процессы поиска кратчайшего пути между двумя точками. С этой точки зрения представляет интерес ме­тод поиска многополюсных кратчайших цепей между всеми парами узлов сети. Он обеспечивает быстродействие при мно­гократном выборе кратчайшего пути между парами узлов, однако из-за необходимости хранения в памяти ЭВМ матрицы результатов он ограничен по объему информации о сети.

Рассмотрим алгоритм поиска многополюсных кратчайших цепей.

На графе возможных путей развития лишь некоторые дуги Aij являются кратчайшими цепями из N_i в n _j, они принадле­жат дереву графа. Предположим, что известна кратчайшая цепь из узла N_s в узел Nt. Тогда эта цепь должна состоять только из дуг дерева, в противном случае она не будет крат­чайшей. Если теперь ввести дугу A_st с длиной, равной длине рассматриваемой цепи N_s — N_t, то эта дуга A_si будет также принадлежать дереву. Задача нахождения кратчайших цепей между -всеми парами узлов реализуется добавлением дуги де­рева (если таких дуг в цепи не было) между всеми парами узлов.

Рассмотрим операцию получения дуги дерева относительно узла n _j

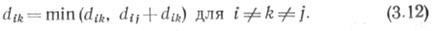
При этом сравнивается длина d_ik дуги А_ik и длина цепи N_i— nj — N_h. Затем длине дуги A_ih присваивается значение d_ij + d_jk при условии d_ik>d_ij + d_jk. Если выполнить эту операцию после­довательно для каждого узла Nj(j=1, 2,..., п), то полученные в результате значения Dih будут длинами кратчайших цепей между всеми парами узлов.

По мере последовательного выполнения операции (3.12) за­полняется справочная таблица. Элемент (i, k) этой таблицы, стоящий на пересечении i'-й строки и k-ro столбца, полагаем равным k. После выполнения операции (3.12) элемент указы­вает первый промежуточный узел в кратчайшей цепи между Ni и Nh, если такой узел существует, в противном случае эле­мент (i, k) равен k.

Таким образом

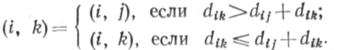
Для того чтобы найти кратчайшую цепь из N_s в N_t, no спра­вочной таблице сначала отыскивается элемент s, t = k, который означает, что узел Nh является первым промежуточным узлом в кратчайшей цепи из N_S в N_t. Затем находится элемент (k, t), который указывает первый промежуточный узел в кратчайшей цепи из N_h в N_t. Этот процесс продолжается до тех пор, пока не будет найден элемент (i, t)=T, который означает, что най­дены все узлы, входящие в кратчайшую цепь из N_S в N_t, а именно N_S N_k,..., n _i, N_t.

Если при выборе оптимальных трасс газопроводов и их paз­ветвлений используется неориентированная сеть произвольной конфигурации, то для поиска многополюсных кратчайших це­пей на такой сети допустимо использовать симметричные мат­рицы исходных данных, длин кратчайших путей и узлов про­хождения кратчайших путей. Это позволяет хранить лишь по­ловину исходной и выходной информации, что существенно повышает эффективность применения рассматриваемого метода и его реализуемость

на ЭВМ. Следует отметить, что метод позволяет также сохранять произвольность распределения пометок графа.

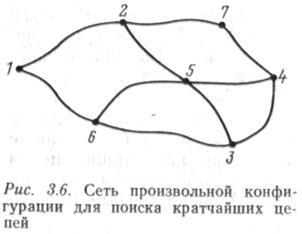
Рассмотрим работу алго­ритма нахождения кратчай­ших цепей между всеми па­рами узлов (рис. 3.6). Усло­вимся, что дуги графа не ори­ентированы. Длины дуг отрез­ков сети заносятся в таблицу. Выполняем операции (3.12) (для j=1), заключающиеся в том, что определяются все элементы табл. 3.2, не лежащие в первой строке и в первом столбце. Длины кратчайших цепей заносятся в табл. 3.3, а узлы прохождения пути — в табл. 3.4;

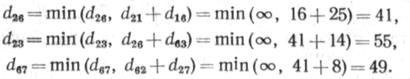
Величины d₂₆ и d₅₆ своего значения не изменили.

Для /=2 также выполняется операция (3.12), определяю­щая все элементы теперь уже табл. 3,3, не лежащие во второй строке и втором столбце, так как при этом используются ре­зультаты вычислений при j=1;

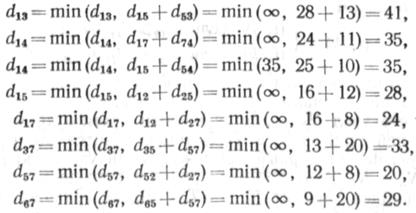
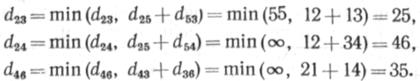
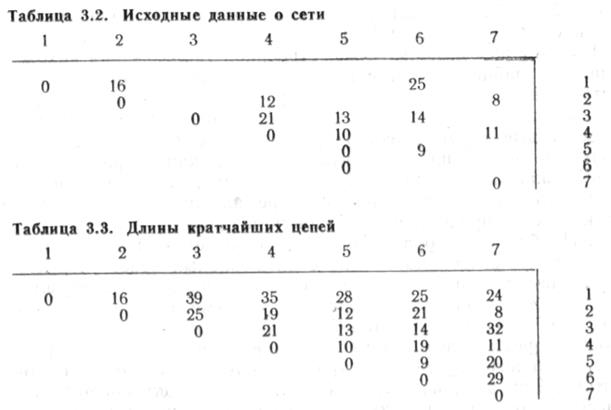
Величины d₁₄, d₄₇, d₅₆ своего значения не изменили. Для j = 3:

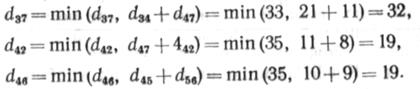
Величины d₅₇ , d₆₇ своего значения не изменили. Для j = 5:

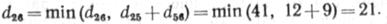
Величины d₁₃,d₁₄, d₁₆,d₁₇, d₂₃, d₂₄, d₃₇ , d₆₇ своего значения не из­менили.

Результатом вычислений являются табл. 3.3 длин кратчай­ших цепей и справочная табл. 3.4, с помощью которой опреде­ляются узлы, входящие в кратчайшие цепи. Пусть, например, необходимо найти кратчайшую цепь из N₁ в N₄. Тогда по табл. 3.4 сначала находим элемент (1,4) =7. Затем находим

(1,7) =2 и (1,2) = 1. Следовательно, кратчайшая цепь из N₁ в jV₄ проходит через узлы N₂ и N₇

Таким образом, пользуясь построенной табл. 3.4 для нахож­дения кратчайших цепей между любыми двумя парами узлов, достаточно выполнить лишь некоторое число операций сравне­ния, равное числу дуг в искомом кратчайшем пути. Это дает существенные преимущества рассматриваемому методу, по­скольку в предыдущих алгоритмах для отыскания кратчайшего пути из какой-либо точки необходимо строить дерево относи­тельно этой точки, что при переборе начальных и конечных точек на сети представляет трудоемкий процесс.

3. Проблема выбора оптимального разветвления трубопро­вода состоит не только в поиске оптимальных трасс участков между двумя пунктами, но и в определении места оптималь­ного разветвления при отборе или притоке перекачиваемого продукта. Для решения данной задачи будем исходить из сле­дующих предпосылок. Сеточная модель местности представ­ляет собой возможные пути проложения трассы и отвода или притока. При этом не делается различий для дуг проложения трассы и отвода (притока)—каждая дуга может принадле­жать как основной магистрали, так и отводу. Естественно, что дуги сети не ориентированы. Точка разветвления находится в одном из узлов сети. В противном случае постановка не со­ответствует основной предпосылке решаемой задачи — любые пересечения возможных путей проложения трассы являются узлами сети. Конфигурацию разветвления удобно рассматри­вать как три независимых участка, сходящихся в одной точке. При этом концевые точки каждого из участков являются ис­ходными данными.

В зависимости от технологической схемы транспорта газа возможны сочетания вариантов диаметров трубопроводов раз­ветвленной системы (рис. 3.7):

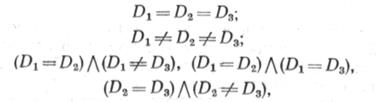
где d₁ , D₂ , D₃ — диаметры трубопроводов соответственно пер­вого, второго и третьего участков.

Алгоритмы поиска оптимального разветвления для перечисленных вариантов различны. Рассмотрим наиболее простой слу­чай, когда все диаметры трубопровода равны (D₁ D₂, D₃). Сеть представляет собой помеченный неориентированный граф G(A, N) (рис. 3.8). В общем случае каждая вершина множе­ства вершин N_i Е G(А, N) может рассматриваться как воз­можная точка разветвления N_si системы, а кратчайшие пути для трех участков находятся на ветвях дерева, построенного относительно этой точки разветвления в конечные точки участков N_tj(j=l, 2, 3). Относительно

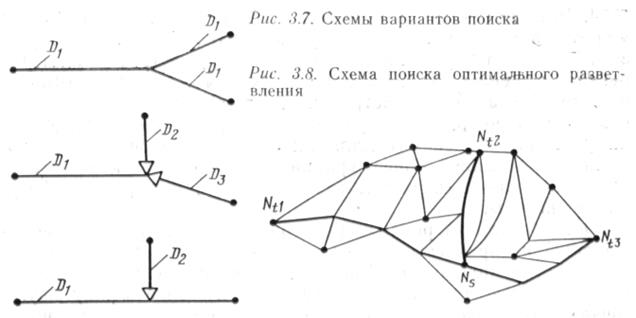
вершин N_si по методу поиска кратчайшего пути на неориентированном графе осуществляется поиск кратчайшего пути в каждую из вершин N_tj(j=\, 2, 3), т. е. строится дерево графа относительно вершины N_s. Постро­енное дерево позволяет отыскать кратчайшие цепи на участ­ках Л/.„, Ntj(j=l, 2, 3) и определить их длину L_tj или значение другого критерия оптимальности. Суммарный кратчайший путь системы

Осуществляемый перебор вершин графа в заданной области разветвления позволяет отыскать вершину, удовлетворяющую условию

Выбранная таким образом точка разветвления будет оптималь­ной относительно заданного критерия. Если точка разветвления совпала с одним из узлов Ntj(j=l, 2, 3), т. е. отвод «вырожда­ется», то рассматриваются два участка газопровода.

Рассмотрим алгоритм поиска оптимального разветвления системы для случая, если диаметры всех трех участков раз­личны. В этом случае для каждого участка строятся три графа G\(A\, N), С₂(Л₂, N), G₃(A₃, N), соответствующие исходной сети. Для этих графов существует взаимно однозначное соот­ветствие между А}, Л₂, А₃, сохраняющее отношения инцидент­ности и распределения пометок. Следовательно, рассмотренные графы изоморфны. Для графа G\(A\, N) и отдельно для графа 0₂(Л₂, N) строится дерево при значениях критерия оптималь­ности, соответствующих участку М,,-, Nti, и отыскивается крат­чайшая цепь на графе между этими точками, а также суммар­ное значение критерия оптимальности для найденного пути.

4. Разработанные алгоритмы поиска оптимальной трассы между двумя точками и алгоритм поиска оптимального раз­ветвления системы магистрального газопровода позволяют пе­рейти к решению более сложной проблемы — выбору оптималь­ных трасс системы магистральных трубопроводов со многими отводами. Проблему выбора сложных трасс можно разделить на 2 задачи: поиск оптимальных трасс газопроводов с отво­дами при заданной конфигурации системы и поиск оптималь­ных трасс сложных систем газопроводов с выбором конфигу­рации системы.

Остановимся на реализации первой задачи, применив моди­фикацию иерархического метода оптимизации магистральных нефтепродуктопроводов. При выборе трасс сверхпротяженных трубопроводов длиной 2000—2500 км и более между двумя точками сеть разбивается на ряд фрагментов с граничными группами узлов. Эти группы рассматриваются как макро­группы, если под макродугами подразумевать участки опти­мальной трассы между двумя смежными граничными участ­ками. Расстояние между граничными группами рекомендуется принимать 400—700 км. Используя суперпозицию изложенного метода, можно рассчитывать трассы практически любой про­тяженности.

Задана неориентированная сеть произвольной конфигура­ции с определенными начальными и конечными узлами трассы, а также конечными точками отводов (притоков) на сети и ориентировочно определенными областями их подключения к основной магистрали трассы (рис. 3.9). Сеть представляет собой неориентированный граф G(V, N), который разобьем на подграфы G(Vh, N), а множество вершин на независимые под­множества V_k(k=\, 2,..., п), где п —число отводов. При этом необходимо выполнение условия V\(] V^nVsH, • • • • ПУ_пз=0, т. е. подмножества графа не должны пересекаться. Кроме того, в каждом из подграфов Gk(Vk, N) должно находиться не бо­лее одного разветвления. Вершины N_v, инцидентные обоим со­седним подмножествам, назовем соединяющими. Числом вер­шинного соединения /(Vh) подмножества V_ft назовем число со­единяющих вершин с подмножеством ул+ь будем говорить, что подмножества V\ и Vh+\ вершинно соединены. Аналогичные по­нятия существуют и для реберного соединения подграфов. Сле­довательно, к условию разбиения графа добавим еще одно: p(Vk, V\+i)=0, т. е. отсутствие реберного соединения подмно­жеств. Такой граф называется сепарабельным.

Таким образом, в результате разбиения графа на подграфы имеем некоторую конфигурацию системы, состоящую из вер­шинных соединений подмножеств (рис. 3.10). Очевидно, что каждая пара сочетаний Ы_пн, Л/ль+i вершинных соединений, от­носящихся к одному подмножеству, представляет собой рас­четный вариант, для которого возможно отыскание оптималь­ной точки разветвления либо оптимальной трассы между двумя точками.

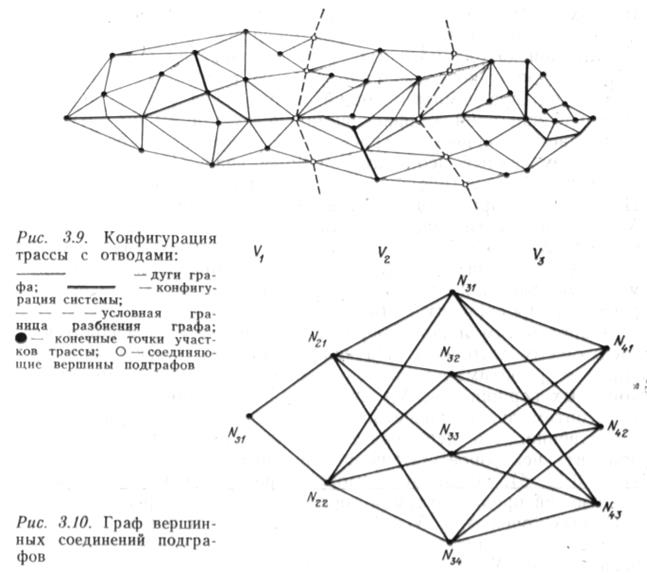
Напомним, что по условию разбиения в подграфе должно находиться не более одного разветвления системы. Это обусловлено тем, что разработанный математический и про­граммный аппарат позволит оптимизировать именно такой ва­риант. В случае, если разветвление для подмножества V/, от­сутствует, то кратчайший путь находится между двумя точками Nnh, N_n+t{,h(k=l, 2,..., l(Vk), где l(V_k) — число вершинных разбиений).

После выполнения расчетов для каждого из подмножеств строится граф вершинных соединений G(Vk, N„1,), поиск крат­чайшего пути между двумя точками которого не представляет особого труда.

Ввиду простоты алгоритма и наличия математического и программного аппарата поиска оптимальной трассы и опти­мальной точки разветвления оптимизация трассы газопровода с отводами при заданной конфигурации системы выполняется путем последовательной реализации предложенных этапов. Следует отметить, что этот путь является наиболее надежным и реализуемым при оптимизации сложных систем газопрово­дов, поскольку в случае появления ошибок исходной информации их локализация значительно упрощается, что приводит к увеличению надежности работы программ.

Для поиска оптимальных трасс сложных систем газопрово­дов с выбором конфигурации системы разработан итерацион­ный метод, предусматривающий оптимальное уточнение перво­начально заданной конфигурации системы и выбор оптималь­ных участков основной трассы и отводов. Сеть представляет собой помеченный неориентированный граф G(V, N).

Зададим ориентировочную конфигурацию системы на сети. Исходной информацией будут номера узлов начала nu и конца Nt2 основной магистрали, конечные точки отводов или притоков на сети Л/₍ь(й = 3, 4,..., п, где п — число отводов), диаметры трубопроводов на участках. Кроме того, произвольно зададим узлы подключения отводов (притоков) к магистрали, т.е. точки разветвления системы N_sk(k=l, 2,..., п).

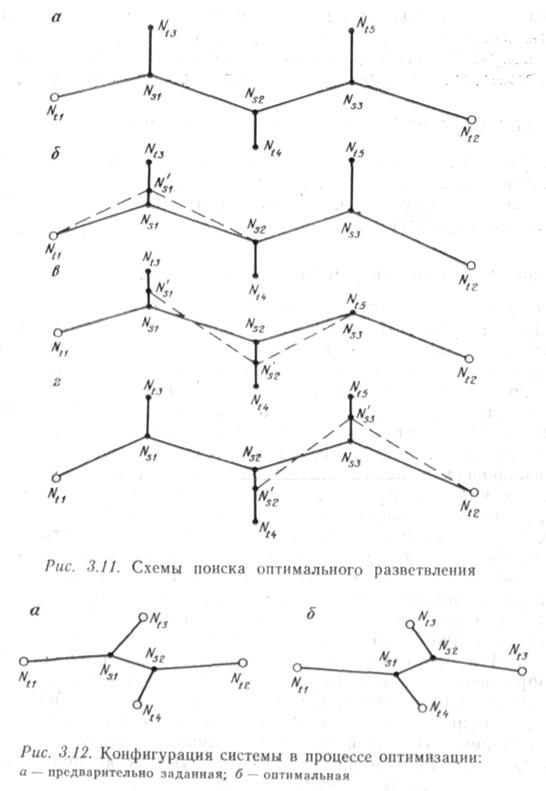
Выбор оптимальной конфигурации системы производится тю следующему алгоритму. На графе G(V, N) отыскивается вер­шина yV.,i оптимального разветвления системы относительно конечных вершин N_t\, Nt2, Ntz по уже описанному методу по­иска оптимального разветвления трассы с отводом (рис. 3.11, а). Естественно, что первоначально заданный узел разветвления получит некоторое смещение и перейдет в вершину /V'_sl (рис. 3.11, б). После этого можно приступить к рассмотрению следующей предполагаемой точки разветвления, решив систему конечных точек ЛГ,,₂, nh, М>з относительно точки Af,,₂. Следую­щим этапом решается система N'_K2, N_t5, N12 относительно точки разветвления N_s3 (рис. 3.11, 0). Откорректированная таким об­разом система разветвлений становится исходной (базовой) для следующего цикла последовательных решений (рис. 3.11, г). Процесс продолжается до момента сходимости, т.е. до тех пор, пока итерации решений поиска разветвления системы не при­ведут к постоянным координатам узлов разветвления.

Несколько усложним предполагаемый алгоритм с целью выбора оптимальных трасс и конфигураций системы. Предпо­ложим для простоты изложения, что все диаметры системы ма­гистрального трубопровода Nt\Ns\, Л^₂Л^₂ и отводов N_x]Ni;\, N*tNtt (рис. 3.12, а) одинаковы. При поиске оптимального раз­ветвления системы Nt\N& относительно точки разветвления N_x\ строим дерево не для определенной конечной точки отвода /V₍₃, а для ближайшей с точки зрения алгоритма построения де­рева. Таким образом, с искомой точкой разветвления Л^ мо­жет соединиться не предварительно заданная вершина #<₃, а более целесообразная с точки зрения данного алгоритма вершина N_t* (рис. 3.12, б). Безусловно, на следующих итера­циях процесса ситуация может измениться и «ближайшей» ока­жется опять-таки, вершина /V₍₄- Таким образом, на каждом шаге итерационного процесса осуществляется не только выбор оптимальных на данной итерации точек разветвления системы, а и наиболее целесообразная ее конфигурация. Этот алгоритм реализуется и для

системы с трубопроводами различных диа­метров.

Проведение практических расчетов показало, что анализ исходной информации занимает в 2—2,5 раза больше машин­ного времени, чем непосредственно выбор оптимальной трассы. Однако следует учитывать, что одного-двух расчетов в режиме поиска ошибок оказывается достаточно для выявления, лока­лизации и последующей корректировки искажений информа­ции. Произвольное задание сети, простота и наглядность опи­сания информации о дугах, наличие развитой системы диагностнки ошибок позволяют уменьшить непроизводительные за­траты машинного времени, сократить сроки проведения расче­тов, получить качественный исходный материал и, таким обра­зом, повысить уровень достоверности проводимых расчетов.

Date: 2015-06-07; view: 1226; Нарушение авторских прав